第3章《位置与坐标》【挑战满分】2022-2023学年数学八上阶段性复习精选精练(北师大版 含解析)
文档属性
| 名称 | 第3章《位置与坐标》【挑战满分】2022-2023学年数学八上阶段性复习精选精练(北师大版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 889.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-29 21:34:39 | ||
图片预览

文档简介
第3章《位置与坐标》
一、单选题
1.点A(5,-4)在第几象限( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列各点在第二象限的是
A., B. C. D.
3.平面直角坐标系中,点P(﹣2,3)关于x轴对称的点的坐标为( )
A.(2,﹣3) B.(﹣2,3) C.(﹣2,﹣3) D.(2,3)
4.若点在第二象限,则点在()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如果点与关于轴对称,则,的值分别为( )
A., B.,
C., D.,
6.如图是战机在空中展示的轴对称队形.以飞机B,C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(40,a),则飞机D的坐标为( )
A. B. C. D.
7.如果第二列第一行用有序数对(2,1)表示,那么数对(3,6)和(3,4)表示的位置是( )
A.同一行 B.同一列 C.同行同列 D.不同行不同列
8.如图,笑脸盖住的点的坐标可能为( )
A. B. C. D.
9.已知平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )
A.﹣3 B.﹣5 C.1或﹣3 D.1或﹣5
10.昌平公园建成于1990年,公园内有一个占地10000平方米的静明湖,另外建有弘文阁、碑亭、文节亭、诗田亭、逸步桥、牌楼等园林景观及古建筑.如图,分别以正东、正北方向为x轴、y轴建立平面直角坐标系,如果表示文节亭的点的坐标为(2,0),表示园中园的点的坐标为(-1,2),则表示弘文阁所在的点的坐标为( )
A.(-2,-3) B.(-2,-2)
C.(-3,-3) D.(-3,-4)
二、填空题
11.在平面直角坐标系中,点 P( 2,1)关于 x 轴的对称点的坐标为_____
12.点(3,0)关于y轴对称的点的坐标是_______
13.点P关于x轴对称点是,点P关于y轴对称点是,则__________.
14.点A(3m﹣1,2m)位于第一、三象限的角平分线上,则m=_____.
15.在平面直角坐标系中,点M(a,b)与点N(3,﹣1)关于x轴对称,则的值是_____.
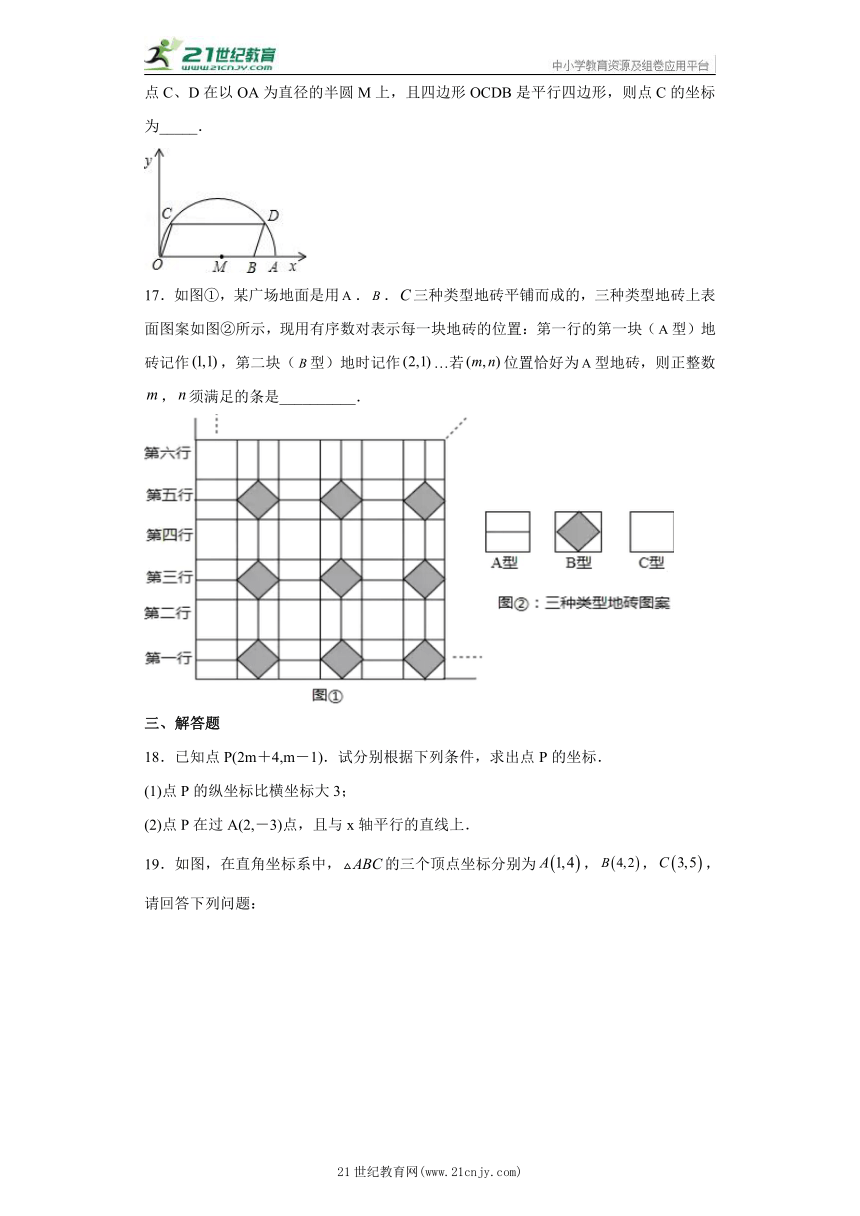
16.如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为_____.
17.如图①,某广场地面是用..三种类型地砖平铺而成的,三种类型地砖上表面图案如图②所示,现用有序数对表示每一块地砖的位置:第一行的第一块(型)地砖记作,第二块(型)地时记作…若位置恰好为型地砖,则正整数,须满足的条是__________.
三、解答题
18.已知点P(2m+4,m-1).试分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,-3)点,且与x轴平行的直线上.
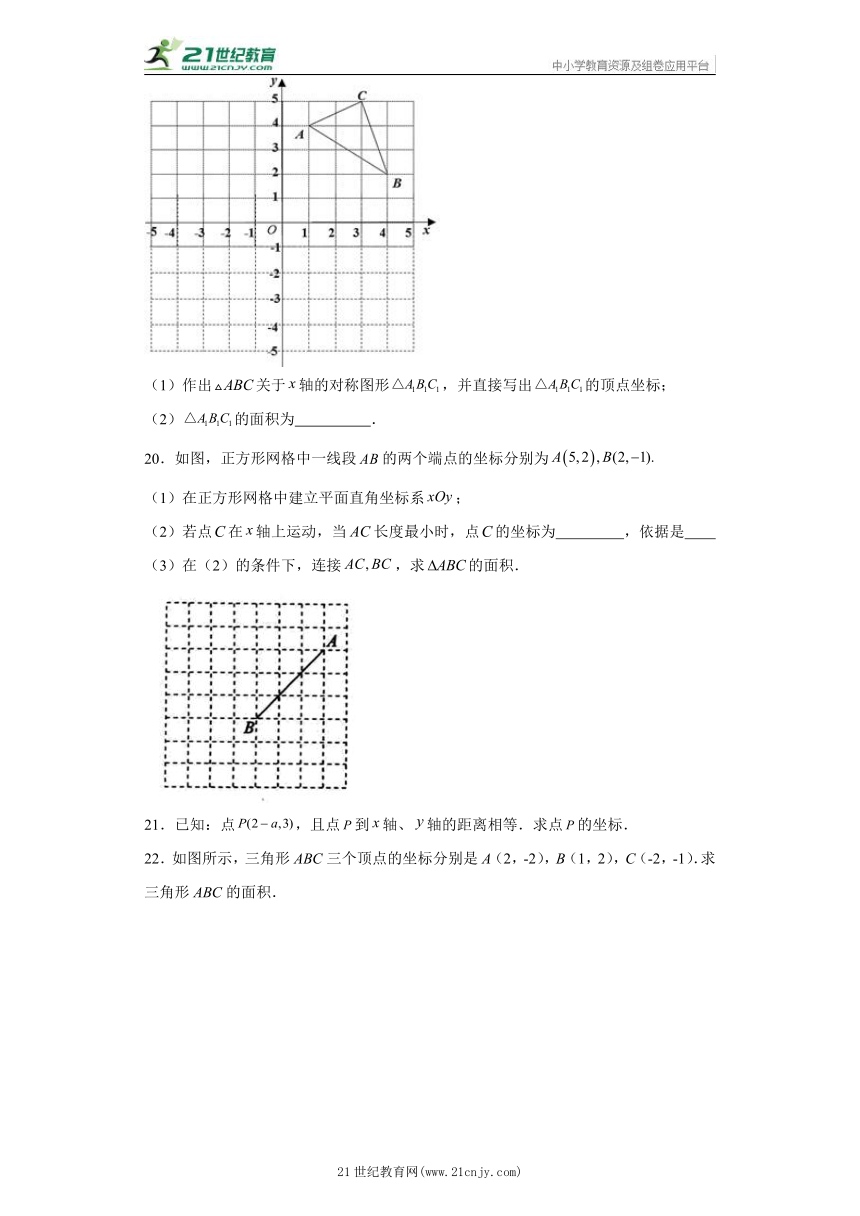
19.如图,在直角坐标系中,的三个顶点坐标分别为,,,请回答下列问题:
(1)作出关于轴的对称图形,并直接写出的顶点坐标;
(2)的面积为 .
20.如图,正方形网格中一线段的两个端点的坐标分别为
(1)在正方形网格中建立平面直角坐标系;
(2)若点在轴上运动,当长度最小时,点的坐标为 ,依据是
(3)在(2)的条件下,连接,求的面积.
21.已知:点,且点到轴、轴的距离相等.求点的坐标.
22.如图所示,三角形ABC三个顶点的坐标分别是A(2,-2),B(1,2),C(-2,-1).求三角形ABC的面积.
23.已知点,解答下列各题.
(1)点P在x轴上,求出点P的坐标.
(2)点Q的坐标为,直线轴;求出点P的坐标.
(3)若点P在第二象限,且它到x轴、y轴的距离相等,求的值.
参考答案:
1.D
【解析】
【分析】
四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
【详解】
解:∵点A的横坐标为正数、纵坐标为负数,
∴点A(5,-4)在第四象限,
故选D.
【点睛】
本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键.
2.B
【解析】
【分析】
根据各象限内点的坐标特征对各选项分析判断利用排除法求解.
【详解】
、,在轴上,故本选项不合题意;
、在第二象限,故本选项符合题意;
、在轴上,故本选项不合题意;
、在第四象限,故本选项不合题意.
答案:B.
【点睛】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
3.C
【解析】
【分析】
根据关于x轴对称点的坐标特点即可求解.
【详解】
解:∵关于x轴对称点的坐标特点:横坐标相同,纵坐标互为相反数,
∴点P(﹣2,3)关于x轴的对称点坐标是(﹣2,﹣3),
故答选:C.
【点睛】
此题主要考查关于x轴对称的点,解题的关键是熟知关于x轴对称点的坐标特点.
4.C
【解析】
【分析】
根据第二象限内的点的横坐标小于零,纵坐标大于零,可得关于a、b的不等式,再根据不等式的性质,可得B点的坐标符号.
【详解】
解:根据题意知,
解得:a<﹣1,b>2,
则a-3<0,1-b<0,
∴点在第三象限,
故选:C.
【点睛】
本题考查了点的坐标,利用第二象限内点的横坐标小于零,纵坐标大于零得出不等式,又利用不等式的性质得出B点的坐标符号是解题关键.
5.A
【解析】
【分析】
根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.即点P(x,y)关于y轴的对称点P′的坐标是(-x,y),进而得出答案.
【详解】
解:∵点P(-m,3)与点Q(-5,n)关于y轴对称,
∴m=-5,n=3,
故选:A.
【点睛】
此题主要考查了关于y轴对称点的性质,正确记忆关于坐标轴对称点的性质是解题关键.
6.B
【解析】
【分析】
直接利用关于y轴对称,纵坐标相同,横坐标互为相反数,进而得出答案.
【详解】
解:根据题意,点E与点D关于y轴对称,
∵飞机E的坐标为(40,a),
∴飞机D的坐标为(-40,a),
故选:B.
【点睛】
此题主要考查了关于y轴对称点的性质,正确记忆横纵坐标的符号关系是解题关键.
7.B
【解析】
【分析】
数对中第一个数字表示列数,第二个数字表示行数,据此可作出判断.
【详解】
解:第二列第一行用数对(2,1)表示,则数对(3,6)表示第三列,第六行,数对(3,4)表示表示第三列,第四行.所以数对(3,6)和(3,4)表示的位置是同一列不同行.
故选:B.
【点睛】
本题主要考查了坐标确定位置,一般用数对表示点位置的方法是第一个数字表示列,第二个数字表示行,也有例外,具体题要根据已知条件确定.
8.B
【解析】
【分析】
根据图形得出笑脸的位置,进而得出答案.
【详解】
解:由图形可得:笑脸盖住的点在第二象限,故笑脸盖住的点的坐标可能为( 6,3).
故选:B.
【点睛】
此题主要考查了点的坐标,得出笑脸的横纵坐标符号是解题关键.
9.A
【解析】
【分析】
根据点A(a+2,4)和B(3,2a+2)到x轴的距离相等,得到4=|2a+2|,即可解答.
【详解】
解:∵点A(a+2,4)和B(3,2a+2)到x轴的距离相等,
∴4=|2a+2|,a+2≠3,
解得:a= 3,
故选A.
【点睛】
考查点的坐标的相关知识;用到的知识点为:到x轴和y轴的距离相等的点的横纵坐标相等或互为相反数.
10.B
【解析】
【分析】
直接利用文节亭的点的坐标为(2,0),进而得出原点位置进而得出答案.
【详解】
如图所示:
弘文阁所在的点的坐标为:(-2,-2).
故选:B.
【点睛】
此题主要考查了坐标确定位置,正确得出原点位置是解题关键.
11.(2,1)
【解析】
【分析】
根据与x 轴对称的点的性质,求出对称点的坐标即可.
【详解】
∵对称点与点 P( 2,1)关于 x 轴对称
∴保持横坐标不变,纵坐标取相反数
∴对称点的坐标为
故答案为:.
【点睛】
本题考查了关于x 轴的对称点的坐标问题,掌握与x 轴对称的点的性质是解题的关键.
12.(-3,0)
【解析】
【分析】
根据平面直角坐标系中两个关于坐标轴成轴对称的点的坐标特点,直接用假设法设出相关点即可.
【详解】
解:点(m,n)关于y轴对称点的坐标(-m,n),
所以点(3,0)关于y轴对称的点的坐标为(-3,0).
故答案为:(-3,0).
【点睛】
本题考查平面直角坐标系点的对称性质:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
13.1
【解析】
【分析】
根据关于坐标轴的对称点的坐标特征,求出a,b的值,即可求解.
【详解】
∵点P关于x轴对称点是,
∴P(a,-2),
∵点P关于y轴对称点是,
∴b=-2,a=3,
∴1,
故答案是:1.
【点睛】
本题主要考查关于坐标轴对称的点的坐标特征,熟练掌握“关于x轴对称的两点,横坐标相等,纵坐标互为相反数;关于y轴对称的两点,横坐标互为相反数,纵坐标相等”是解题的关键.
14.1
【解析】
【分析】
根据第一、三象限角平分线上点的坐标特征得到得3m﹣1=2m,然后解关于m的一次方程即可.
【详解】
解:∵点A(3m﹣1,2m)在第一、三象限的角平分线上,
∴3m﹣1=2m,
解得:m=1.
故答案为:1
【点睛】
此题考查象限及点的坐标的有关性质,解题关键在于掌握其定义列出方程.
15.1
【解析】
【分析】
根据关于x轴对称的两点的横坐标相同,纵坐标互为相反数求得a、b的值即可求得答案.
【详解】
解:在直角坐标系中,关于x轴对称的两点,横坐标相同,纵坐标互为相反数,
∵点M(a,b)与点N(3,﹣1)关于x轴对称,
∴a=3,b=1,
∴=1,
故答案为:1.
【点睛】
本题考查了关于x轴对称的点的坐标特征,熟练掌握关于坐标轴对称的点的坐标特征是解题的关键.
16.(2,6)
【解析】
【分析】
此题涉及的知识点是平面直角坐标系图像性质的综合应用.过点M作MF⊥CD于F,过C作CE⊥OA于E,在Rt△CMF中,根据勾股定理即可求得MF与EM,进而就可求得OE,CE的长,从而求得C的坐标.
【详解】
∵四边形OCDB是平行四边形,点B的坐标为(16,0),
CD∥OA,CD=OB=16,
过点M作MF⊥CD于F,则
过C作CE⊥OA于E,
∵A(20,0),
∴OA=20,OM=10,
∴OE=OM ME=OM CF=10 8=2,
连接MC,
∴在Rt△CMF中,
∴点C的坐标为(2,6).
故答案为(2,6).
【点睛】
此题重点考察学生对坐标与图形性质的实际应用,勾股定理,注意数形结合思想在解题的关键.
17.m、n同为奇数或m、n同为偶数
【解析】
【分析】
几何图形,观察A型地砖的位置得到当列数为奇数时,行数也为奇数,当列数为偶数,行数也为偶数的,从而得到m、n满足的条件.
【详解】
解:观察图形,A型地砖在列数为奇数,行数也为奇数的位置上或列数为偶数,行数也为偶数的位置上,
若用(m,n)位置恰好为A型地砖,正整数m,n须满足的条件为m、n同为奇数或m、n同为偶数,
故答案为:m、n同为奇数或m、n同为偶数.
【点睛】
本题考查了坐标表示位置:通过类比点的坐标考查解决实际问题的能力和阅读理解能力.分析图形,寻找规律是关键.
18.(1)点P(-12,-9)(2)P(0,-3)
【解析】
【详解】
试题分析:(1)根据横纵坐标的大小关系得出m﹣1﹣(2m+4)=3,即可得出m的值,进而得出P点坐标;
(2)根据平行于x轴点的坐标性质得出m﹣1=﹣3,进而得出m的值,进而得出P点坐标.
解:(1)∵点P(2m+4,m﹣1),点P的纵坐标比横坐标大3,
∴m﹣1﹣(2m+4)=3,
解得:m=﹣8,
∴2m+4=﹣12,m﹣1=﹣9,
∴点P的坐标为:(﹣12,﹣9);
(2)∵点P在过A(2,﹣3)点,且与x轴平行的直线上,
∴m﹣1=﹣3,
解得:m=﹣2,
∴2m+4=0,
∴P点坐标为:(0,﹣3).
19.(1)图见解析,,,;(2).
【解析】
【分析】
(1)利用轴对称的性质即可画出,再根据坐标系中所画出的三角形即可写出其顶点坐标.
(2)如图利用割补法即可求出的面积.
【详解】
(1)如图,即为所求,由图可知,,.
.
(2)如图取E(1,-2),F(1,-5),G(4,-5),分别连接E、、G、F,由图可知四边形EGF为正方形.
所以,
即.
故答案为:.
【点睛】
本题考查利用轴对称作图,利用轴对称的性质找出对称点的位置是解决问题的关键.
20.(1)见解析;(2)(5,0),垂线段最短;(3)3
【解析】
【分析】
(1)根据点A和点B的坐标找到原点位置,并建立坐标系即可;
(2)根据垂线段最短的基本事实,过A作x轴的垂线,垂足为C,求出C坐标即可;
(3)以AC为底,计算△ABC的面积,利用公式计算结果即可.
【详解】
(1)如图所示:
(2),垂线段最短.
(3)如图所示:
所以的面积为.
【点睛】
考查平面直角坐标系内坐标以及几何的一些问题,学生要熟练掌握平面直角坐标系的相关知识点,并结合三角形等几何问题解出本题.
21.点的坐标或
【解析】
【分析】
根据到两坐标的距离相等,可得关于a的方程,根据解方程,可得答案.
【详解】
点到轴、轴的距离相等.
,
,
或,
点的坐标或.
【点睛】
本题考查了点的坐标,利用到两坐标的距离相等得出关于a的方程是解题关键.
22.三角形ABC的面积为7.5.
【解析】
【分析】
利用割补法即可求解.
【详解】
过点A,C分别作平行于y轴的直线,过点A,B分别作平行于x轴的直线,它们的交点为D,E,F,得到正方形ADEF,则该正方形的面积为4×4=16.
三角形ABD、三角形BCE、三角形ACF的面积分别是:,,.
所以三角形ABC的面积为16-2-4.5-2=7.5.
【点睛】
此题主要考查坐标与图形,解题的关键是熟知割补法的运用.
23.(1);(2);(3)2021
【解析】
【分析】
(1)根据x轴上点的坐标特征:纵坐标为0,列出方程即可求出结论;
(2)根据与y轴平行的直线上两点坐标关系:横坐标相等、纵坐标不相等即可求出结论;
(3)根据题意可得:点P的横纵坐标互为相反数,从而求出a的值,即可求出结论.
【详解】
解:(1)若点P在x轴上,
∴a+5=0
解得:a=-5
∴;
(2)∵点Q的坐标为,直线轴
∴
解得:a=3
∴;
(3)∵点P在第二象限,且它到x轴、y轴的距离相等
∴
解得:a=-1
∴==2021
【点睛】
此题考查的是根据题意,求点的坐标,掌握x轴上点的坐标特征、与y轴平行的直线上两点坐标关系和点到x轴、y轴的距离与坐标关系是解题关键.
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
一、单选题
1.点A(5,-4)在第几象限( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列各点在第二象限的是
A., B. C. D.
3.平面直角坐标系中,点P(﹣2,3)关于x轴对称的点的坐标为( )
A.(2,﹣3) B.(﹣2,3) C.(﹣2,﹣3) D.(2,3)
4.若点在第二象限,则点在()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如果点与关于轴对称,则,的值分别为( )
A., B.,
C., D.,
6.如图是战机在空中展示的轴对称队形.以飞机B,C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(40,a),则飞机D的坐标为( )
A. B. C. D.
7.如果第二列第一行用有序数对(2,1)表示,那么数对(3,6)和(3,4)表示的位置是( )
A.同一行 B.同一列 C.同行同列 D.不同行不同列
8.如图,笑脸盖住的点的坐标可能为( )
A. B. C. D.
9.已知平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )
A.﹣3 B.﹣5 C.1或﹣3 D.1或﹣5
10.昌平公园建成于1990年,公园内有一个占地10000平方米的静明湖,另外建有弘文阁、碑亭、文节亭、诗田亭、逸步桥、牌楼等园林景观及古建筑.如图,分别以正东、正北方向为x轴、y轴建立平面直角坐标系,如果表示文节亭的点的坐标为(2,0),表示园中园的点的坐标为(-1,2),则表示弘文阁所在的点的坐标为( )
A.(-2,-3) B.(-2,-2)
C.(-3,-3) D.(-3,-4)
二、填空题
11.在平面直角坐标系中,点 P( 2,1)关于 x 轴的对称点的坐标为_____
12.点(3,0)关于y轴对称的点的坐标是_______
13.点P关于x轴对称点是,点P关于y轴对称点是,则__________.
14.点A(3m﹣1,2m)位于第一、三象限的角平分线上,则m=_____.
15.在平面直角坐标系中,点M(a,b)与点N(3,﹣1)关于x轴对称,则的值是_____.
16.如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为_____.
17.如图①,某广场地面是用..三种类型地砖平铺而成的,三种类型地砖上表面图案如图②所示,现用有序数对表示每一块地砖的位置:第一行的第一块(型)地砖记作,第二块(型)地时记作…若位置恰好为型地砖,则正整数,须满足的条是__________.
三、解答题
18.已知点P(2m+4,m-1).试分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,-3)点,且与x轴平行的直线上.
19.如图,在直角坐标系中,的三个顶点坐标分别为,,,请回答下列问题:
(1)作出关于轴的对称图形,并直接写出的顶点坐标;
(2)的面积为 .
20.如图,正方形网格中一线段的两个端点的坐标分别为
(1)在正方形网格中建立平面直角坐标系;
(2)若点在轴上运动,当长度最小时,点的坐标为 ,依据是
(3)在(2)的条件下,连接,求的面积.
21.已知:点,且点到轴、轴的距离相等.求点的坐标.
22.如图所示,三角形ABC三个顶点的坐标分别是A(2,-2),B(1,2),C(-2,-1).求三角形ABC的面积.
23.已知点,解答下列各题.
(1)点P在x轴上,求出点P的坐标.
(2)点Q的坐标为,直线轴;求出点P的坐标.
(3)若点P在第二象限,且它到x轴、y轴的距离相等,求的值.
参考答案:
1.D
【解析】
【分析】
四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
【详解】
解:∵点A的横坐标为正数、纵坐标为负数,
∴点A(5,-4)在第四象限,
故选D.
【点睛】
本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键.
2.B
【解析】
【分析】
根据各象限内点的坐标特征对各选项分析判断利用排除法求解.
【详解】
、,在轴上,故本选项不合题意;
、在第二象限,故本选项符合题意;
、在轴上,故本选项不合题意;
、在第四象限,故本选项不合题意.
答案:B.
【点睛】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
3.C
【解析】
【分析】
根据关于x轴对称点的坐标特点即可求解.
【详解】
解:∵关于x轴对称点的坐标特点:横坐标相同,纵坐标互为相反数,
∴点P(﹣2,3)关于x轴的对称点坐标是(﹣2,﹣3),
故答选:C.
【点睛】
此题主要考查关于x轴对称的点,解题的关键是熟知关于x轴对称点的坐标特点.
4.C
【解析】
【分析】
根据第二象限内的点的横坐标小于零,纵坐标大于零,可得关于a、b的不等式,再根据不等式的性质,可得B点的坐标符号.
【详解】
解:根据题意知,
解得:a<﹣1,b>2,
则a-3<0,1-b<0,
∴点在第三象限,
故选:C.
【点睛】
本题考查了点的坐标,利用第二象限内点的横坐标小于零,纵坐标大于零得出不等式,又利用不等式的性质得出B点的坐标符号是解题关键.
5.A
【解析】
【分析】
根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.即点P(x,y)关于y轴的对称点P′的坐标是(-x,y),进而得出答案.
【详解】
解:∵点P(-m,3)与点Q(-5,n)关于y轴对称,
∴m=-5,n=3,
故选:A.
【点睛】
此题主要考查了关于y轴对称点的性质,正确记忆关于坐标轴对称点的性质是解题关键.
6.B
【解析】
【分析】
直接利用关于y轴对称,纵坐标相同,横坐标互为相反数,进而得出答案.
【详解】
解:根据题意,点E与点D关于y轴对称,
∵飞机E的坐标为(40,a),
∴飞机D的坐标为(-40,a),
故选:B.
【点睛】
此题主要考查了关于y轴对称点的性质,正确记忆横纵坐标的符号关系是解题关键.
7.B
【解析】
【分析】
数对中第一个数字表示列数,第二个数字表示行数,据此可作出判断.
【详解】
解:第二列第一行用数对(2,1)表示,则数对(3,6)表示第三列,第六行,数对(3,4)表示表示第三列,第四行.所以数对(3,6)和(3,4)表示的位置是同一列不同行.
故选:B.
【点睛】
本题主要考查了坐标确定位置,一般用数对表示点位置的方法是第一个数字表示列,第二个数字表示行,也有例外,具体题要根据已知条件确定.
8.B
【解析】
【分析】
根据图形得出笑脸的位置,进而得出答案.
【详解】
解:由图形可得:笑脸盖住的点在第二象限,故笑脸盖住的点的坐标可能为( 6,3).
故选:B.
【点睛】
此题主要考查了点的坐标,得出笑脸的横纵坐标符号是解题关键.
9.A
【解析】
【分析】
根据点A(a+2,4)和B(3,2a+2)到x轴的距离相等,得到4=|2a+2|,即可解答.
【详解】
解:∵点A(a+2,4)和B(3,2a+2)到x轴的距离相等,
∴4=|2a+2|,a+2≠3,
解得:a= 3,
故选A.
【点睛】
考查点的坐标的相关知识;用到的知识点为:到x轴和y轴的距离相等的点的横纵坐标相等或互为相反数.
10.B
【解析】
【分析】
直接利用文节亭的点的坐标为(2,0),进而得出原点位置进而得出答案.
【详解】
如图所示:
弘文阁所在的点的坐标为:(-2,-2).
故选:B.
【点睛】
此题主要考查了坐标确定位置,正确得出原点位置是解题关键.
11.(2,1)
【解析】
【分析】
根据与x 轴对称的点的性质,求出对称点的坐标即可.
【详解】
∵对称点与点 P( 2,1)关于 x 轴对称
∴保持横坐标不变,纵坐标取相反数
∴对称点的坐标为
故答案为:.
【点睛】
本题考查了关于x 轴的对称点的坐标问题,掌握与x 轴对称的点的性质是解题的关键.
12.(-3,0)
【解析】
【分析】
根据平面直角坐标系中两个关于坐标轴成轴对称的点的坐标特点,直接用假设法设出相关点即可.
【详解】
解:点(m,n)关于y轴对称点的坐标(-m,n),
所以点(3,0)关于y轴对称的点的坐标为(-3,0).
故答案为:(-3,0).
【点睛】
本题考查平面直角坐标系点的对称性质:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
13.1
【解析】
【分析】
根据关于坐标轴的对称点的坐标特征,求出a,b的值,即可求解.
【详解】
∵点P关于x轴对称点是,
∴P(a,-2),
∵点P关于y轴对称点是,
∴b=-2,a=3,
∴1,
故答案是:1.
【点睛】
本题主要考查关于坐标轴对称的点的坐标特征,熟练掌握“关于x轴对称的两点,横坐标相等,纵坐标互为相反数;关于y轴对称的两点,横坐标互为相反数,纵坐标相等”是解题的关键.
14.1
【解析】
【分析】
根据第一、三象限角平分线上点的坐标特征得到得3m﹣1=2m,然后解关于m的一次方程即可.
【详解】
解:∵点A(3m﹣1,2m)在第一、三象限的角平分线上,
∴3m﹣1=2m,
解得:m=1.
故答案为:1
【点睛】
此题考查象限及点的坐标的有关性质,解题关键在于掌握其定义列出方程.
15.1
【解析】
【分析】
根据关于x轴对称的两点的横坐标相同,纵坐标互为相反数求得a、b的值即可求得答案.
【详解】
解:在直角坐标系中,关于x轴对称的两点,横坐标相同,纵坐标互为相反数,
∵点M(a,b)与点N(3,﹣1)关于x轴对称,
∴a=3,b=1,
∴=1,
故答案为:1.
【点睛】
本题考查了关于x轴对称的点的坐标特征,熟练掌握关于坐标轴对称的点的坐标特征是解题的关键.
16.(2,6)
【解析】
【分析】
此题涉及的知识点是平面直角坐标系图像性质的综合应用.过点M作MF⊥CD于F,过C作CE⊥OA于E,在Rt△CMF中,根据勾股定理即可求得MF与EM,进而就可求得OE,CE的长,从而求得C的坐标.
【详解】
∵四边形OCDB是平行四边形,点B的坐标为(16,0),
CD∥OA,CD=OB=16,
过点M作MF⊥CD于F,则
过C作CE⊥OA于E,
∵A(20,0),
∴OA=20,OM=10,
∴OE=OM ME=OM CF=10 8=2,
连接MC,
∴在Rt△CMF中,
∴点C的坐标为(2,6).
故答案为(2,6).
【点睛】
此题重点考察学生对坐标与图形性质的实际应用,勾股定理,注意数形结合思想在解题的关键.
17.m、n同为奇数或m、n同为偶数
【解析】
【分析】
几何图形,观察A型地砖的位置得到当列数为奇数时,行数也为奇数,当列数为偶数,行数也为偶数的,从而得到m、n满足的条件.
【详解】
解:观察图形,A型地砖在列数为奇数,行数也为奇数的位置上或列数为偶数,行数也为偶数的位置上,
若用(m,n)位置恰好为A型地砖,正整数m,n须满足的条件为m、n同为奇数或m、n同为偶数,
故答案为:m、n同为奇数或m、n同为偶数.
【点睛】
本题考查了坐标表示位置:通过类比点的坐标考查解决实际问题的能力和阅读理解能力.分析图形,寻找规律是关键.
18.(1)点P(-12,-9)(2)P(0,-3)
【解析】
【详解】
试题分析:(1)根据横纵坐标的大小关系得出m﹣1﹣(2m+4)=3,即可得出m的值,进而得出P点坐标;
(2)根据平行于x轴点的坐标性质得出m﹣1=﹣3,进而得出m的值,进而得出P点坐标.
解:(1)∵点P(2m+4,m﹣1),点P的纵坐标比横坐标大3,
∴m﹣1﹣(2m+4)=3,
解得:m=﹣8,
∴2m+4=﹣12,m﹣1=﹣9,
∴点P的坐标为:(﹣12,﹣9);
(2)∵点P在过A(2,﹣3)点,且与x轴平行的直线上,
∴m﹣1=﹣3,
解得:m=﹣2,
∴2m+4=0,
∴P点坐标为:(0,﹣3).
19.(1)图见解析,,,;(2).
【解析】
【分析】
(1)利用轴对称的性质即可画出,再根据坐标系中所画出的三角形即可写出其顶点坐标.
(2)如图利用割补法即可求出的面积.
【详解】
(1)如图,即为所求,由图可知,,.
.
(2)如图取E(1,-2),F(1,-5),G(4,-5),分别连接E、、G、F,由图可知四边形EGF为正方形.
所以,
即.
故答案为:.
【点睛】
本题考查利用轴对称作图,利用轴对称的性质找出对称点的位置是解决问题的关键.
20.(1)见解析;(2)(5,0),垂线段最短;(3)3
【解析】
【分析】
(1)根据点A和点B的坐标找到原点位置,并建立坐标系即可;
(2)根据垂线段最短的基本事实,过A作x轴的垂线,垂足为C,求出C坐标即可;
(3)以AC为底,计算△ABC的面积,利用公式计算结果即可.
【详解】
(1)如图所示:
(2),垂线段最短.
(3)如图所示:
所以的面积为.
【点睛】
考查平面直角坐标系内坐标以及几何的一些问题,学生要熟练掌握平面直角坐标系的相关知识点,并结合三角形等几何问题解出本题.
21.点的坐标或
【解析】
【分析】
根据到两坐标的距离相等,可得关于a的方程,根据解方程,可得答案.
【详解】
点到轴、轴的距离相等.
,
,
或,
点的坐标或.
【点睛】
本题考查了点的坐标,利用到两坐标的距离相等得出关于a的方程是解题关键.
22.三角形ABC的面积为7.5.
【解析】
【分析】
利用割补法即可求解.
【详解】
过点A,C分别作平行于y轴的直线,过点A,B分别作平行于x轴的直线,它们的交点为D,E,F,得到正方形ADEF,则该正方形的面积为4×4=16.
三角形ABD、三角形BCE、三角形ACF的面积分别是:,,.
所以三角形ABC的面积为16-2-4.5-2=7.5.
【点睛】
此题主要考查坐标与图形,解题的关键是熟知割补法的运用.
23.(1);(2);(3)2021
【解析】
【分析】
(1)根据x轴上点的坐标特征:纵坐标为0,列出方程即可求出结论;
(2)根据与y轴平行的直线上两点坐标关系:横坐标相等、纵坐标不相等即可求出结论;
(3)根据题意可得:点P的横纵坐标互为相反数,从而求出a的值,即可求出结论.
【详解】
解:(1)若点P在x轴上,
∴a+5=0
解得:a=-5
∴;
(2)∵点Q的坐标为,直线轴
∴
解得:a=3
∴;
(3)∵点P在第二象限,且它到x轴、y轴的距离相等
∴
解得:a=-1
∴==2021
【点睛】
此题考查的是根据题意,求点的坐标,掌握x轴上点的坐标特征、与y轴平行的直线上两点坐标关系和点到x轴、y轴的距离与坐标关系是解题关键.
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
