第四章几何图形初步【挑战满分】2022-2023学年数学七上阶段性复习精选精练(人教版 含解析)
文档属性
| 名称 | 第四章几何图形初步【挑战满分】2022-2023学年数学七上阶段性复习精选精练(人教版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 850.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-29 21:56:33 | ||
图片预览



文档简介
第四章几何图形初步
一、单选题
1.若一个棱柱有7个面,则它是( )
A.七棱柱 B.六棱柱 C.五棱柱 D.四棱柱
2.如图是正方体的一种展开图,那么在原正方体中与“我”字所在面相对的面上的汉字是( )
A.大 B.美 C.遂 D.宁
3.如图,BC=,D为AC的中点,DC=3cm,则AB的长是( )
A.cm B.4cm C.cm D.5cm
4.下列四个图中,是三棱锥的表面展开图的是( )
A. B. C. D.
5.如图所示,正方体的展开图为( )
A. B.
C. D.
6.①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
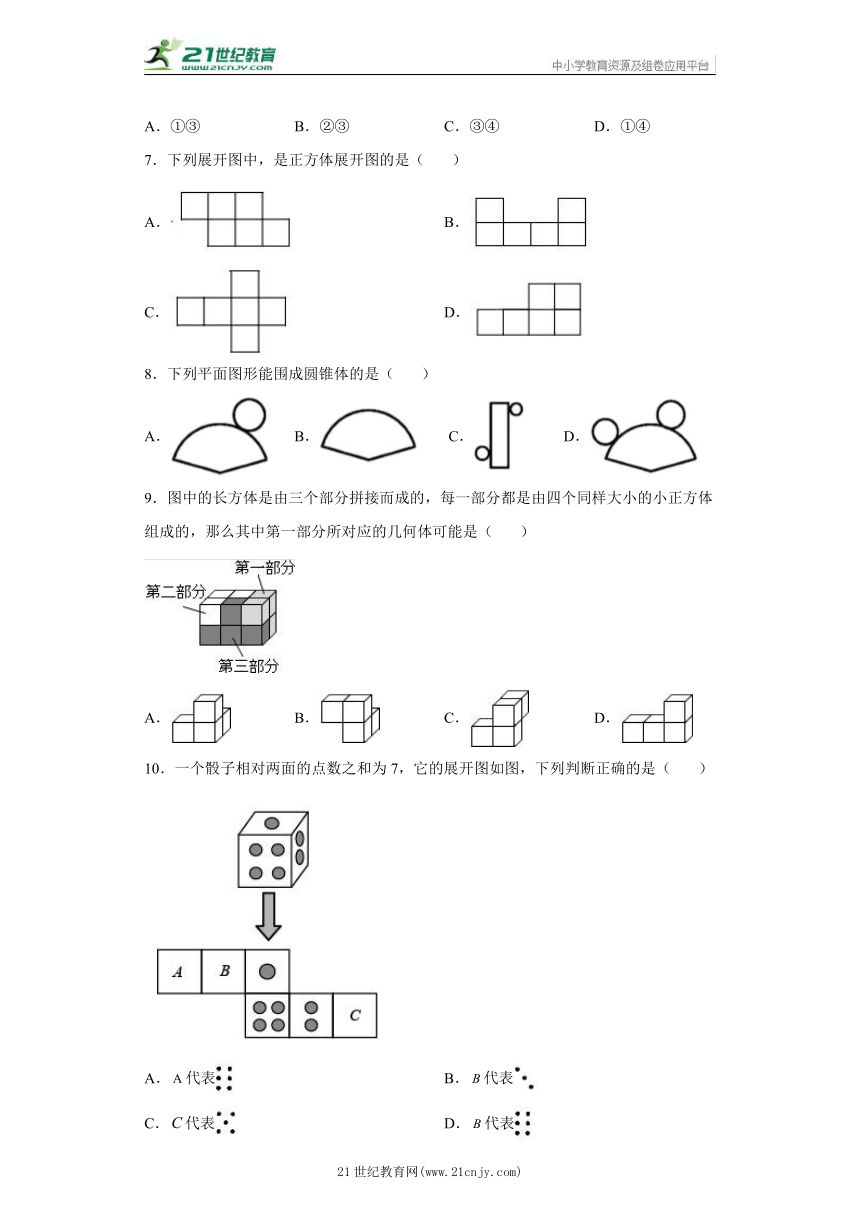
7.下列展开图中,是正方体展开图的是( )
A. B.
C. D.
8.下列平面图形能围成圆锥体的是( )
A. B. C. D.
9.图中的长方体是由三个部分拼接而成的,每一部分都是由四个同样大小的小正方体组成的,那么其中第一部分所对应的几何体可能是( )
A. B. C. D.
10.一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )
A.代表 B.代表
C.代表 D.代表
二、填空题
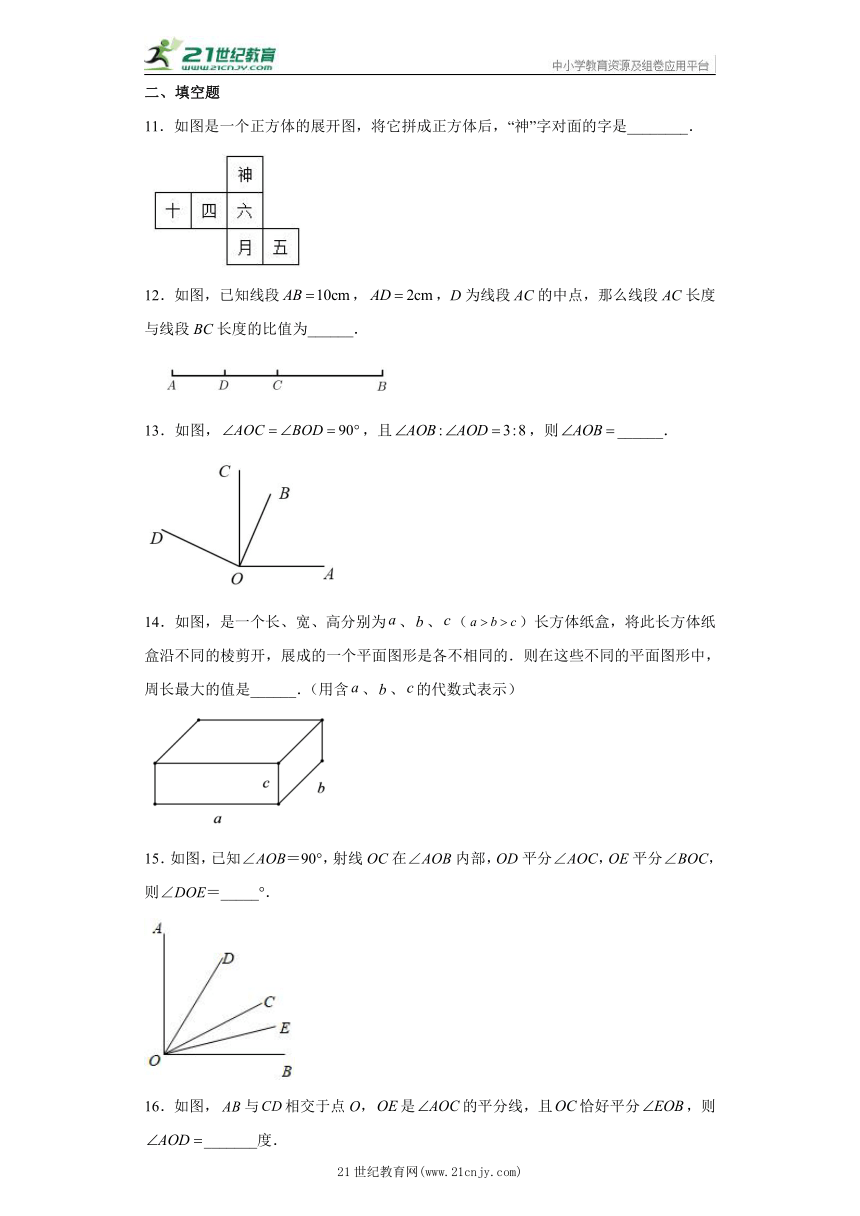
11.如图是一个正方体的展开图,将它拼成正方体后,“神”字对面的字是________.
12.如图,已知线段,,D为线段AC的中点,那么线段AC长度与线段BC长度的比值为______.
13.如图,,且,则______.
14.如图,是一个长、宽、高分别为、、()长方体纸盒,将此长方体纸盒沿不同的棱剪开,展成的一个平面图形是各不相同的.则在这些不同的平面图形中,周长最大的值是______.(用含、、的代数式表示)
15.如图,已知∠AOB=90°,射线OC在∠AOB内部,OD平分∠AOC,OE平分∠BOC,则∠DOE=_____°.
16.如图,与相交于点O,是的平分线,且恰好平分,则_______度.
17.将一根长4m的圆柱体木料锯成2段(2段都是圆柱体),表面积增加60dm2,这根木料的体积是______m3.
三、解答题
18.如图,点依次在直线上,,点也在直线上,且,若为的中点,求线段的长(用含的代数式表示).
19.如图1,将一段长为60厘米绳子AB拉直铺平后折叠(绳子无弹性,折叠处长度忽略不计),使绳子与自身一部分重叠.
(1)若将绳子AB沿M、N点折叠,点A、B分别落在处.
①如图2,若恰好重合于点O处,MN= cm,
②如图3,若点落在的左侧,且=20cm,求MN的长度;
③若=ncm,求MN的长度.(用含n的代数式表示)
(2)如图4,若将绳子AB沿N点折叠后,点B落在处,在重合部分N上沿绳子垂直方向剪断,将绳子分为三段,若这三段的长度由短到长的比为3:4:5,直接写出AN所有可能的长度.
20.如图,,为其内部一条射线.
(1)若平分,平分.求的度数;
(2)若,射线从起绕着点顺时针旋转,旋转的速度是每秒钟,设旋转的时间为,试求当时的值.
21.下面是一个多面体的表面展开图每个面上都标注了字母,(所有字母都写在这一多面体的外表面)请根据要求回答问题:
(1)如果面在前面,从左边看是,那么哪一面会在上面?
(2)如果从右面看是面面,面在后边那么哪一面会在上面?
(3)如果面在多面体的底部,从右边看是,那么哪一面会在前面.
参考答案:
1.C
【解析】
【分析】
根据棱柱有两个底面求出侧面数,即可选择.
【详解】
棱柱必有两个底面,则剩下7-2=5个面是侧面,所以为五棱柱.
故选C
【点睛】
本题考查认识立体图形棱柱,解题的关键是知道棱柱必有两个底面.
2.B
【解析】
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“我”与“美”是相对面.
故选:B.
【点睛】
本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手.
3.B
【解析】
【分析】
先根据已知等式得出AB与AC的等量关系,再根据线段的中点定义可得出AC的长,从而可得出答案.
【详解】
∵
∴,即
∵D为AC的中点,
∴
∴
故选:B.
【点睛】
本题考查了线段的和差倍分、线段的中点定义,掌握线段的中点定义是解题关键.
4.B
【解析】
【分析】
根据三棱锥是由四个三角形组成,即可求解
【详解】
解:A是四棱柱,故该选项不正确,不符合题意;
B是三棱锥,故该选项正确,符合题意;
C是四棱锥,故该选项不正确,不符合题意;
D是三棱柱,故该选项不正确,不符合题意;
故选B.
【点睛】
.本题考查了三棱锥的侧面展开图,解题的关键是掌握三棱锥是由四个三角形组成.
5.A
【解析】
【分析】
根据正方体的展开图的性质判断即可;
【详解】
A中展开图正确;
B中对号面和等号面是对面,与题意不符;
C中对号的方向不正确,故不正确;
D中三个符号的方位不相符,故不正确;
故答案选A.
【点睛】
本题主要考查了正方体的展开图考查,准确判断符号方向是解题的关键.
6.D
【解析】
【分析】
观察图形可知,①~④的小正方体的个数分别为4,3,3,2,其中②③组合不能 构成长方体,①④组合符合题意
【详解】
解:观察图形可知,①~④的小正方体的个数分别为4,3,3,2,其中②③组合不能构成长方体,①④组合符合题意
故选D
【点睛】
本题考查了立体图形,应用空间想象能力是解题的关键.
7.C
【解析】
【分析】
根据正方体的表面展开图共有11种情况,A,D是“田”型,对折不能折成正方体,B是“凹”型,不能围成正方体,由此可进行选择.
【详解】
解:根据正方体展开图特点可得C答案可以围成正方体,
故选:C.
【点睛】
此题考查了正方体的平面展开图.关键是掌握正方体展开图特点.
8.A
【解析】
【分析】
根据几何体的展开图的特征即可求解.
【详解】
A、是圆锥的展开图,故选项正确;
B、不是圆锥的展开图,故选项错误;
C、是长方体的展开图,故选项错误;
D、不是圆锥的展开图,故选项错误.
故选:A.
【点睛】
此题考查了展开图折叠成几何体,通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
9.B
【解析】
【分析】
观察长方体,可知第一部分所对应的几何体在长方体中,上面有二个正方体,下面有二个正方体,再在BC选项中根据图形作出判断.
【详解】
解:由长方体和第一部分所对应的几何体可知,
第一部分所对应的几何体上面有二个正方体,下面有二个正方体,并且与选项B相符.
故选:B.
【点睛】
本题考查了认识立体图形,找到长方体中,第一部分所对应的几何体的形状是解题的关键.
10.A
【解析】
【分析】
根据正方体展开图的对面,逐项判断即可.
【详解】
解:由正方体展开图可知,的对面点数是1;的对面点数是2;的对面点数是4;
∵骰子相对两面的点数之和为7,
∴代表,
故选:A.
【点睛】
本题考查了正方体展开图,解题关键是明确正方体展开图中相对面间隔一个正方形,判断哪两个面相对.
11.月
【解析】
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】
解:由正方体的展开图特点可得:“神”字对面的字是“月”.
故答案为:月.
【点睛】
此题考查了正方体相对两个面上的文字的知识;掌握常见类型展开图相对面上的两个字的特点是解决本题的关键.
12.
【解析】
【分析】
根据为线段的中点,可得,即可求解.
【详解】
D为AC的中点,
,
,
∵,
,
,
故答案为:.
【点睛】
本题主要考查了与线段中点有关的计算,求比值,解题的关键在于能够根据题意求出.
13.54°##54度
【解析】
【分析】
,通过,利用表示出,再根据角与角之间的关系,得到关于的方程,求解方程,即可得出答案.
【详解】
解:设,
,
,
,
,解得:,
故答案为:.
【点睛】
本题主要是考查了角的求解,熟练利用角与角之间的关系,求出未知角读书,这是解决本题的关键.
14.
【解析】
【分析】
只需要将最长的棱都剪开,最短的棱只剪一条即可得到周长最大的展开图形.
【详解】
如图,此平面图形就是长方形展开时周长最大的图形,的最大周长为,
故答案为.
【点睛】
此题主要考查了长方体的展开图的性质,根据展开图的性质得出最大周长的图形是解题关键.
15.45°.
【解析】
【分析】
根据角平分线的定义得到∠DOC=,∠COE=,根据角的和差即可得到结论.
【详解】
解:∵OD平分,
∴∠DOC=,
∵OE平分,
∴∠COE=,
∴∠DOE=∠DOC+∠COE==∠AOB=45°.
故答案为:45°.
【点睛】
本题考查了角平分线的定义以及有关角的计算,解题关键是熟练掌握角平分线的定义.
16.60
【解析】
【分析】
先根据角平分线的定义、平角的定义可得,再根据对顶角相等即可得.
【详解】
解:设,
是的平分线,
,
平分,
,
又,
,
解得,即,
由对顶角相等得:,
故答案为:60.
【点睛】
本题考查了角平分线的定义、平角的定义、对顶角相等,熟练掌握角平分线的定义是解题关键.
17.1.2
【解析】
【分析】
将一根长4m的圆柱体木料锯成2段,增加两个底面,又知表面积增加60dm2,由此求出这根木料的底面积,根据圆柱的体积公式即可计算.
【详解】
解:60dm2=0.6m2
0.6÷2=0.3(m2)
0.3×4=1.2(m3),
故这根木料的体积是1.2m3.
故答案为:1.2.
【点睛】
本题考查了计算圆柱的体积.解题的关键是掌握圆柱的体积公式.
18.a或a
【解析】
【分析】
分A、B在点D同侧,A、B在点D两侧,两种情况分别求解.
【详解】
解:当A、B在点D同侧时,
∵AC=CB=a,BD=AD,
∴AD=3BD=3a,
∵M是BD中点,
∴BM=DM=a,
∴CM=BC+BM=a;
当A、B在点D两侧时,
∵AC=CB=a,BD=AD,
∴AB=2a,AD=a,BD=a,
∵M为BD中点,
∴DM=BM=BD=a,
∴CM=AB-AC-BM=a.
【点睛】
本题考查了两点间的距离,中点的性质,解题的关键是灵活运用线段的和差,要分类讨论,以防遗漏.
19.(1)①30,②40cm,③cm或cm;(2)25 cm或27.5 cm或32.5 cm或35cm.
【解析】
【分析】
(1)①根据MN=MO+NO=AO+BO=AB即可求解;
②根据M、N分别为AA′、BB′的中点,得出AM=,BN=,再由MN= AB–(AM+ BN)即可求解;
③根据M、N分别为AA′、BB′的中点,得出AM=,BN=,然后分两种情况点A′落在点B′的左侧,点A′落在点B′的右侧,根据MN= AB–(AM+ BN)即可求解;
(2)根据三段的长度由短到长的比为3:4:5,得出绳子被剪分为15cm,20cm,25cm三段,然后分6中情况讨论,根据AN=AP+即可求解.
【详解】
解:(1)①MN=MO+NO=AO+BO=AB=30;
②因为AB=60 cm,A′B′=20 cm,
所以AA′+BB′=AB - A′B′=60 - 20=40 cm.
根据题意得,M、N分别为AA′、BB′的中点,
所以AM=,BN=.
AM+ BN=+==cm.
所以MN= AB–(AM+ BN)=60 - 20=40 cm.
③因为M、N分别为AA′、BB′的中点,所以AM=,BN=.
(ⅰ)如图,若点A′落在点B′的左侧,
AA′+BB′=AB - A′B′=(60– n) cm.
AM+ BN=+
==cm.
所以MN= AB–(AM+ BN)=cm.
(ⅱ)如图,若点A′落在点B′的右侧,
AA′+BB′=AB + A′B′=(60 +n)cm.
AM+ BN=+
==cm.
所以MN= AB–(AM+ BN)=(cm).
综上,MN的长度为cm或cm.
(2)如图,
∵三段的长度由短到长的比为3:4:5,
∴=15,=20,=25,
故绳子被剪分为15cm,20cm,25cm三段
当=15,=20,AP=25时,
AN=AP+=25+×20=35;
当=15,=25,AP=20时,
AN=AP+=20+×25=32.5;
当=20,=15,AP=25时,
AN=AP+=25+×15=32.5;
当=20,=25,AP=15时,
AN=AP+=15+×25=27.5;
当=25,=20,AP=15时,
AN=AP+=15+×20=25;
当=25,=15,AP=20时,
AN=AP+=20+×15=27.5.
综上AN所有可能的长度为:25 cm或27.5 cm或32.5 cm或35cm.
【点睛】
本题主要考查了线段的计算、线段的折叠问题、线段中点的性质,解题的关键是熟练掌握线段中点的性质,注意审题及分类讨论思想.
20.(1);(2)或,
【解析】
【分析】
(1)根据角平分线定义和角的和差计算即可;
(2)分四种情况讨论:①当OM在∠AOC内部时,②当OM在∠BOC内部时,③当OM在∠AOB外部,靠近射线OB时,④当OM在∠AOB外部,靠近射线OA时.分别列方程求解即可.
【详解】
(1)∵OE平分∠AOC,OF平分∠BOC,
∴∠1=∠AOC,∠2=∠BOC,
∴∠EOF=∠1+∠2=∠AOC+∠BOC=(∠AOC+∠BOC)=∠AOB.
∵∠AOB=160°,
∴∠EOF=80°.
(2)分四种情况讨论:
①当OM在∠AOC内部时,如图1.
∵∠AOC=100°,∠AOB=160°,
∴∠MOB=∠AOB-∠AOM=160°-.
∵∠AOM+∠MOC+∠MOB=∠AOC+∠MOB=200°,
∴100°+160°-=200°,
∴t=3.
②当OM在∠BOC内部时,如图2.
∵∠AOC=100°,∠AOB=160°,
∴∠BOC=∠AOB-∠AOC=160°-100°=60°.
∵∠AOM+∠MOC+∠MOB=∠AOM+∠COB=200°,
∴,
∴t=7.
③当OM在∠AOB外部,靠近射线OB时,如图3,
∵∠AOB=160°,∠AOC=100°,
∴∠BOC=160°-100°=60°.
∵∠AOM=,
∴∠MOB=∠AOM-∠AOB=,∠MOC=.
∵∠AOM+∠MOC+∠MOB=200°,
∴,解得:t=.
∵∠AOB=160°,
∴OM转到OB时,所用时间t=160°÷20°=8.
∵<8,
∴此时OM在∠BOC内部,不合题意,舍去.
④当OM在∠AOB外部,靠近射线OA时,如图4,
∵∠AOB=160°,∠AOC=100°,
∴∠BOC=160°-100°=60°.
∵,
∴∠MOC=∠AOM+∠AOC==,∠MOB=∠AOM+∠AOB==.
∵∠AOM+∠MOC+∠MOB=200°,
∴,解得:t=19.
当t=19时,=380°>360°,则OM转到了∠AOC的内部,不合题意,舍去.
综上所述:t=3s或t=7s.
【点睛】
本题考查了角的和差和一元一次方程的应用.用含t的式子表示出对应的角是解答本题的关键.
21.(1)面会在上面;(2)面会在上面;(3)面会在前面
【解析】
【分析】
利用长方体及其表面展开图的特点解题.这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
【详解】
解:(1)由图可知,如果F面在前面,B面在左面,那么“E”面下面,∵面“C”与面“E”相对,∴C面会在上面;
(2)由图可知,如果C面在右面,D面在后面,那么“F”面在下面,∵面“A”与面“F”相对,∴A面在上面.
(3)由图可知,如果面在多面体的底部,从右边看是,那么“E”面在后面,∵面“C”与面“E”相对,∴ 面会在前面
【点睛】
考查了几何体的展开图,注意正方体的空间图形,从相对面入手,分析及解答问题.
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
一、单选题
1.若一个棱柱有7个面,则它是( )
A.七棱柱 B.六棱柱 C.五棱柱 D.四棱柱
2.如图是正方体的一种展开图,那么在原正方体中与“我”字所在面相对的面上的汉字是( )
A.大 B.美 C.遂 D.宁
3.如图,BC=,D为AC的中点,DC=3cm,则AB的长是( )
A.cm B.4cm C.cm D.5cm
4.下列四个图中,是三棱锥的表面展开图的是( )
A. B. C. D.
5.如图所示,正方体的展开图为( )
A. B.
C. D.
6.①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
7.下列展开图中,是正方体展开图的是( )
A. B.
C. D.
8.下列平面图形能围成圆锥体的是( )
A. B. C. D.
9.图中的长方体是由三个部分拼接而成的,每一部分都是由四个同样大小的小正方体组成的,那么其中第一部分所对应的几何体可能是( )
A. B. C. D.
10.一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )
A.代表 B.代表
C.代表 D.代表
二、填空题
11.如图是一个正方体的展开图,将它拼成正方体后,“神”字对面的字是________.
12.如图,已知线段,,D为线段AC的中点,那么线段AC长度与线段BC长度的比值为______.
13.如图,,且,则______.
14.如图,是一个长、宽、高分别为、、()长方体纸盒,将此长方体纸盒沿不同的棱剪开,展成的一个平面图形是各不相同的.则在这些不同的平面图形中,周长最大的值是______.(用含、、的代数式表示)
15.如图,已知∠AOB=90°,射线OC在∠AOB内部,OD平分∠AOC,OE平分∠BOC,则∠DOE=_____°.
16.如图,与相交于点O,是的平分线,且恰好平分,则_______度.
17.将一根长4m的圆柱体木料锯成2段(2段都是圆柱体),表面积增加60dm2,这根木料的体积是______m3.
三、解答题
18.如图,点依次在直线上,,点也在直线上,且,若为的中点,求线段的长(用含的代数式表示).
19.如图1,将一段长为60厘米绳子AB拉直铺平后折叠(绳子无弹性,折叠处长度忽略不计),使绳子与自身一部分重叠.
(1)若将绳子AB沿M、N点折叠,点A、B分别落在处.
①如图2,若恰好重合于点O处,MN= cm,
②如图3,若点落在的左侧,且=20cm,求MN的长度;
③若=ncm,求MN的长度.(用含n的代数式表示)
(2)如图4,若将绳子AB沿N点折叠后,点B落在处,在重合部分N上沿绳子垂直方向剪断,将绳子分为三段,若这三段的长度由短到长的比为3:4:5,直接写出AN所有可能的长度.
20.如图,,为其内部一条射线.
(1)若平分,平分.求的度数;
(2)若,射线从起绕着点顺时针旋转,旋转的速度是每秒钟,设旋转的时间为,试求当时的值.
21.下面是一个多面体的表面展开图每个面上都标注了字母,(所有字母都写在这一多面体的外表面)请根据要求回答问题:
(1)如果面在前面,从左边看是,那么哪一面会在上面?
(2)如果从右面看是面面,面在后边那么哪一面会在上面?
(3)如果面在多面体的底部,从右边看是,那么哪一面会在前面.
参考答案:
1.C
【解析】
【分析】
根据棱柱有两个底面求出侧面数,即可选择.
【详解】
棱柱必有两个底面,则剩下7-2=5个面是侧面,所以为五棱柱.
故选C
【点睛】
本题考查认识立体图形棱柱,解题的关键是知道棱柱必有两个底面.
2.B
【解析】
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“我”与“美”是相对面.
故选:B.
【点睛】
本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手.
3.B
【解析】
【分析】
先根据已知等式得出AB与AC的等量关系,再根据线段的中点定义可得出AC的长,从而可得出答案.
【详解】
∵
∴,即
∵D为AC的中点,
∴
∴
故选:B.
【点睛】
本题考查了线段的和差倍分、线段的中点定义,掌握线段的中点定义是解题关键.
4.B
【解析】
【分析】
根据三棱锥是由四个三角形组成,即可求解
【详解】
解:A是四棱柱,故该选项不正确,不符合题意;
B是三棱锥,故该选项正确,符合题意;
C是四棱锥,故该选项不正确,不符合题意;
D是三棱柱,故该选项不正确,不符合题意;
故选B.
【点睛】
.本题考查了三棱锥的侧面展开图,解题的关键是掌握三棱锥是由四个三角形组成.
5.A
【解析】
【分析】
根据正方体的展开图的性质判断即可;
【详解】
A中展开图正确;
B中对号面和等号面是对面,与题意不符;
C中对号的方向不正确,故不正确;
D中三个符号的方位不相符,故不正确;
故答案选A.
【点睛】
本题主要考查了正方体的展开图考查,准确判断符号方向是解题的关键.
6.D
【解析】
【分析】
观察图形可知,①~④的小正方体的个数分别为4,3,3,2,其中②③组合不能 构成长方体,①④组合符合题意
【详解】
解:观察图形可知,①~④的小正方体的个数分别为4,3,3,2,其中②③组合不能构成长方体,①④组合符合题意
故选D
【点睛】
本题考查了立体图形,应用空间想象能力是解题的关键.
7.C
【解析】
【分析】
根据正方体的表面展开图共有11种情况,A,D是“田”型,对折不能折成正方体,B是“凹”型,不能围成正方体,由此可进行选择.
【详解】
解:根据正方体展开图特点可得C答案可以围成正方体,
故选:C.
【点睛】
此题考查了正方体的平面展开图.关键是掌握正方体展开图特点.
8.A
【解析】
【分析】
根据几何体的展开图的特征即可求解.
【详解】
A、是圆锥的展开图,故选项正确;
B、不是圆锥的展开图,故选项错误;
C、是长方体的展开图,故选项错误;
D、不是圆锥的展开图,故选项错误.
故选:A.
【点睛】
此题考查了展开图折叠成几何体,通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
9.B
【解析】
【分析】
观察长方体,可知第一部分所对应的几何体在长方体中,上面有二个正方体,下面有二个正方体,再在BC选项中根据图形作出判断.
【详解】
解:由长方体和第一部分所对应的几何体可知,
第一部分所对应的几何体上面有二个正方体,下面有二个正方体,并且与选项B相符.
故选:B.
【点睛】
本题考查了认识立体图形,找到长方体中,第一部分所对应的几何体的形状是解题的关键.
10.A
【解析】
【分析】
根据正方体展开图的对面,逐项判断即可.
【详解】
解:由正方体展开图可知,的对面点数是1;的对面点数是2;的对面点数是4;
∵骰子相对两面的点数之和为7,
∴代表,
故选:A.
【点睛】
本题考查了正方体展开图,解题关键是明确正方体展开图中相对面间隔一个正方形,判断哪两个面相对.
11.月
【解析】
【分析】
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】
解:由正方体的展开图特点可得:“神”字对面的字是“月”.
故答案为:月.
【点睛】
此题考查了正方体相对两个面上的文字的知识;掌握常见类型展开图相对面上的两个字的特点是解决本题的关键.
12.
【解析】
【分析】
根据为线段的中点,可得,即可求解.
【详解】
D为AC的中点,
,
,
∵,
,
,
故答案为:.
【点睛】
本题主要考查了与线段中点有关的计算,求比值,解题的关键在于能够根据题意求出.
13.54°##54度
【解析】
【分析】
,通过,利用表示出,再根据角与角之间的关系,得到关于的方程,求解方程,即可得出答案.
【详解】
解:设,
,
,
,
,解得:,
故答案为:.
【点睛】
本题主要是考查了角的求解,熟练利用角与角之间的关系,求出未知角读书,这是解决本题的关键.
14.
【解析】
【分析】
只需要将最长的棱都剪开,最短的棱只剪一条即可得到周长最大的展开图形.
【详解】
如图,此平面图形就是长方形展开时周长最大的图形,的最大周长为,
故答案为.
【点睛】
此题主要考查了长方体的展开图的性质,根据展开图的性质得出最大周长的图形是解题关键.
15.45°.
【解析】
【分析】
根据角平分线的定义得到∠DOC=,∠COE=,根据角的和差即可得到结论.
【详解】
解:∵OD平分,
∴∠DOC=,
∵OE平分,
∴∠COE=,
∴∠DOE=∠DOC+∠COE==∠AOB=45°.
故答案为:45°.
【点睛】
本题考查了角平分线的定义以及有关角的计算,解题关键是熟练掌握角平分线的定义.
16.60
【解析】
【分析】
先根据角平分线的定义、平角的定义可得,再根据对顶角相等即可得.
【详解】
解:设,
是的平分线,
,
平分,
,
又,
,
解得,即,
由对顶角相等得:,
故答案为:60.
【点睛】
本题考查了角平分线的定义、平角的定义、对顶角相等,熟练掌握角平分线的定义是解题关键.
17.1.2
【解析】
【分析】
将一根长4m的圆柱体木料锯成2段,增加两个底面,又知表面积增加60dm2,由此求出这根木料的底面积,根据圆柱的体积公式即可计算.
【详解】
解:60dm2=0.6m2
0.6÷2=0.3(m2)
0.3×4=1.2(m3),
故这根木料的体积是1.2m3.
故答案为:1.2.
【点睛】
本题考查了计算圆柱的体积.解题的关键是掌握圆柱的体积公式.
18.a或a
【解析】
【分析】
分A、B在点D同侧,A、B在点D两侧,两种情况分别求解.
【详解】
解:当A、B在点D同侧时,
∵AC=CB=a,BD=AD,
∴AD=3BD=3a,
∵M是BD中点,
∴BM=DM=a,
∴CM=BC+BM=a;
当A、B在点D两侧时,
∵AC=CB=a,BD=AD,
∴AB=2a,AD=a,BD=a,
∵M为BD中点,
∴DM=BM=BD=a,
∴CM=AB-AC-BM=a.
【点睛】
本题考查了两点间的距离,中点的性质,解题的关键是灵活运用线段的和差,要分类讨论,以防遗漏.
19.(1)①30,②40cm,③cm或cm;(2)25 cm或27.5 cm或32.5 cm或35cm.
【解析】
【分析】
(1)①根据MN=MO+NO=AO+BO=AB即可求解;
②根据M、N分别为AA′、BB′的中点,得出AM=,BN=,再由MN= AB–(AM+ BN)即可求解;
③根据M、N分别为AA′、BB′的中点,得出AM=,BN=,然后分两种情况点A′落在点B′的左侧,点A′落在点B′的右侧,根据MN= AB–(AM+ BN)即可求解;
(2)根据三段的长度由短到长的比为3:4:5,得出绳子被剪分为15cm,20cm,25cm三段,然后分6中情况讨论,根据AN=AP+即可求解.
【详解】
解:(1)①MN=MO+NO=AO+BO=AB=30;
②因为AB=60 cm,A′B′=20 cm,
所以AA′+BB′=AB - A′B′=60 - 20=40 cm.
根据题意得,M、N分别为AA′、BB′的中点,
所以AM=,BN=.
AM+ BN=+==cm.
所以MN= AB–(AM+ BN)=60 - 20=40 cm.
③因为M、N分别为AA′、BB′的中点,所以AM=,BN=.
(ⅰ)如图,若点A′落在点B′的左侧,
AA′+BB′=AB - A′B′=(60– n) cm.
AM+ BN=+
==cm.
所以MN= AB–(AM+ BN)=cm.
(ⅱ)如图,若点A′落在点B′的右侧,
AA′+BB′=AB + A′B′=(60 +n)cm.
AM+ BN=+
==cm.
所以MN= AB–(AM+ BN)=(cm).
综上,MN的长度为cm或cm.
(2)如图,
∵三段的长度由短到长的比为3:4:5,
∴=15,=20,=25,
故绳子被剪分为15cm,20cm,25cm三段
当=15,=20,AP=25时,
AN=AP+=25+×20=35;
当=15,=25,AP=20时,
AN=AP+=20+×25=32.5;
当=20,=15,AP=25时,
AN=AP+=25+×15=32.5;
当=20,=25,AP=15时,
AN=AP+=15+×25=27.5;
当=25,=20,AP=15时,
AN=AP+=15+×20=25;
当=25,=15,AP=20时,
AN=AP+=20+×15=27.5.
综上AN所有可能的长度为:25 cm或27.5 cm或32.5 cm或35cm.
【点睛】
本题主要考查了线段的计算、线段的折叠问题、线段中点的性质,解题的关键是熟练掌握线段中点的性质,注意审题及分类讨论思想.
20.(1);(2)或,
【解析】
【分析】
(1)根据角平分线定义和角的和差计算即可;
(2)分四种情况讨论:①当OM在∠AOC内部时,②当OM在∠BOC内部时,③当OM在∠AOB外部,靠近射线OB时,④当OM在∠AOB外部,靠近射线OA时.分别列方程求解即可.
【详解】
(1)∵OE平分∠AOC,OF平分∠BOC,
∴∠1=∠AOC,∠2=∠BOC,
∴∠EOF=∠1+∠2=∠AOC+∠BOC=(∠AOC+∠BOC)=∠AOB.
∵∠AOB=160°,
∴∠EOF=80°.
(2)分四种情况讨论:
①当OM在∠AOC内部时,如图1.
∵∠AOC=100°,∠AOB=160°,
∴∠MOB=∠AOB-∠AOM=160°-.
∵∠AOM+∠MOC+∠MOB=∠AOC+∠MOB=200°,
∴100°+160°-=200°,
∴t=3.
②当OM在∠BOC内部时,如图2.
∵∠AOC=100°,∠AOB=160°,
∴∠BOC=∠AOB-∠AOC=160°-100°=60°.
∵∠AOM+∠MOC+∠MOB=∠AOM+∠COB=200°,
∴,
∴t=7.
③当OM在∠AOB外部,靠近射线OB时,如图3,
∵∠AOB=160°,∠AOC=100°,
∴∠BOC=160°-100°=60°.
∵∠AOM=,
∴∠MOB=∠AOM-∠AOB=,∠MOC=.
∵∠AOM+∠MOC+∠MOB=200°,
∴,解得:t=.
∵∠AOB=160°,
∴OM转到OB时,所用时间t=160°÷20°=8.
∵<8,
∴此时OM在∠BOC内部,不合题意,舍去.
④当OM在∠AOB外部,靠近射线OA时,如图4,
∵∠AOB=160°,∠AOC=100°,
∴∠BOC=160°-100°=60°.
∵,
∴∠MOC=∠AOM+∠AOC==,∠MOB=∠AOM+∠AOB==.
∵∠AOM+∠MOC+∠MOB=200°,
∴,解得:t=19.
当t=19时,=380°>360°,则OM转到了∠AOC的内部,不合题意,舍去.
综上所述:t=3s或t=7s.
【点睛】
本题考查了角的和差和一元一次方程的应用.用含t的式子表示出对应的角是解答本题的关键.
21.(1)面会在上面;(2)面会在上面;(3)面会在前面
【解析】
【分析】
利用长方体及其表面展开图的特点解题.这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
【详解】
解:(1)由图可知,如果F面在前面,B面在左面,那么“E”面下面,∵面“C”与面“E”相对,∴C面会在上面;
(2)由图可知,如果C面在右面,D面在后面,那么“F”面在下面,∵面“A”与面“F”相对,∴A面在上面.
(3)由图可知,如果面在多面体的底部,从右边看是,那么“E”面在后面,∵面“C”与面“E”相对,∴ 面会在前面
【点睛】
考查了几何体的展开图,注意正方体的空间图形,从相对面入手,分析及解答问题.
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
