展开和折叠(第一课时)

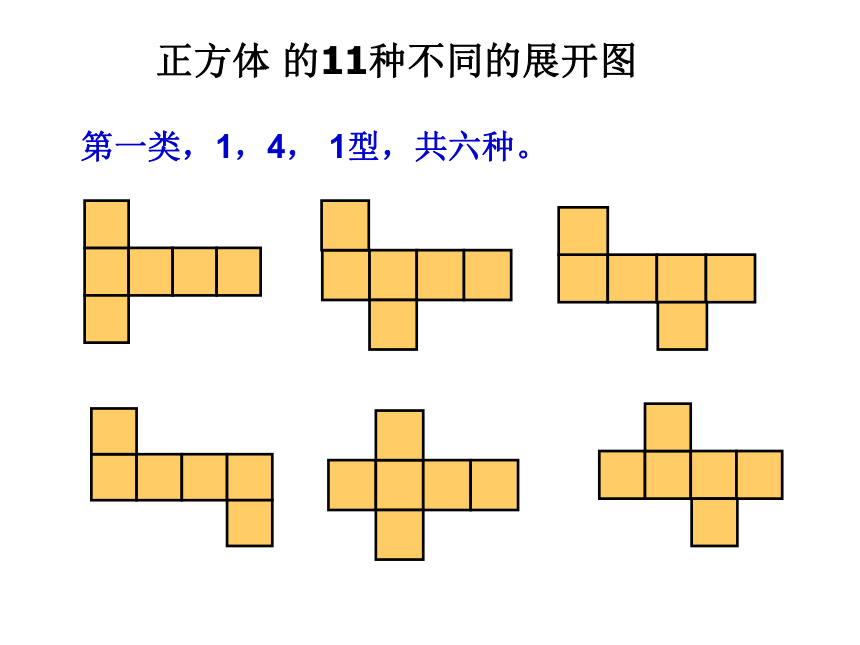
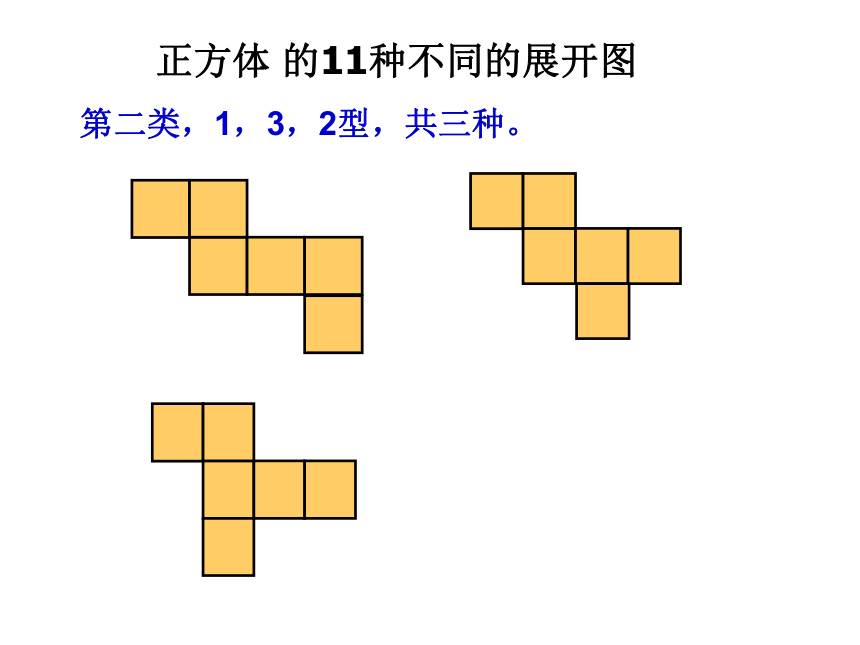
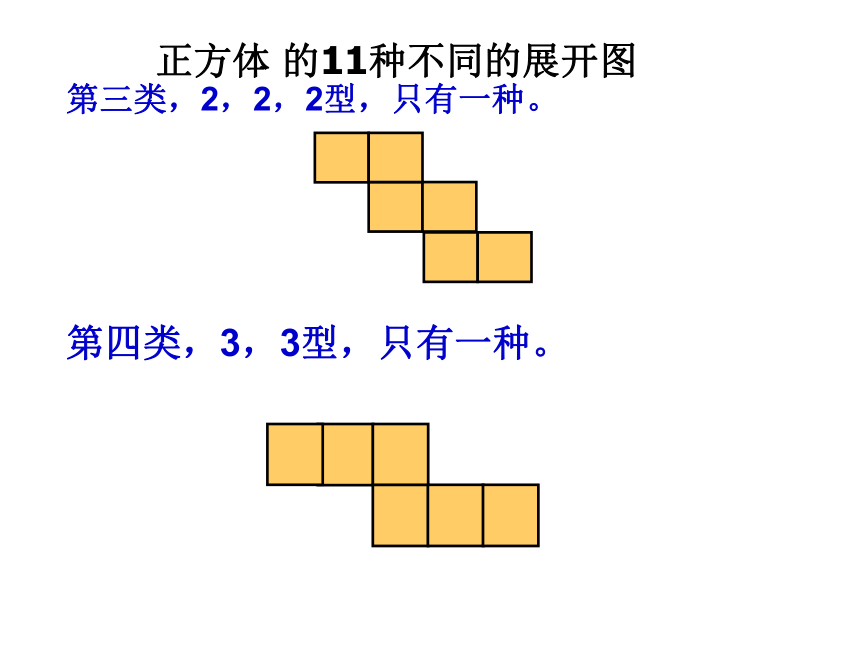
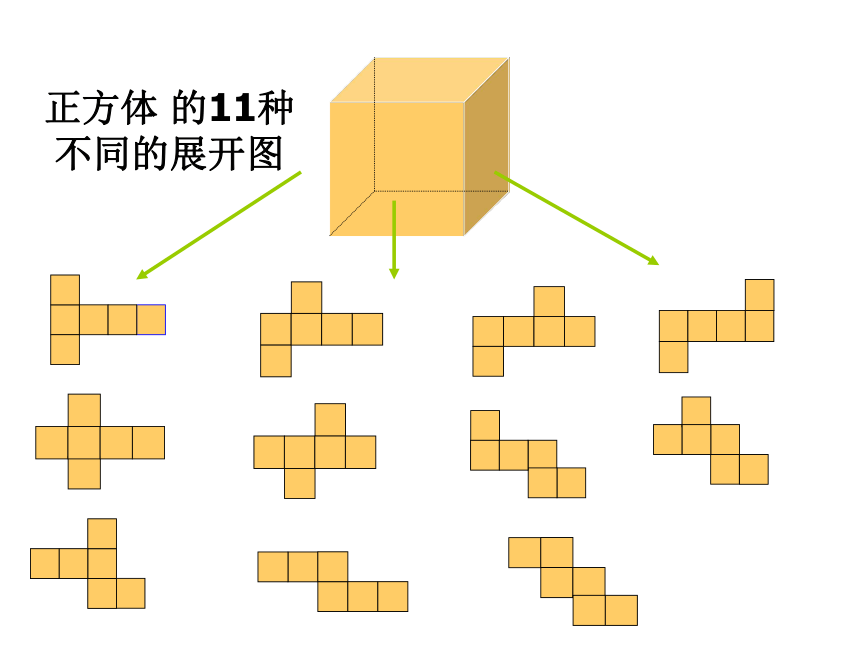
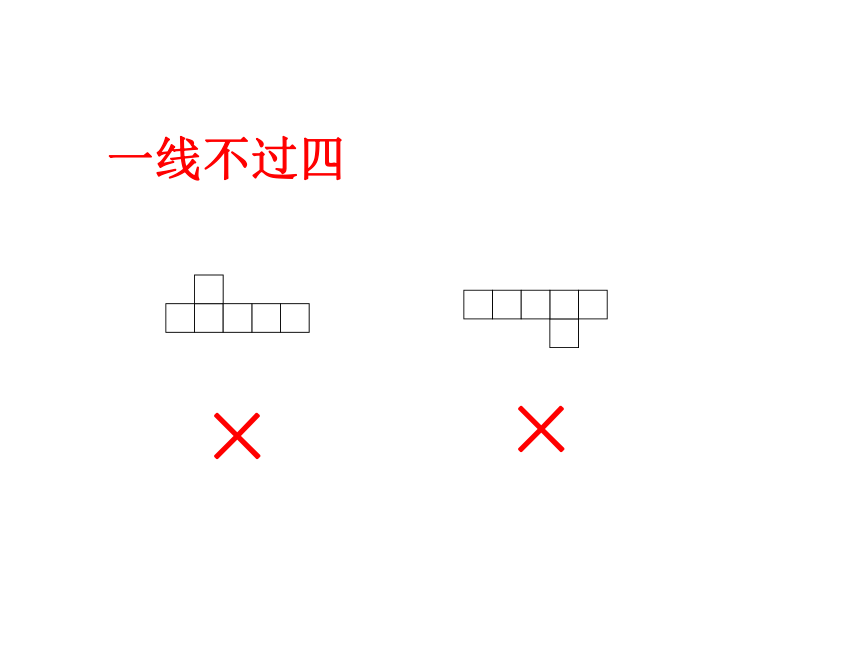
课件38张PPT。展开和折叠第一类，1，4， 1型，共六种。正方体 的11种不同的展开图 第二类，1，3，2型，共三种。正方体 的11种不同的展开图 第三类，2，2，2型，只有一种。第四类，3，3型，只有一种。正方体 的11种不同的展开图 正方体 的11种不同的展开图 正方体的表面展开图用“口诀”：一线不过四，
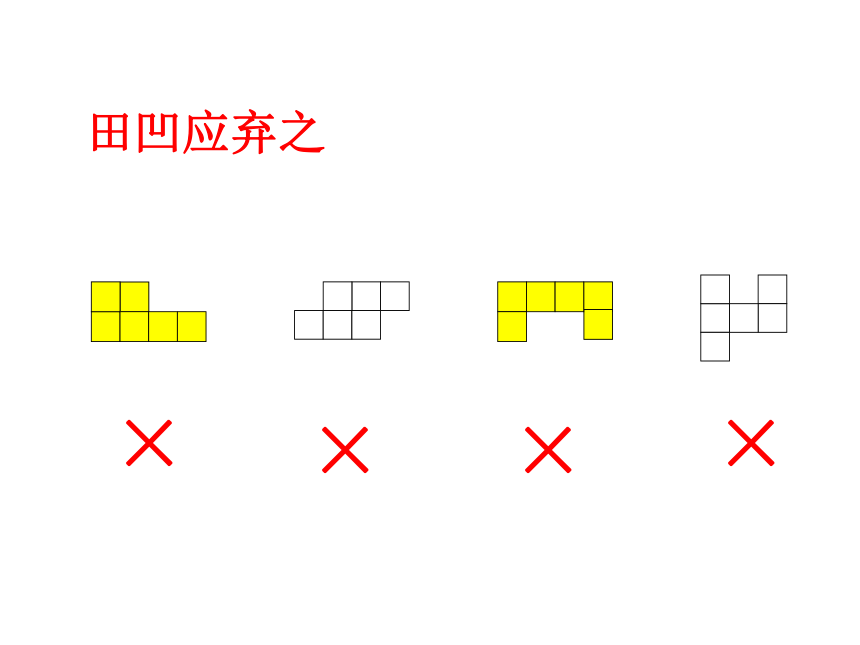
田凹应弃之;
相间、“Z”端是对面，
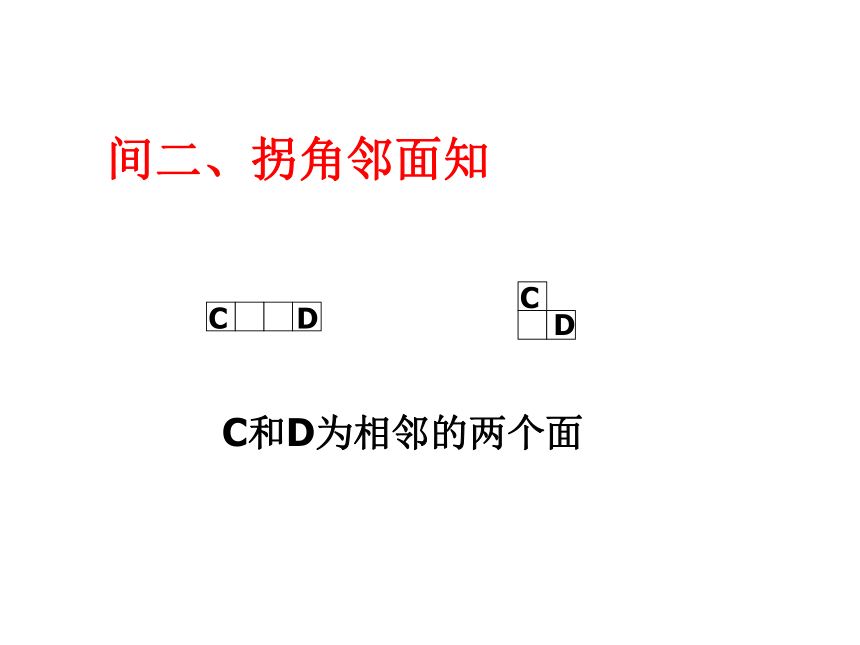
间二、拐角邻面知。总结规律：一线不过四××田凹应弃之××××相间、“Z”端是对面ABABA和B为相对的两个面间二、拐角邻面知CCDDC和D为相邻的两个面想一想
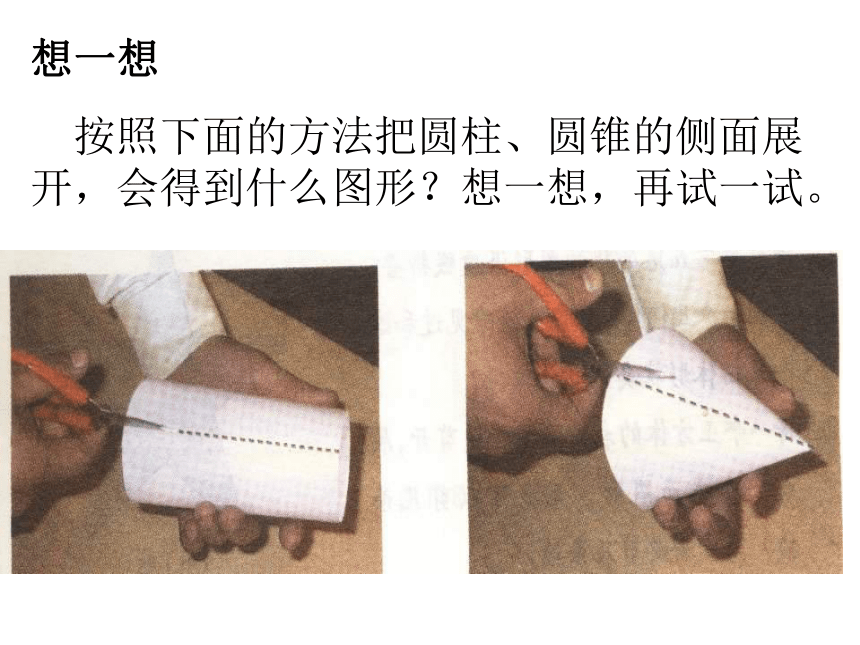
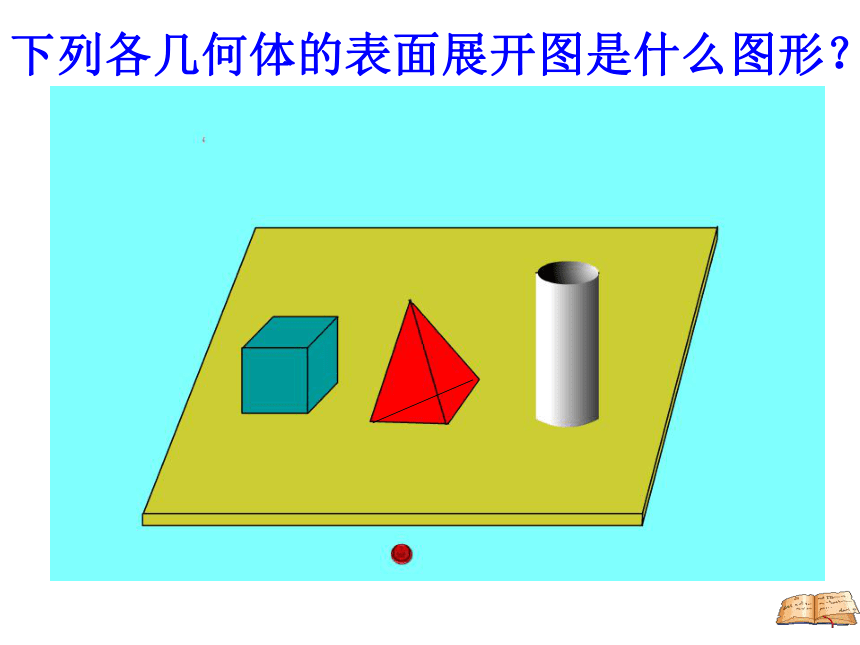
按照下面的方法把圆柱、圆锥的侧面展开，会得到什么图形？想一想，再试一试。下列各几何体的表面展开图是什么图形？画一画：三棱柱的表面展开图是什么？三棱柱的表面展开图是两个完全相同的三角形(作底面)和
三个长方形(作侧面)想一想：四棱柱的表面展开图是什么？做一做图1-2中左边的图形经过折叠能围成右边的棱柱吗?讨论:什么时候左边的图不能围成右 边的图?总结：n棱柱的表面展开图是什么？棱柱的平面展开图必须具备两个条件
1.中间的长方形个数与两侧多边形的边数相同
2.两个多边形，应位于中间长方形两侧想一想：三棱锥的展开图是什么图形？三棱锥的展开图是：想一想：四棱锥的展开图是什么图形？四棱锥的展开图是：n棱锥的表面展开图是什么？议一议想一想：
下列的图形都是正方体的展开图吗？(5)(2)(6)(3)(1)(4)(√)(√)(√)(×)(×)(√) 1、如图，第一行的几何体表面展开后得到的第二行的某个平面图形，请用线连一连。2、下面图形经过折叠能否围成棱柱？(3)可以折成棱柱 (1)侧面数(4个)≠底面边数(3条)，不能围成棱柱．(2)两底面在侧面展开图的同一端,不在两端,所以也不能
围成棱柱．4．下图所示的平面图形中不能围成三棱柱的是( )B5.下列哪个平面图形沿虚线折叠不能围成正方体的是( )B6、右图需再添上一个面，折叠后才能围成一个正方体，下面是四位同学补画的情况（图中阴影部分），其中正确的是（ ） A． Ｂ．　　　　Ｃ．　　　　　Ｄ．
B中考链接
1、李明为好友制作一个正方体礼品盒，六面上
各有一字，连起来就是“预祝中考成功”，其中“预”
的对面是“中”，“成”的对面是“功”，则它的平面展
开图可能是（　） Ａ．Ｂ．Ｃ．Ｄ．C2、在下面的图形中，不是正方体表面展开图
的是（ ）
A． B． C． D．c图1图23、如图1，是一个小正方体的侧面展开图，小正方体从如图2所示的位置依次翻到第1格、第2格、第3格，这时小正方体朝上面的字是（ ）
A．和 B．谐 C．社 D．会
D5、如图，将一块正方形纸片沿对角线折叠一次，
然后在得到的三角形的三个角上各挖去一个圆洞，
最后将正方形纸片展开，得到的图案是（　　）
c8、如图是一个食品包装盒的侧面展开图。
（1）请写出这个包装盒的多面体形状的名称；
（2）请根据图中所标的尺寸，计算这个多面体
的侧面积和全面积（侧面积与两个底面体之和）。（Ⅲ）先猜想再实践，发展几何直觉 如图是一个正方体纸盒的展开图，想一想，再试一试面A，面B，面C的对面各是哪个面？ ABCDEF