第23章 旋转【挑战满分】2022-2023学年数学九上阶段性复习精选精练(人教版 含解析)
文档属性
| 名称 | 第23章 旋转【挑战满分】2022-2023学年数学九上阶段性复习精选精练(人教版 含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-29 00:00:00 | ||
图片预览




文档简介
第23章 旋转
一、单选题
1.已知点与点关于原点对称,则点的坐标( )
A. B. C. D.
2.把四张扑克牌所摆放的顺序与位置如下,小杨同学选取其中一张扑克牌把他颠倒后在放回原来的位置,那么扑克牌的摆放顺序与位置都没变化,那么小杨同学所选的扑克牌是( )
A. B. C. D.
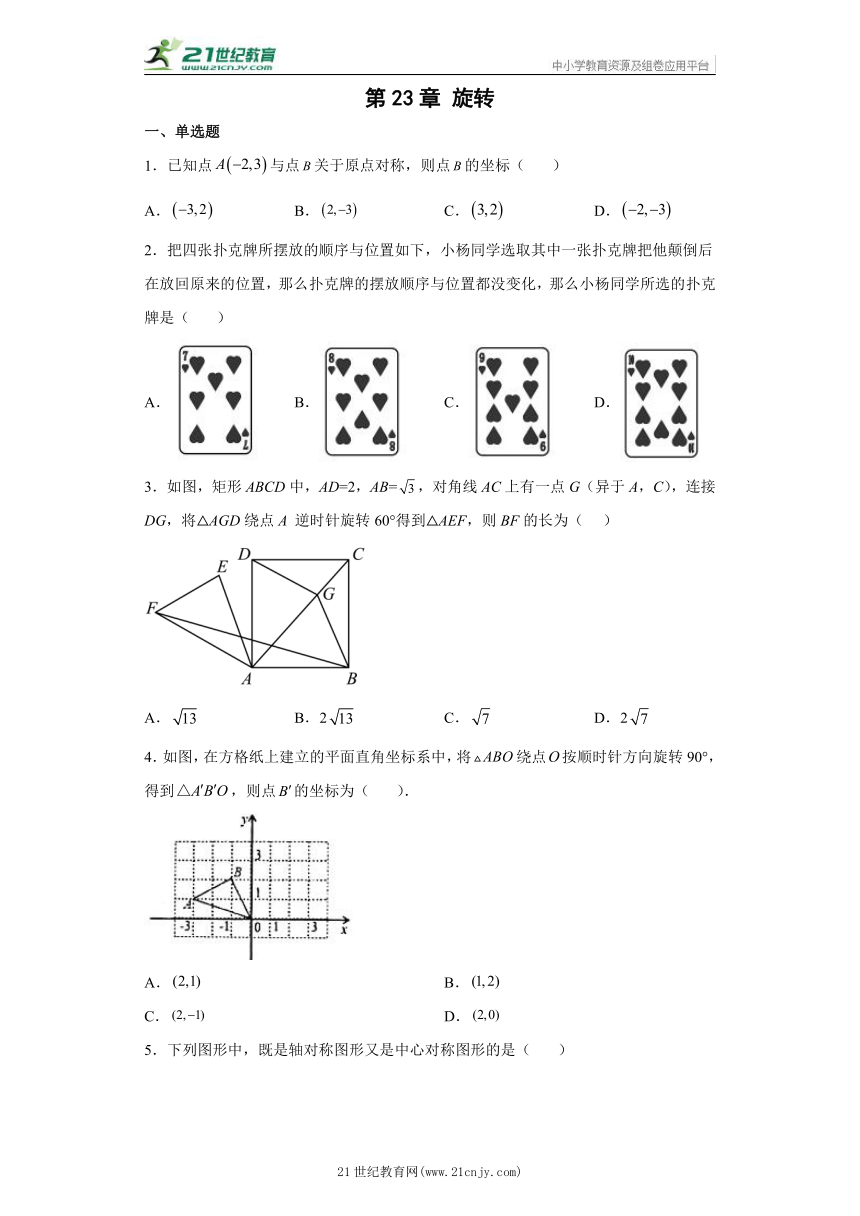
3.如图,矩形ABCD中,AD=2,AB=,对角线AC上有一点G(异于A,C),连接 DG,将△AGD绕点A 逆时针旋转60°得到△AEF,则BF的长为( )
A. B.2 C. D.2
4.如图,在方格纸上建立的平面直角坐标系中,将绕点按顺时针方向旋转90°,得到,则点的坐标为( ).
A. B.
C. D.
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
6.如图,在中,,,,将绕点顺时针旋转度得到,当点的对应点恰好落在边上时,则的长为( )
A.1.6 B.1.8 C.2 D.2.6
7.若P(x,3)与点Q(4,y)关于原点对称,则xy的值是( )
A.12 B.﹣12 C.64 D.﹣64
8.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
9.如图,将绕点逆时针旋转得到,若且于点,则的度数为( )
A. B. C. D.
10.点 A(x,y)在第二象限内,且│x│=2,│y│=3,则点A关于原点对称的点的坐标为( )
A.(-2,3) B.(2,-3) C.(-3,2) D.(3,-2)
二、填空题
11.下列4种图案中,是中心对称图形的有_____个.
12.已知点与点关于原点对称,则的值为_________.
13.问题背景:如图,将绕点逆时针旋转60°得到,与交于点,可推出结论:
问题解决:如图,在中,,,.点是内一点,则点到三个顶点的距离和的最小值是___________
14.如图,将绕点A逆时针旋转角得到,点B的对应点D恰好落在边上,若,则旋转角的度数是______.
15.在平面直角坐标系中,直线分别交x轴、y轴于C、A两点.将射线绕着点A顺时针旋转,得到射线.点D为上的动点,点B为上的动点,点C在的内部.
(1)周长的最小值是____________________;
(2)当的周长取得最小值,且时,的面积为__________.
16.如图,在Rt△ABC中,∠ACB=90°,,点D为AB的中点,点P在AC上,且CP=1,将CP绕点C在平面内旋转,点P的对应点为点Q,连接AQ,DQ.当∠ADQ=90°时,AQ的长为______.
17.如图,在正方形网格中,格点绕某点顺时针旋转角得到格点,点与点,点与点,点与点是对应点,则_____度.
三、解答题
18.如图,等腰三角形中,,.作于点,将线段绕着点顺时针旋转角后得到线段,连接.
(1)求证:;
(2)延长线段,交线段于点.求的度数(用含有的式子表示) .
19.问题情境:
数学活动课上,老师让同学们以“三角形的旋转”为主题开展数学活动,△ABC和△DEC是两个全等的直角三角形纸片,其中∠ACB=∠DCE=90°,∠B=∠E=30°,AB=DE=4.
解决问题:
(1)如图1,智慧小组将△DEC绕点C顺时针旋转,发现当点D恰好落在AB边上时,DE∥AC,请你帮他们证明这个结论;
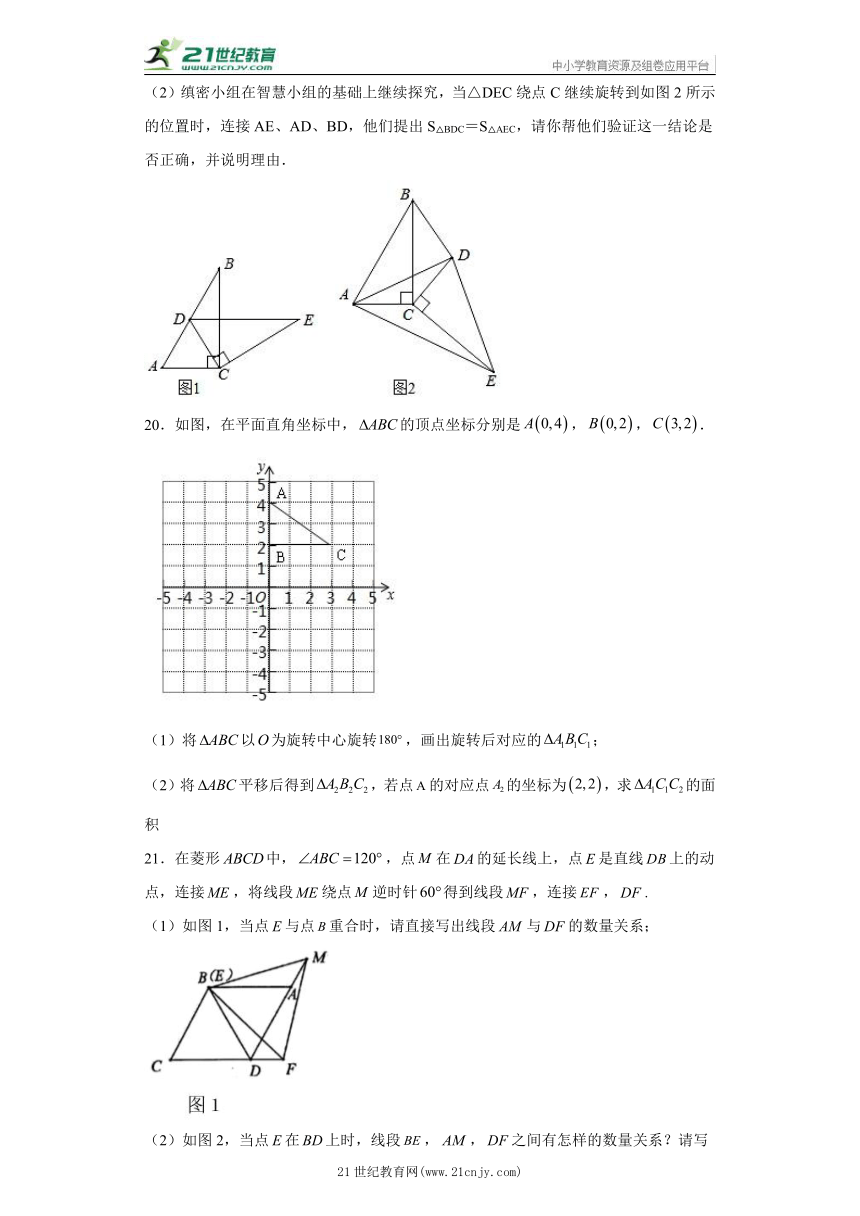
(2)缜密小组在智慧小组的基础上继续探究,当△DEC绕点C继续旋转到如图2所示的位置时,连接AE、AD、BD,他们提出S△BDC=S△AEC,请你帮他们验证这一结论是否正确,并说明理由.
20.如图,在平面直角坐标中,的顶点坐标分别是,,.
(1)将以为旋转中心旋转,画出旋转后对应的;
(2)将平移后得到,若点的对应点的坐标为,求的面积
21.在菱形中,,点在的延长线上,点是直线上的动点,连接,将线段绕点逆时针得到线段,连接,.
(1)如图1,当点与点重合时,请直接写出线段与的数量关系;
(2)如图2,当点在上时,线段,,之间有怎样的数量关系?请写出结论并给出证明;
(3)当点在直线上时,若,,,请直接写出线段的长.
参考答案:
1.B
【解析】
【分析】
根据关于原点对称点的坐标变化特征直接判断即可.
【详解】
解:点与点关于原点对称,则点的坐标为,
故选:B.
【点睛】
本题考查了关于原点对称点的坐标,解题关键是明确关于原点对称的两个点横纵坐标都互为相反数.
2.D
【解析】
【分析】
根据题意,图形是中心对称图形即可得出答案.
【详解】
由题意可知,图形是中心对称图形,可得答案为D,
故选:D.
【点睛】
本题考查了图形的中心对称的性质,掌握中心图形的性质是解题的关键.
3.A
【解析】
【分析】
过点F作FH⊥BA交BA的延长线于点H,则∠FHA=90°,△AGD绕点A 逆时针旋转60°得到△AEF,得∠FAD=60°,AF=AD=2,又由四边形ABCD是矩形,∠BAD=90°,得到∠FAH=30°,在Rt△AFH中,FH=AF=1,由勾股定理得AH= ,得到BH=AH+AB=2 ,再由勾股定理得BF=.
【详解】
解:如图,过点F作FH⊥BA交BA的延长线于点H,则∠FHA=90°,
∵△AGD绕点A 逆时针旋转60°得到△AEF
∴∠FAD=60°,AF=AD=2,
∵ 四边形ABCD是矩形
∴ ∠BAD=90°
∴∠BAF=∠FAD+ ∠BAD=150°
∴∠FAH=180°-∠BAF=30°
在Rt△AFH中,FH=AF=1
由勾股定理得
AH=
在Rt△BFH中,FH=1,BH=AH+AB=2
由勾股定理得
BF=
故BF的长.
故选:A
【点睛】
本题考查了图形的旋转,矩形的性质,含30度角的直角三角形的性质,勾股定理等知识,解决此题的关键在于作出正确的辅助线.
4.A
【解析】
【分析】
根据网格结构作出旋转后的图形,然后根据平面直角坐标系写出点B′的坐标即可.
【详解】
△A′B′O如图所示,点B′(2,1).
故选A.
【点睛】
本题考查了坐标与图形变化,熟练掌握网格结构,作出图形是解题的关键.
5.B
【解析】
【分析】
利用轴对称图形和中心对称图形的定义逐项判断即可.
【详解】
A.是轴对称图形不是中心对称图形.故A不符合题意.
B.是轴对称图形也是中心对称图形.故B符合题意.
C.是轴对称图形但不是中心对称图形.故C不符合题意.
D.不是中心对称图形也不是轴对称图形.故D不符合题意.
故选:B
【点睛】
本题考查轴对称图形和中心对称图形的定义,根据选项灵活判断其图形是否符合题意是解本题的关键.
6.A
【解析】
【分析】
由将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上,可得AD=AB,又由∠B=60°,可证得△ABD是等边三角形,继而可得BD=AB=2,则可求得答案.
【详解】
由旋转的性质可知,,
∵,,
∴为等边三角形,
∴,
∴,
故选A.
【点睛】
此题考查旋转的性质,解题关键在于利用旋转的性质得出AD=AB
7.A
【解析】
【分析】
直接利用关于原点对称点的性质得出x,y的值,进而得出答案.
【详解】
∵与点关于原点对称,
∴,,
∴.
故选A.
【点睛】
此题主要考查了关于原点对称点的性质,正确记忆横纵坐标的符号是解题关键.
8.C
【解析】
【分析】
根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.
【详解】
解:A.是轴对称图形,不是中心对称图形,故本选项不符合题意;
B.既不是轴对称图形,又不是中心对称图形,故本选项不符合题意;
C.既是轴对称图形,又是中心对称图形,故本选项符合题意;
D.不是轴对称图形,是中心对称图形,故本选项不符合题意.
故选:C.
【点睛】
本题考查了中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
9.C
【解析】
【分析】
由旋转的性质可得∠BAD=55°,∠E=∠ACB=70°,由直角三角形的性质可得∠DAC=20°,即可求解.
【详解】
解:∵将△ABC绕点A逆时针旋转55°得△ADE,
∴∠BAD=55°,∠E=∠ACB=70°,
∵AD⊥BC,
∴∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=75°.
故选C.
【点睛】
本题考查了旋转的性质,掌握旋转的性质是本题的关键.
10.B
【解析】
【分析】
根据A(x,y)在第二象限内可以判断x,y的符号,再根据|x|=2,|y|=3就可以确定点A的坐标,进而确定点A关于原点的对称点的坐标.
【详解】
∵A(x,y)在第二象限内,
∴x<0 y>0,
又∵|x|=2,|y|=3,
∴x=-2, y=3,
∴点A关于原点的对称点的坐标是(2,-3).
故选:B.
【点睛】
本题考查了关于原点对称的点的坐标,由点所在的象限能判断出坐标的符号,同时考查了关于原点对称的点坐标之间的关系,难度一般.
11.2
【解析】
【分析】
根据中心对称图形的概念即可求解.
【详解】
第1个图形,是中心对称图形,符合题意;
第2个图形,不是中心对称图形,不符合题意;
第3个图形,是中心对称图形,符合题意;
第4个图形,不是中心对称图形,不符合题意.
故答案为:2.
【点睛】
本题考查了中心对称图形,掌握好中心对称图形,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
12.
【解析】
【分析】
根据已知条件求出a,b,代入求值即可;
【详解】
∵点与点关于原点对称,
∴,,
∴;
故答案是.
【点睛】
本题主要考查了平面直角坐标系点的对称,准确计算是解题的关键.
13.
【解析】
【分析】
如图,将△MOG绕点M逆时针旋转60°,得到△MPQ,易知△MOP为等边三角形,继而得到点O到三顶点的距离为:ON+OM+OG=ON+OP+PQ,由此可以发现当点N、O、P、Q在同一条直线上时,有ON+OM+OG最小,此时,∠NMQ=75°+60°=135°,过Q作QA⊥NM交NM的延长线于A,利用勾股定理进行求解即可得.
【详解】
如图,将△MOG绕点M逆时针旋转60°,得到△MPQ,
显然△MOP为等边三角形,
∴,OM+OG=OP+PQ,
∴点O到三顶点的距离为:ON+OM+OG=ON+OP+PQ,
∴当点N、O、P、Q在同一条直线上时,有ON+OM+OG最小,
此时,∠NMQ=75°+60°=135°,
过Q作QA⊥NM交NM的延长线于A,则∠MAQ=90°,
∴∠AMQ=180°-∠NMQ=45°,
∵MQ=MG=4,
∴AQ=AM=MQ cos45°=4,
∴NQ=,
故答案为.
【点睛】
本题考查了旋转的性质,最短路径问题,勾股定理,解直角三角形等知识,综合性较强,有一定的难度,正确添加辅助线是解题的关键.
14.
【解析】
【分析】
先求出,由旋转的性质,得到,,则,即可求出旋转角的度数.
【详解】
解:根据题意,
∵,
∴,
由旋转的性质,则,,
∴,
∴;
∴旋转角的度数是50°;
故答案为:50°.
【点睛】
本题考查了旋转的性质,三角形的内角和定理,解题的关键是熟练掌握旋转的性质进行计算.
15.
【解析】
【分析】
(1)可作点C关于射线AM的对称点C1,点C关于射线AN的对称点C2.连接C1C2.利用两点之间线段最短,可得到当B、D两点与C1、C2在同一条直线上时,△BCD的周长最小,最小值为线段C1C2的长.
(2)根据(1)的作图可知四边形AC1CC2的对角互补,结合轴对称可得∠BCD=90°.利用勾股定理得到CB2+CD2=BD2=()2,因为CB+CD=4﹣,可推出CB CD的值,进而求出三角形的面积.
【详解】
(1)∵直线y=与x轴、y轴分别交于C、A两点,把y=0代入,解得x=2,把x=0代入,解得y=2,
∴点C的坐标为(2,0),点A的坐标为(0,2).
∴AC=4.
作点C关于射线AM的对称点C1,点C关于射线AN的对称点C2.由轴对称的性质,可知CD=C1D,CB=C2B.
∴CB+BD+CD=C2B+BD+C1D=C1C2连接AC1、AC2,
可得∠C1AD=∠CAD,∠C2AB=∠CAB,AC1=AC2=AC=4.
∵∠DAB=45°,
∴∠C1AC2=90°.
连接C1C2.,
∵两点之间线段最短,
∴当B、D两点与C1、C2在同一条直线上时,△BCD的周长最小,最小值为线段C1C2的长.
∴△BCD的周长的最小值为4.
故答案为:4.
(2)根据(1)的作图可知四边形AECF的对角互补,其中∠DAB=45°,因此,∠C2CC1=135°.
即∠BCC2+∠DCC1+∠BCD=135°,
∴2∠BCC2+2∠DCC1+2∠BCD=270°①,
∵∠BC2C=∠BCC2,∠DCC1=∠DC1C,∠BC2C+∠DC1C+∠BCC2+∠DCC1+∠BCD=180°,
∴2∠BCC2+2∠DCC1+∠BCD=180°②,
①-②得,∠BCD=90°.
∴CB2+CD2=BD2=()2=,
∵CB+CD=4﹣,
(CB+CD)2=CB2+CD2+2CB CD,
∴2CB CD=(CB+CD)2-(CB2+CD2)=
∴.
故答案为:
【点睛】
本题考查了最短路径和勾股定理及一次函数的性质,解题关键利用轴对称确定最短路径,结合勾股定理来解决问题.
16.或##或
【解析】
【分析】
连接,根据题意可得,当∠ADQ=90°时,分点在线段上和的延长线上,且,勾股定理求得即可.
【详解】
如图,连接,
在Rt△ABC中,∠ACB=90°,,
,,
,
根据题意可得,当∠ADQ=90°时,点在上,且,
,
如图,在中,,
在中,
故答案为:或.
【点睛】
本题考查了旋转的性质,勾股定理,直角三角形斜边上中线的性质,确定点的位置是解题的关键.
17.
【解析】
【分析】
先连接,,作,的垂直平分线交于点,连接,,再由题意得到旋转中心,由旋转的性质即可得到答案.
【详解】
如图,连接,,作,的垂直平分线交于点,连接,,
∵,的垂直平分线交于点,
∴点是旋转中心,
∵,
∴旋转角.
故答案为.
【点睛】
本题考查旋转,解题的关键是掌握旋转的性质.
18.(1)见解析;(2)
【解析】
【分析】
(1)根据“边角边”证,得到即可;
(2)由(1)得,,再根据三角形内角和证明即可.
【详解】
证明: 线段绕点顺时针旋转角得到线段,
,.
,
.
在与中,
.
(2)解: ,
,
又,
,
【点睛】
本题考查了旋转的性质、全等三角形的判定与性质和三角形内角和定理,解题关键是熟练运用全等三角形的判定与性质进行证明.
19.(1)证明见解析;(2)正确,理由见解析
【解析】
【分析】
(1)如图1中,根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行进行解答;
(2)如图2中,作DM⊥BC于M,AN⊥EC交EC的延长线于N.根据旋转的性质可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用“角角边”证明△ACN和△DCM全等,根据全等三角形对应边相等可得AN=DM,然后利用等底等高的三角形的面积相等证明.
【详解】
解:(1)如图1中,∵△DEC绕点C旋转点D恰好落在AB边上,
∴AC=CD,
∵∠BAC=90°﹣∠B=90°﹣30°=60°,
∴△ACD是等边三角形,
∴∠ACD=60°,
又∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE,
∴DE∥AC;
(2)结论正确,
理由如下:如图2中,作DM⊥BC于M,AN⊥EC交EC的延长线于N.
∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,
∴∠ACN=∠DCM,
在△ACN和△DCM中,
,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S△BDC=S△AEC.
【点睛】
本题属于几何变换综合题,主要考查了全等三角形的判定与性质,等边三角形的判定与性质,旋转的性质的综合应用,添加恰当辅助线构造全等三角形是解题的关键.
20.(1)见解析;(2)11
【解析】
【分析】
(1)延长至,使得;延长至,使得;延长至,使得;再连接即得旋转后对应的;
(2)根据平移的规律求出,再连接点,得,将三角形分割乘两个三角形的面积之和,求出公共边的长即可求解.
【详解】
解:(1)延长至,使得;延长至,使得;延长至,使得;再连接即得旋转后对应的,如下图所示:
(2)由题意,,,平移后得到,其中,根据平移的规律知,平移过程是向下和向右分别移动两个单位可得:,
再连接点,得,其中交轴于点,如上图所示:
由得出直线的方程如下:
直线:
当时,,
,
,
故.
【点睛】
本题考查了图象的旋转和平移,求三角形面积,解题的关键是:掌握图象旋转和平移的性质,求不规则三角形面积可以分割为两个规则的三角形面积之和.
21.(1)AM=DF;(2),证明见解析;(3)1或5
【解析】
【分析】
(1)可通过证明,即可利用全等三角形的性质得出结论;
(2)通过作辅助线,构造等边三角形DMN,再通过全等证明出DF=EN,利用等边三角形得出DN=DM,DA=DB,求出AM=BN,即可证明题中三线段之间的关系;
(3)分别讨论当E点在线段BD和DB的延长线上两种情况,利用全等以及等边三角形的相关结论即可求出DF的长.
【详解】
解:(1)AM=DF;
理由:∵菱形 ABCD 中, ∠ABC=120° ,
可得△BCD和△ABD都是等边三角形;
∴BD=BA,∠ DBA=60°,
又由旋转可知ME=MF,∠EMF= 60°,
得△MEF也是等边三角形,
∴EF=EM,∠MEF= 60°,
∴∠MEA=∠FED,
可证:;
∴AM=DF.
(2)结论:
证明:过点作交延长线于.
∵四边形是菱形
∴,
∴
∵
∴
∴是等边三角形
∴,
∵
∴,
∴是等边三角形
∴
∵,
∴是等边三角形
∴,,
∴
∴
∴
即:
∵,
∴
∴.
(3)1或5
当E点在线段BD上时,由(2)知,,
∵AB=6,
∴BD=AD=6,
∵BD=2BE,AD=3AM,
∴BE=3,AM=2,
∴DF=5;
当E点在线段DB的延长线上时,如图所示:
作MN∥AB与DE交于点N,
∵∠MDN=∠DAB=60°,
利用平行线的性质可得出∠DMN=60°,
则△DMN是等边三角形,
∴MN=MD,
又由∠DMN=∠EMF,
∴∠EMN=∠FMD,
∵ME=MF,
∴,
∴DF=EN
∵EN=EB-BN= BD- AM=3- AD=3- 2= 1;
综上可得:DF的长为1或5.
【点睛】
本题涉及到了几何图形的动点问题,综合考查了等边三角形的判定与性质、菱形的性质、全等三角形的判定与性质、旋转的性质等内容,要求学生理解相关概念与性质,能利用相关知识进行边角之间的转化,本题难点在于作辅助线,考查了学生的综合分析的能力,对学生推理分析能力有较高要求.
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
一、单选题
1.已知点与点关于原点对称,则点的坐标( )
A. B. C. D.
2.把四张扑克牌所摆放的顺序与位置如下,小杨同学选取其中一张扑克牌把他颠倒后在放回原来的位置,那么扑克牌的摆放顺序与位置都没变化,那么小杨同学所选的扑克牌是( )
A. B. C. D.
3.如图,矩形ABCD中,AD=2,AB=,对角线AC上有一点G(异于A,C),连接 DG,将△AGD绕点A 逆时针旋转60°得到△AEF,则BF的长为( )
A. B.2 C. D.2
4.如图,在方格纸上建立的平面直角坐标系中,将绕点按顺时针方向旋转90°,得到,则点的坐标为( ).
A. B.
C. D.
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
6.如图,在中,,,,将绕点顺时针旋转度得到,当点的对应点恰好落在边上时,则的长为( )
A.1.6 B.1.8 C.2 D.2.6
7.若P(x,3)与点Q(4,y)关于原点对称,则xy的值是( )
A.12 B.﹣12 C.64 D.﹣64
8.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
9.如图,将绕点逆时针旋转得到,若且于点,则的度数为( )
A. B. C. D.
10.点 A(x,y)在第二象限内,且│x│=2,│y│=3,则点A关于原点对称的点的坐标为( )
A.(-2,3) B.(2,-3) C.(-3,2) D.(3,-2)
二、填空题
11.下列4种图案中,是中心对称图形的有_____个.
12.已知点与点关于原点对称,则的值为_________.
13.问题背景:如图,将绕点逆时针旋转60°得到,与交于点,可推出结论:
问题解决:如图,在中,,,.点是内一点,则点到三个顶点的距离和的最小值是___________
14.如图,将绕点A逆时针旋转角得到,点B的对应点D恰好落在边上,若,则旋转角的度数是______.
15.在平面直角坐标系中,直线分别交x轴、y轴于C、A两点.将射线绕着点A顺时针旋转,得到射线.点D为上的动点,点B为上的动点,点C在的内部.
(1)周长的最小值是____________________;
(2)当的周长取得最小值,且时,的面积为__________.
16.如图,在Rt△ABC中,∠ACB=90°,,点D为AB的中点,点P在AC上,且CP=1,将CP绕点C在平面内旋转,点P的对应点为点Q,连接AQ,DQ.当∠ADQ=90°时,AQ的长为______.
17.如图,在正方形网格中,格点绕某点顺时针旋转角得到格点,点与点,点与点,点与点是对应点,则_____度.
三、解答题
18.如图,等腰三角形中,,.作于点,将线段绕着点顺时针旋转角后得到线段,连接.
(1)求证:;
(2)延长线段,交线段于点.求的度数(用含有的式子表示) .
19.问题情境:
数学活动课上,老师让同学们以“三角形的旋转”为主题开展数学活动,△ABC和△DEC是两个全等的直角三角形纸片,其中∠ACB=∠DCE=90°,∠B=∠E=30°,AB=DE=4.
解决问题:
(1)如图1,智慧小组将△DEC绕点C顺时针旋转,发现当点D恰好落在AB边上时,DE∥AC,请你帮他们证明这个结论;
(2)缜密小组在智慧小组的基础上继续探究,当△DEC绕点C继续旋转到如图2所示的位置时,连接AE、AD、BD,他们提出S△BDC=S△AEC,请你帮他们验证这一结论是否正确,并说明理由.
20.如图,在平面直角坐标中,的顶点坐标分别是,,.
(1)将以为旋转中心旋转,画出旋转后对应的;
(2)将平移后得到,若点的对应点的坐标为,求的面积
21.在菱形中,,点在的延长线上,点是直线上的动点,连接,将线段绕点逆时针得到线段,连接,.
(1)如图1,当点与点重合时,请直接写出线段与的数量关系;
(2)如图2,当点在上时,线段,,之间有怎样的数量关系?请写出结论并给出证明;
(3)当点在直线上时,若,,,请直接写出线段的长.
参考答案:
1.B
【解析】
【分析】
根据关于原点对称点的坐标变化特征直接判断即可.
【详解】
解:点与点关于原点对称,则点的坐标为,
故选:B.
【点睛】
本题考查了关于原点对称点的坐标,解题关键是明确关于原点对称的两个点横纵坐标都互为相反数.
2.D
【解析】
【分析】
根据题意,图形是中心对称图形即可得出答案.
【详解】
由题意可知,图形是中心对称图形,可得答案为D,
故选:D.
【点睛】
本题考查了图形的中心对称的性质,掌握中心图形的性质是解题的关键.
3.A
【解析】
【分析】
过点F作FH⊥BA交BA的延长线于点H,则∠FHA=90°,△AGD绕点A 逆时针旋转60°得到△AEF,得∠FAD=60°,AF=AD=2,又由四边形ABCD是矩形,∠BAD=90°,得到∠FAH=30°,在Rt△AFH中,FH=AF=1,由勾股定理得AH= ,得到BH=AH+AB=2 ,再由勾股定理得BF=.
【详解】
解:如图,过点F作FH⊥BA交BA的延长线于点H,则∠FHA=90°,
∵△AGD绕点A 逆时针旋转60°得到△AEF
∴∠FAD=60°,AF=AD=2,
∵ 四边形ABCD是矩形
∴ ∠BAD=90°
∴∠BAF=∠FAD+ ∠BAD=150°
∴∠FAH=180°-∠BAF=30°
在Rt△AFH中,FH=AF=1
由勾股定理得
AH=
在Rt△BFH中,FH=1,BH=AH+AB=2
由勾股定理得
BF=
故BF的长.
故选:A
【点睛】
本题考查了图形的旋转,矩形的性质,含30度角的直角三角形的性质,勾股定理等知识,解决此题的关键在于作出正确的辅助线.
4.A
【解析】
【分析】
根据网格结构作出旋转后的图形,然后根据平面直角坐标系写出点B′的坐标即可.
【详解】
△A′B′O如图所示,点B′(2,1).
故选A.
【点睛】
本题考查了坐标与图形变化,熟练掌握网格结构,作出图形是解题的关键.
5.B
【解析】
【分析】
利用轴对称图形和中心对称图形的定义逐项判断即可.
【详解】
A.是轴对称图形不是中心对称图形.故A不符合题意.
B.是轴对称图形也是中心对称图形.故B符合题意.
C.是轴对称图形但不是中心对称图形.故C不符合题意.
D.不是中心对称图形也不是轴对称图形.故D不符合题意.
故选:B
【点睛】
本题考查轴对称图形和中心对称图形的定义,根据选项灵活判断其图形是否符合题意是解本题的关键.
6.A
【解析】
【分析】
由将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上,可得AD=AB,又由∠B=60°,可证得△ABD是等边三角形,继而可得BD=AB=2,则可求得答案.
【详解】
由旋转的性质可知,,
∵,,
∴为等边三角形,
∴,
∴,
故选A.
【点睛】
此题考查旋转的性质,解题关键在于利用旋转的性质得出AD=AB
7.A
【解析】
【分析】
直接利用关于原点对称点的性质得出x,y的值,进而得出答案.
【详解】
∵与点关于原点对称,
∴,,
∴.
故选A.
【点睛】
此题主要考查了关于原点对称点的性质,正确记忆横纵坐标的符号是解题关键.
8.C
【解析】
【分析】
根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.
【详解】
解:A.是轴对称图形,不是中心对称图形,故本选项不符合题意;
B.既不是轴对称图形,又不是中心对称图形,故本选项不符合题意;
C.既是轴对称图形,又是中心对称图形,故本选项符合题意;
D.不是轴对称图形,是中心对称图形,故本选项不符合题意.
故选:C.
【点睛】
本题考查了中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
9.C
【解析】
【分析】
由旋转的性质可得∠BAD=55°,∠E=∠ACB=70°,由直角三角形的性质可得∠DAC=20°,即可求解.
【详解】
解:∵将△ABC绕点A逆时针旋转55°得△ADE,
∴∠BAD=55°,∠E=∠ACB=70°,
∵AD⊥BC,
∴∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=75°.
故选C.
【点睛】
本题考查了旋转的性质,掌握旋转的性质是本题的关键.
10.B
【解析】
【分析】
根据A(x,y)在第二象限内可以判断x,y的符号,再根据|x|=2,|y|=3就可以确定点A的坐标,进而确定点A关于原点的对称点的坐标.
【详解】
∵A(x,y)在第二象限内,
∴x<0 y>0,
又∵|x|=2,|y|=3,
∴x=-2, y=3,
∴点A关于原点的对称点的坐标是(2,-3).
故选:B.
【点睛】
本题考查了关于原点对称的点的坐标,由点所在的象限能判断出坐标的符号,同时考查了关于原点对称的点坐标之间的关系,难度一般.
11.2
【解析】
【分析】
根据中心对称图形的概念即可求解.
【详解】
第1个图形,是中心对称图形,符合题意;
第2个图形,不是中心对称图形,不符合题意;
第3个图形,是中心对称图形,符合题意;
第4个图形,不是中心对称图形,不符合题意.
故答案为:2.
【点睛】
本题考查了中心对称图形,掌握好中心对称图形,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
12.
【解析】
【分析】
根据已知条件求出a,b,代入求值即可;
【详解】
∵点与点关于原点对称,
∴,,
∴;
故答案是.
【点睛】
本题主要考查了平面直角坐标系点的对称,准确计算是解题的关键.
13.
【解析】
【分析】
如图,将△MOG绕点M逆时针旋转60°,得到△MPQ,易知△MOP为等边三角形,继而得到点O到三顶点的距离为:ON+OM+OG=ON+OP+PQ,由此可以发现当点N、O、P、Q在同一条直线上时,有ON+OM+OG最小,此时,∠NMQ=75°+60°=135°,过Q作QA⊥NM交NM的延长线于A,利用勾股定理进行求解即可得.
【详解】
如图,将△MOG绕点M逆时针旋转60°,得到△MPQ,
显然△MOP为等边三角形,
∴,OM+OG=OP+PQ,
∴点O到三顶点的距离为:ON+OM+OG=ON+OP+PQ,
∴当点N、O、P、Q在同一条直线上时,有ON+OM+OG最小,
此时,∠NMQ=75°+60°=135°,
过Q作QA⊥NM交NM的延长线于A,则∠MAQ=90°,
∴∠AMQ=180°-∠NMQ=45°,
∵MQ=MG=4,
∴AQ=AM=MQ cos45°=4,
∴NQ=,
故答案为.
【点睛】
本题考查了旋转的性质,最短路径问题,勾股定理,解直角三角形等知识,综合性较强,有一定的难度,正确添加辅助线是解题的关键.
14.
【解析】
【分析】
先求出,由旋转的性质,得到,,则,即可求出旋转角的度数.
【详解】
解:根据题意,
∵,
∴,
由旋转的性质,则,,
∴,
∴;
∴旋转角的度数是50°;
故答案为:50°.
【点睛】
本题考查了旋转的性质,三角形的内角和定理,解题的关键是熟练掌握旋转的性质进行计算.
15.
【解析】
【分析】
(1)可作点C关于射线AM的对称点C1,点C关于射线AN的对称点C2.连接C1C2.利用两点之间线段最短,可得到当B、D两点与C1、C2在同一条直线上时,△BCD的周长最小,最小值为线段C1C2的长.
(2)根据(1)的作图可知四边形AC1CC2的对角互补,结合轴对称可得∠BCD=90°.利用勾股定理得到CB2+CD2=BD2=()2,因为CB+CD=4﹣,可推出CB CD的值,进而求出三角形的面积.
【详解】
(1)∵直线y=与x轴、y轴分别交于C、A两点,把y=0代入,解得x=2,把x=0代入,解得y=2,
∴点C的坐标为(2,0),点A的坐标为(0,2).
∴AC=4.
作点C关于射线AM的对称点C1,点C关于射线AN的对称点C2.由轴对称的性质,可知CD=C1D,CB=C2B.
∴CB+BD+CD=C2B+BD+C1D=C1C2连接AC1、AC2,
可得∠C1AD=∠CAD,∠C2AB=∠CAB,AC1=AC2=AC=4.
∵∠DAB=45°,
∴∠C1AC2=90°.
连接C1C2.,
∵两点之间线段最短,
∴当B、D两点与C1、C2在同一条直线上时,△BCD的周长最小,最小值为线段C1C2的长.
∴△BCD的周长的最小值为4.
故答案为:4.
(2)根据(1)的作图可知四边形AECF的对角互补,其中∠DAB=45°,因此,∠C2CC1=135°.
即∠BCC2+∠DCC1+∠BCD=135°,
∴2∠BCC2+2∠DCC1+2∠BCD=270°①,
∵∠BC2C=∠BCC2,∠DCC1=∠DC1C,∠BC2C+∠DC1C+∠BCC2+∠DCC1+∠BCD=180°,
∴2∠BCC2+2∠DCC1+∠BCD=180°②,
①-②得,∠BCD=90°.
∴CB2+CD2=BD2=()2=,
∵CB+CD=4﹣,
(CB+CD)2=CB2+CD2+2CB CD,
∴2CB CD=(CB+CD)2-(CB2+CD2)=
∴.
故答案为:
【点睛】
本题考查了最短路径和勾股定理及一次函数的性质,解题关键利用轴对称确定最短路径,结合勾股定理来解决问题.
16.或##或
【解析】
【分析】
连接,根据题意可得,当∠ADQ=90°时,分点在线段上和的延长线上,且,勾股定理求得即可.
【详解】
如图,连接,
在Rt△ABC中,∠ACB=90°,,
,,
,
根据题意可得,当∠ADQ=90°时,点在上,且,
,
如图,在中,,
在中,
故答案为:或.
【点睛】
本题考查了旋转的性质,勾股定理,直角三角形斜边上中线的性质,确定点的位置是解题的关键.
17.
【解析】
【分析】
先连接,,作,的垂直平分线交于点,连接,,再由题意得到旋转中心,由旋转的性质即可得到答案.
【详解】
如图,连接,,作,的垂直平分线交于点,连接,,
∵,的垂直平分线交于点,
∴点是旋转中心,
∵,
∴旋转角.
故答案为.
【点睛】
本题考查旋转,解题的关键是掌握旋转的性质.
18.(1)见解析;(2)
【解析】
【分析】
(1)根据“边角边”证,得到即可;
(2)由(1)得,,再根据三角形内角和证明即可.
【详解】
证明: 线段绕点顺时针旋转角得到线段,
,.
,
.
在与中,
.
(2)解: ,
,
又,
,
【点睛】
本题考查了旋转的性质、全等三角形的判定与性质和三角形内角和定理,解题关键是熟练运用全等三角形的判定与性质进行证明.
19.(1)证明见解析;(2)正确,理由见解析
【解析】
【分析】
(1)如图1中,根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行进行解答;
(2)如图2中,作DM⊥BC于M,AN⊥EC交EC的延长线于N.根据旋转的性质可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用“角角边”证明△ACN和△DCM全等,根据全等三角形对应边相等可得AN=DM,然后利用等底等高的三角形的面积相等证明.
【详解】
解:(1)如图1中,∵△DEC绕点C旋转点D恰好落在AB边上,
∴AC=CD,
∵∠BAC=90°﹣∠B=90°﹣30°=60°,
∴△ACD是等边三角形,
∴∠ACD=60°,
又∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE,
∴DE∥AC;
(2)结论正确,
理由如下:如图2中,作DM⊥BC于M,AN⊥EC交EC的延长线于N.
∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,
∴∠ACN=∠DCM,
在△ACN和△DCM中,
,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S△BDC=S△AEC.
【点睛】
本题属于几何变换综合题,主要考查了全等三角形的判定与性质,等边三角形的判定与性质,旋转的性质的综合应用,添加恰当辅助线构造全等三角形是解题的关键.
20.(1)见解析;(2)11
【解析】
【分析】
(1)延长至,使得;延长至,使得;延长至,使得;再连接即得旋转后对应的;
(2)根据平移的规律求出,再连接点,得,将三角形分割乘两个三角形的面积之和,求出公共边的长即可求解.
【详解】
解:(1)延长至,使得;延长至,使得;延长至,使得;再连接即得旋转后对应的,如下图所示:
(2)由题意,,,平移后得到,其中,根据平移的规律知,平移过程是向下和向右分别移动两个单位可得:,
再连接点,得,其中交轴于点,如上图所示:
由得出直线的方程如下:
直线:
当时,,
,
,
故.
【点睛】
本题考查了图象的旋转和平移,求三角形面积,解题的关键是:掌握图象旋转和平移的性质,求不规则三角形面积可以分割为两个规则的三角形面积之和.
21.(1)AM=DF;(2),证明见解析;(3)1或5
【解析】
【分析】
(1)可通过证明,即可利用全等三角形的性质得出结论;
(2)通过作辅助线,构造等边三角形DMN,再通过全等证明出DF=EN,利用等边三角形得出DN=DM,DA=DB,求出AM=BN,即可证明题中三线段之间的关系;
(3)分别讨论当E点在线段BD和DB的延长线上两种情况,利用全等以及等边三角形的相关结论即可求出DF的长.
【详解】
解:(1)AM=DF;
理由:∵菱形 ABCD 中, ∠ABC=120° ,
可得△BCD和△ABD都是等边三角形;
∴BD=BA,∠ DBA=60°,
又由旋转可知ME=MF,∠EMF= 60°,
得△MEF也是等边三角形,
∴EF=EM,∠MEF= 60°,
∴∠MEA=∠FED,
可证:;
∴AM=DF.
(2)结论:
证明:过点作交延长线于.
∵四边形是菱形
∴,
∴
∵
∴
∴是等边三角形
∴,
∵
∴,
∴是等边三角形
∴
∵,
∴是等边三角形
∴,,
∴
∴
∴
即:
∵,
∴
∴.
(3)1或5
当E点在线段BD上时,由(2)知,,
∵AB=6,
∴BD=AD=6,
∵BD=2BE,AD=3AM,
∴BE=3,AM=2,
∴DF=5;
当E点在线段DB的延长线上时,如图所示:
作MN∥AB与DE交于点N,
∵∠MDN=∠DAB=60°,
利用平行线的性质可得出∠DMN=60°,
则△DMN是等边三角形,
∴MN=MD,
又由∠DMN=∠EMF,
∴∠EMN=∠FMD,
∵ME=MF,
∴,
∴DF=EN
∵EN=EB-BN= BD- AM=3- AD=3- 2= 1;
综上可得:DF的长为1或5.
【点睛】
本题涉及到了几何图形的动点问题,综合考查了等边三角形的判定与性质、菱形的性质、全等三角形的判定与性质、旋转的性质等内容,要求学生理解相关概念与性质,能利用相关知识进行边角之间的转化,本题难点在于作辅助线,考查了学生的综合分析的能力,对学生推理分析能力有较高要求.
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
同课章节目录
