第24章《圆》【挑战满分】2022-2023学年数学九上阶段性复习精选精练(人教版 含解析)
文档属性
| 名称 | 第24章《圆》【挑战满分】2022-2023学年数学九上阶段性复习精选精练(人教版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-29 21:58:18 | ||
图片预览


文档简介
第24章《圆》
一、单选题
1.如图,在由边长为1的7个正六边形组成的网格中,点A,B在格点上.若再选择一个格点C,使△ABC是直角三角形,且每个直角三角形边长均大于1,则符合条件的格点C的个数是( )
A.2 B.4 C.5 D.6
2.如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是( )
A.120° B.125° C.130° D.135°
3.已知每个网格中小正方形的边长都是1,如图中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成,则阴影部分的面积是( )
A. B.π﹣2 C.1+ D.1﹣
4.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )
A.55° B.65° C.60° D.75°
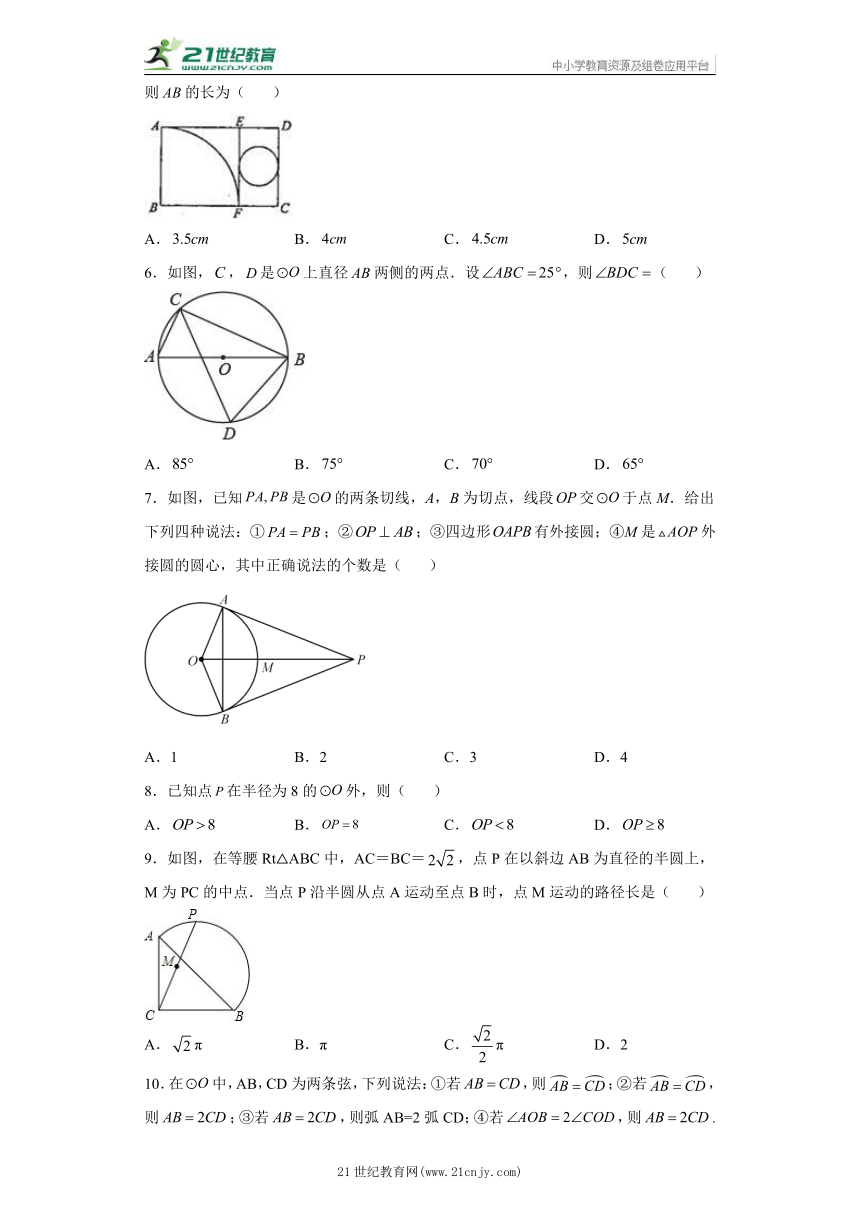
5.如图所示,矩形纸片中,,把它分割成正方形纸片和矩形纸片后,分别裁出扇形和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则的长为( )
A. B. C. D.
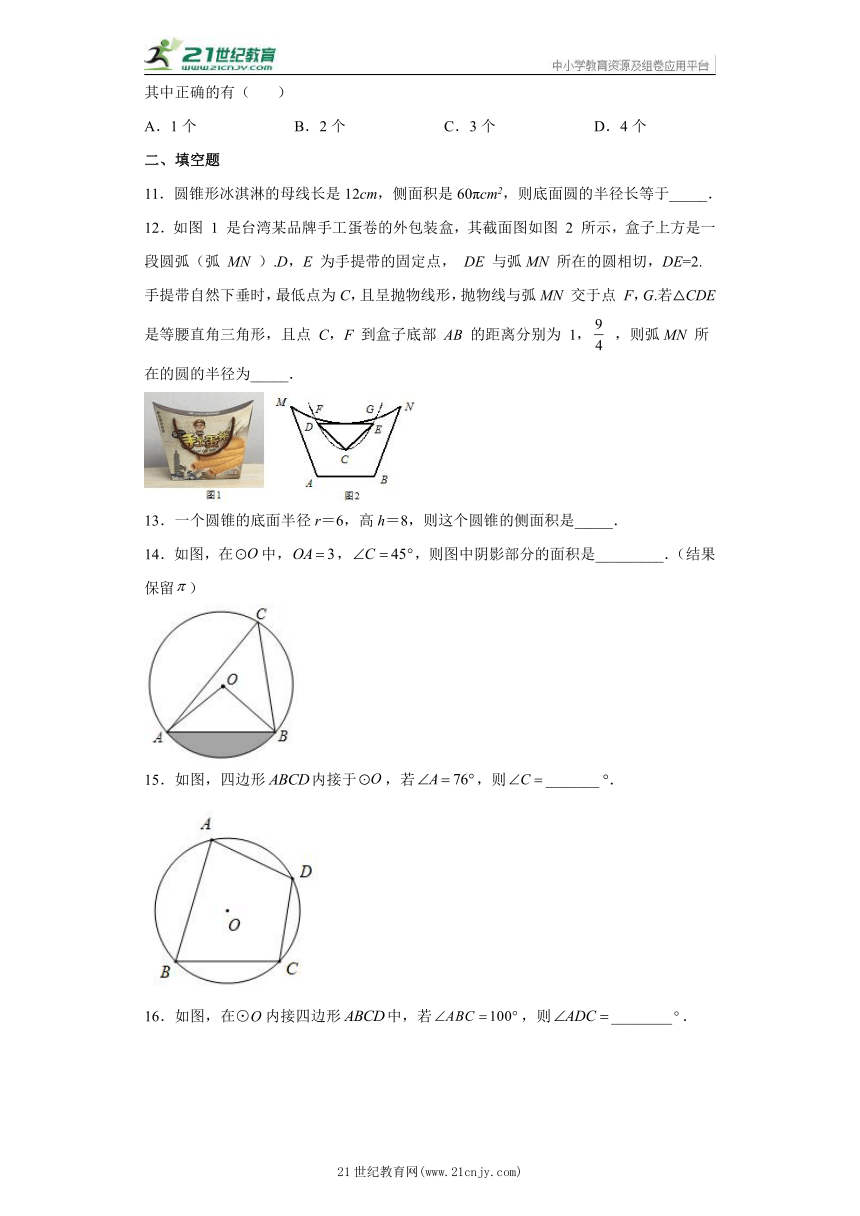
6.如图,,是上直径两侧的两点.设,则( )
A. B. C. D.
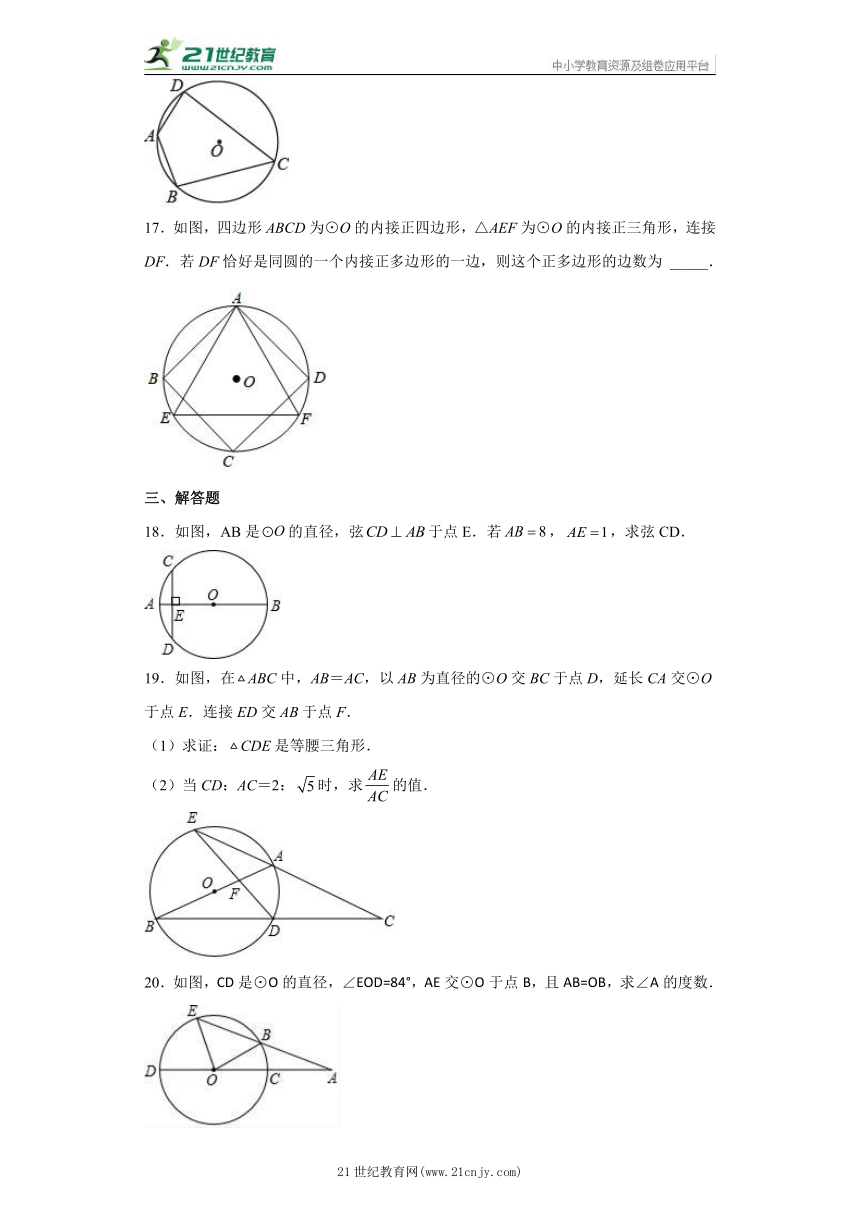
7.如图,已知是的两条切线,A,B为切点,线段交于点M.给出下列四种说法:①;②;③四边形有外接圆;④M是外接圆的圆心,其中正确说法的个数是( )
A.1 B.2 C.3 D.4
8.已知点在半径为8的外,则( )
A. B. C. D.
9.如图,在等腰Rt△ABC中,AC=BC=,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
A.π B.π C.π D.2
10.在中,AB,CD为两条弦,下列说法:①若,则;②若,则;③若,则弧AB=2弧CD;④若,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.圆锥形冰淇淋的母线长是12cm,侧面积是60πcm2,则底面圆的半径长等于_____.
12.如图 1 是台湾某品牌手工蛋卷的外包装盒,其截面图如图 2 所示,盒子上方是一段圆弧(弧 MN ).D,E 为手提带的固定点, DE 与弧MN 所在的圆相切,DE=2.手提带自然下垂时,最低点为C,且呈抛物线形,抛物线与弧MN 交于点 F,G.若△CDE 是等腰直角三角形,且点 C,F 到盒子底部 AB 的距离分别为 1, ,则弧MN 所在的圆的半径为_____.
13.一个圆锥的底面半径r=6,高h=8,则这个圆锥的侧面积是_____.
14.如图,在中,,,则图中阴影部分的面积是_________.(结果保留)
15.如图,四边形内接于,若,则_______ °.
16.如图,在⊙O内接四边形中,若,则________.
17.如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,连接DF.若DF恰好是同圆的一个内接正多边形的一边,则这个正多边形的边数为 _____.
三、解答题
18.如图,AB是的直径,弦于点E.若,,求弦CD.
19.如图,在ABC中,AB=AC,以AB为直径的⊙O交BC于点D,延长CA交⊙O于点E.连接ED交AB于点F.
(1)求证:CDE是等腰三角形.
(2)当CD:AC=2:时,求的值.
20.如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OB,求∠A的度数.
21.(1)如图①,在△ABC中,,AB=4,AC=3,若AD平分∠BAC交于点,那么点到的距离为 .
(2)如图②,四边形内接于,为直径,点B是半圆的三等分点(弧弧),连接,若平分,且,求四边形的面积.
(3)如图③,为把“十四运”办成一届精彩圆满的体育盛会很多公园都在进行花卉装扮,其中一块圆形场地圆O,设计人员准备在内接四边形ABCD区域内进行花卉图案设计,其余部分方便游客参观,按照设计要求,四边形ABCD满足∠ABC=60°,AB=AD,且AD+DC=10(其中 ),为让游客有更好的观体验,四边形ABCD花卉的区域面积越大越好,那么是否存在面积最大的四边形ABCD?若存在,求出这个最大值,不存在请说明理由.
参考答案:
1.D
【解析】
【分析】
分三种情况讨论,当∠A=90°,或∠B=90°,或∠C=90°时,分别画出符合条件的图形,即可解答.
【详解】
解:分三种情况讨论,当∠A=90°,或∠B=90°,或∠C=90°如图
符合条件的格点C的个数是6个
故选:D.
【点睛】
本题考查正多边形和圆的性质、直角三角形的判定与性质、直径所对的圆周角是90°等知识,是基础考点,掌握相关知识是解题关键.
2.B
【解析】
【分析】
利用内心的性质得∠OBC=∠ABC,∠OCB=∠ACB,再根据三角形内角和计算出∠OBC+∠OCB=55°,然后再利用三角形内角和计算∠BOC的度数.
【详解】
解:∵O是△ABC的内心,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣∠A)=(180°﹣70°)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°.
故选:B.
【点睛】
此题主要考查了三角形内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.
3.B
【解析】
【分析】
如图,标注顶点,连接AB,由图形的对称性可得阴影部分面积=S扇形AOB-S△ABO,从而可得答案.
【详解】
解:标注顶点,连接AB,
由对称性可得:
阴影部分面积=S扇形AOB-S△ABO= .
故选:B.
【点睛】
本题考查的是阴影部分的面积的计算,扇形面积的计算,掌握“图形的对称性”是解本题的关键.
4.B
【解析】
【分析】
连接CD,根据圆内接四边形的性质得到∠CDB=180°﹣∠A=130°,根据垂径定理得到OD⊥BC,求得BD=CD,根据等腰三角形的性质即可得到结论.
【详解】
解:连接CD,
∵∠A=50°,
∴∠CDB=180°﹣∠A=130°,
∵E是边BC的中点,
∴OD⊥BC,
∴BD=CD,
∴∠ODB=∠ODC=∠BDC=65°,
故选:B.
【点睛】
本题考查了圆内接四边形的性质,垂径定理,等腰三角形的性质等知识.正确理解题意是解题的关键.
5.B
【解析】
【分析】
设AB=xcm,则DE=(6-x)cm,根据扇形的弧长等于圆锥底面圆的周长列出方程,求解即可.
【详解】
设,则DE=(6-x)cm,
由题意,得,
解得.
故选B.
【点睛】
本题考查了圆锥的计算,矩形的性质,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
6.D
【解析】
【分析】
先利用直径所对的圆周角是直角得到∠ACB=90°,从而求出∠BAC,再利用同弧所对的圆周角相等即可求出∠BDC.
【详解】
解:∵C ,D是⊙O上直径AB两侧的两点,
∴∠ACB=90°,
∵∠ABC=25°,
∴∠BAC=90°-25°=65°,
∴∠BDC=∠BAC=65°,
故选:D.
【点睛】
本题考查了圆周角定理的推论,即直径所对的圆周角是90°和同弧或等弧所对的圆周角相等,解决本题的关键是牢记相关概念与推论,本题蕴含了属性结合的思想方法.
7.C
【解析】
【分析】
由切线长定理判断①,结合等腰三角形的性质判断②,利用切线的性质与直角三角形的斜边上的中线等于斜边的一半,判断③,利用反证法判断④.
【详解】
如图, 是的两条切线,
故①正确,
故②正确,
是的两条切线,
取的中点,连接,
则
所以:以为圆心,为半径作圆,则共圆,故③正确,
M是外接圆的圆心,
与题干提供的条件不符,故④错误,
综上:正确的说法是个,
故选C.
【点睛】
本题考查的是切线长定理,三角形的外接圆,四边形的外接圆,掌握以上知识是解题的关键.
8.A
【解析】
【分析】
根据点P与⊙O的位置关系即可确定OP的范围.
【详解】
解:∵点P在圆O的外部,
∴点P到圆心O的距离大于8,
故选:A.
【点睛】
本题主要考查点与圆的位置关系,关键是要牢记判断点与圆的位置关系的方法.
9.B
【解析】
【分析】
取AB的中点O、AC的中点E、BC的中点F,连接OC、OP、OM、OE、OF、EF,如图,利用勾股定理得到AB的长,进而可求出OC,OP的长,求得∠CMO=90°,于是得到点M在以OC为直径的圆上,然后根据圆的周长公式计算点M运动的路径长.
【详解】
解:取AB的中点O、AC的中点E、BC的中点F,连接OC、OP、OM、OE、OF、EF,如图,
∵在等腰Rt△ABC中,AC=BC=2,
∴AB=BC=4,
∴OC=OP=AB=2,
∵∠ACB=90°,
∴C在⊙O上,
∵M为PC的中点,
∴OM⊥PC,
∴∠CMO=90°,
∴点M在以OC为直径的圆上,
P点在A点时,M点在E点;P点在B点时,M点在F点.
∵O是AB中点,E是AC中点,
∴OE是△ABC的中位线,
∴OE//BC,OE=BC=,
∴OE⊥AC,
同理OF⊥BC,OF=,
∴四边形CEOF是矩形,
∵OE=OF,
∴四边形CEOF为正方形,EF=OC=2,
∴M点的路径为以EF为直径的半圆,
∴点M运动的路径长=×π×2=π.
故选:B.
【点睛】
本题考查了等腰三角形的性质,勾股定理,正方形的判定与性质,圆周角定理,以及动点的轨迹:点按一定规律运动所形成的图形为点运动的轨迹.解决此题的关键是利用圆周角定理确定M点的轨迹为以EF为直径的半圆.
10.A
【解析】
【分析】
根据圆心角、弧、弦之间的关系解答即可.
【详解】
①若,则,正确;
②若,则,故不正确;
③由不能得到弧AB=2弧CD,故不正确;
④若,则,错误.
故选A.
【点睛】
本题考查了圆心角、弧、弦之间的关系,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对的其余各组量都分别相等.也考查了等腰三角形的性质.
11.5cm.
【解析】
【分析】
设圆锥的底面圆的半径长为rcm,根据圆锥的侧面积公式计算即可.
【详解】
解:设圆锥的底面圆的半径长为rcm.
则×2π r×12=60π,
解得:r=5(cm),
故答案为5cm.
【点睛】
圆锥的侧面积公式是本题的考点,牢记其公式是解题的关键.
12..
【解析】
【分析】
以DE的垂直平分线为y轴,AB所在的直线为x轴建立平面直角坐标系,设抛物线的表达式为y=ax2+1,因为△CDE是等腰直角三角形,DE=2,得点E的坐标为(1,2),可得抛物线的表达式为y=x2+1,把当y代入抛物线表达式,求得MH的长,再在Rt△FHM中,用勾股定理建立方程,求得所在的圆的半径.
【详解】
如图,以DE的垂直平分线为y轴,AB所在的直线为x轴建立平面直角坐标系,设所在的圆的圆心为P,半径为r,过F作y轴的垂线交y轴于H,设抛物线的表达式为y=ax2+1.
∵△CDE是等腰直角三角形,DE=2,∴点E的坐标为(1,2),代入抛物线的表达式,得:2=a+1,a=1,∴抛物线的表达式为y=x2+1,当y时,即,解得:,∴FH.
∵∠FHM=90°,DE与所在的圆相切,∴,解得:,∴所在的圆的半径为.
故答案为.
【点睛】
本题考查了圆的切线的性质,待定系数法求抛物线的表达式,垂径定理.解题的关键是建立合适的平面直角坐标系得出抛物线的表达式.
13.60π
【解析】
【分析】
利用圆锥的侧面积公式:,求出圆锥的母线即可解决问题.
【详解】
解:圆锥的母线,
∴圆锥的侧面积=π×10×6=60π,
故答案为:60π.
【点睛】
本题考查了圆锥的侧面积,勾股定理等知识,解题的关键是记住圆锥的侧面积公式.
14.
【解析】
【分析】
由,根据圆周角定理得出,根据S阴影=S扇形AOB-可得出结论.
【详解】
解:∵,
∴,
∴S阴影=S扇形AOB-
,
故答案为:.
【点睛】
本题主要考查圆周角定理、扇形的面积计算,根据题意求得三角形与扇形的面积是解答此题的关键.
15.104
【解析】
【分析】
根据圆内接四边形的对角互补列式计算即可.
【详解】
解:∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∴∠C=180°﹣∠A
=180°﹣76°
=104°,
故答案为:104.
【点睛】
本题考查的是圆内接四边形的性质,掌握圆内接四边形的对角互补是解题的关键.
16.80
【解析】
【分析】
根据圆内接四边形的性质计算出即可.
【详解】
解:∵ABCD是⊙O的内接四边形,∠ABC=100°,
∴∠ABC+∠ADC=180°,
∴.
故答案为.
【点睛】
本题考查了圆内接四边形的性质、解题的关键是熟练掌握圆内接四边形的性质.
17.12
【解析】
【分析】
连接OA、OD、OF,如图,利用正多边形与圆,分别计算⊙O的内接正四边形与内接正三角形的中心角得到∠AOD=90°,∠AOF=120°,则∠DOF=30°,然后计算即可得到n的值.
【详解】
解:连接OA、OD、OF,如图,设这个正多边形为n边形,
∵AD,AF分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOD==90°,∠AOF==120°,
∴∠DOF=∠AOF-∠AOD=30°,
∴n==12,即DF恰好是同圆内接一个正十二边形的一边.
故答案为:12.
【点睛】
本题考查了正多边形与圆:把一个圆分成n(n是大于2的自然数)等份,依次连接各分点所得的多边形是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆;熟练掌握正多边形的有关概念.
18.
【解析】
【分析】
连接OC,如图,根据垂径定理得到CE=DE,然后利用勾股定理计算出CE,从而得到CD的长.
【详解】
解:连接OC,如图,
∵AB为直径,弦CD⊥AB,
∴CE=DE,
∵AB=8,
∴OA=OC=4,
∴OE=OA-AE=4-1=3,
在Rt△OCE中,CE=,
∴CD=2CE=.
【点睛】
本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
19.(1)见解析;(2)
【解析】
【分析】
(1)由等腰三角形的性质得出∠ABC=∠C,由圆周角定理得出∠AED=∠B,证出∠AED=∠C,即可得出结论;
(2)连接AD,过点D作DH⊥AE于点H,设CD=2x,AC=x,则AD=x,由三角形ADC的面积可得出DH的长,求出AE,则可得出答案.
【详解】
解:(1)证明:∵AB=AC,
∴∠ABC=∠C,
∵∠AED=∠ABC,
∴∠C=∠AED,
∴△CDE是等腰三角形;
(2)如图,连接AD,过点D作DH⊥AE于点H,
设CD=2x,AC=x,
∵AB是直径,
∴∠ADC=90°,
∴AD==x,
∵S△ADC=AD DC=AC DH,
∴DH=,
∵DE=CD,
∴CH=EH==x,
∴AE=2CH﹣AC=x.
∴.
【点睛】
本题考查了等腰三角形的判定与性质,圆周角定理,勾股定理,三角形的面积等知识,熟练掌握圆周角定理是解题的关键.
20.28°
【解析】
【分析】
根据等腰三角形的性质,可得∠A与∠AOB的关系,∠BEO与∠EBO的关系,根据三角形外角的性质,可得关于∠A的方程,根据解方程,可得答案.
【详解】
∵AB=BO,
∴∠BOC=∠A,
∴∠EBO=∠BOC+∠A=2∠A,
而OB=OE,得∠E=∠EBO=2∠A,
∴∠EOD=∠E+∠A=3∠A,
而∠EOD=84°,
∴3∠A=84°,
∴∠A=28°.
【点睛】
本题考查了三角形的性质与圆的相关知识点,解题的关键是熟练的掌握三角形的性质与圆的认识.
21.(1);(2) 四边形ABCD的面积为32;(3)存在 .
【解析】
【分析】
(1)如图,作辅助线,证明AE=DE;证明△BDE∽△BCA ,得到,列出比例式即可解决问题.
(2)(2)连接OB,根据题意得∠AOB=60°,作AE⊥BD,利用解直角三角形可求AB的长,通过解直角三角形分别求出BC,AD,CD的长,再根据面积公式求解即可;
过点A作AN⊥BC于点N,AM⊥DC,交DC的延长线于点M,连接AC,可得,根据面积法求出关于面积的二次函数关系式,根据二次函数的性质求出最值即可.
【详解】
解:如图,过点D作DE⊥AB于点E.
则DE//AC;
∵AD平分∠BAC,∠BAC=90°,
∴∠DAE=45°,∠ADE=90° 45°=45°,
∴AE=DE(设为λ),
则BE=4 λ;
∵DE//AC,
∴△BDE∽△BCA,
∴,即:
解得:λ= ,
∴点D到AC的距离.
(2)连接OB,
∵点B是半圆AC的三等分点(弧AB<弧BC),
∴
∴
∵AC是的直径,
∴
∵BD平分∠ABC
∴
过点A作AE⊥BD于点E,则
∴AE=BE
设AE=BE=x,则
∵BD=BE+DE=
∴x=
∴
∵
∴
∴BC=
∵BD平分∠ABC
∴
∴
∴AD=CD
∵AE⊥DE
∴
∵,
∴
∴
=
=
=32;
(3)过点A作AN⊥BC于点N,AM⊥DC,交DC的延长线于点M,连接AC,
∵AB=AD
∴∠ACB=∠ACD
∴AM=AN
∵∠ADC+∠ABC=180°,∠ADC+∠ADM=180°,
∴∠ABC=∠ADM
又∠ANB=∠AMD=90°,
∴△ABN≌△ADM
∴
∵AN=AM,∠BCA=∠DCA,AC=AC
∴△ACN≌△ACM
∴
∵∠ABC=60°
∴∠ADC=120°
∴∠ADM=60°,∠MAD=30°
设DM=x,则AD=2x,
∴
∵
∴,即
∵抛物线对称轴为x=5
∴当x=4时,有最大值,为
【点睛】
本题属于圆综合题,考查了三角形的面积,解直角三角形,角平分线的性质定理,圆周角定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
一、单选题
1.如图,在由边长为1的7个正六边形组成的网格中,点A,B在格点上.若再选择一个格点C,使△ABC是直角三角形,且每个直角三角形边长均大于1,则符合条件的格点C的个数是( )
A.2 B.4 C.5 D.6
2.如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是( )
A.120° B.125° C.130° D.135°
3.已知每个网格中小正方形的边长都是1,如图中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成,则阴影部分的面积是( )
A. B.π﹣2 C.1+ D.1﹣
4.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )
A.55° B.65° C.60° D.75°
5.如图所示,矩形纸片中,,把它分割成正方形纸片和矩形纸片后,分别裁出扇形和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则的长为( )
A. B. C. D.
6.如图,,是上直径两侧的两点.设,则( )
A. B. C. D.
7.如图,已知是的两条切线,A,B为切点,线段交于点M.给出下列四种说法:①;②;③四边形有外接圆;④M是外接圆的圆心,其中正确说法的个数是( )
A.1 B.2 C.3 D.4
8.已知点在半径为8的外,则( )
A. B. C. D.
9.如图,在等腰Rt△ABC中,AC=BC=,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
A.π B.π C.π D.2
10.在中,AB,CD为两条弦,下列说法:①若,则;②若,则;③若,则弧AB=2弧CD;④若,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.圆锥形冰淇淋的母线长是12cm,侧面积是60πcm2,则底面圆的半径长等于_____.
12.如图 1 是台湾某品牌手工蛋卷的外包装盒,其截面图如图 2 所示,盒子上方是一段圆弧(弧 MN ).D,E 为手提带的固定点, DE 与弧MN 所在的圆相切,DE=2.手提带自然下垂时,最低点为C,且呈抛物线形,抛物线与弧MN 交于点 F,G.若△CDE 是等腰直角三角形,且点 C,F 到盒子底部 AB 的距离分别为 1, ,则弧MN 所在的圆的半径为_____.
13.一个圆锥的底面半径r=6,高h=8,则这个圆锥的侧面积是_____.
14.如图,在中,,,则图中阴影部分的面积是_________.(结果保留)
15.如图,四边形内接于,若,则_______ °.
16.如图,在⊙O内接四边形中,若,则________.
17.如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,连接DF.若DF恰好是同圆的一个内接正多边形的一边,则这个正多边形的边数为 _____.
三、解答题
18.如图,AB是的直径,弦于点E.若,,求弦CD.
19.如图,在ABC中,AB=AC,以AB为直径的⊙O交BC于点D,延长CA交⊙O于点E.连接ED交AB于点F.
(1)求证:CDE是等腰三角形.
(2)当CD:AC=2:时,求的值.
20.如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OB,求∠A的度数.
21.(1)如图①,在△ABC中,,AB=4,AC=3,若AD平分∠BAC交于点,那么点到的距离为 .
(2)如图②,四边形内接于,为直径,点B是半圆的三等分点(弧弧),连接,若平分,且,求四边形的面积.
(3)如图③,为把“十四运”办成一届精彩圆满的体育盛会很多公园都在进行花卉装扮,其中一块圆形场地圆O,设计人员准备在内接四边形ABCD区域内进行花卉图案设计,其余部分方便游客参观,按照设计要求,四边形ABCD满足∠ABC=60°,AB=AD,且AD+DC=10(其中 ),为让游客有更好的观体验,四边形ABCD花卉的区域面积越大越好,那么是否存在面积最大的四边形ABCD?若存在,求出这个最大值,不存在请说明理由.
参考答案:
1.D
【解析】
【分析】
分三种情况讨论,当∠A=90°,或∠B=90°,或∠C=90°时,分别画出符合条件的图形,即可解答.
【详解】
解:分三种情况讨论,当∠A=90°,或∠B=90°,或∠C=90°如图
符合条件的格点C的个数是6个
故选:D.
【点睛】
本题考查正多边形和圆的性质、直角三角形的判定与性质、直径所对的圆周角是90°等知识,是基础考点,掌握相关知识是解题关键.
2.B
【解析】
【分析】
利用内心的性质得∠OBC=∠ABC,∠OCB=∠ACB,再根据三角形内角和计算出∠OBC+∠OCB=55°,然后再利用三角形内角和计算∠BOC的度数.
【详解】
解:∵O是△ABC的内心,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣∠A)=(180°﹣70°)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°.
故选:B.
【点睛】
此题主要考查了三角形内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.
3.B
【解析】
【分析】
如图,标注顶点,连接AB,由图形的对称性可得阴影部分面积=S扇形AOB-S△ABO,从而可得答案.
【详解】
解:标注顶点,连接AB,
由对称性可得:
阴影部分面积=S扇形AOB-S△ABO= .
故选:B.
【点睛】
本题考查的是阴影部分的面积的计算,扇形面积的计算,掌握“图形的对称性”是解本题的关键.
4.B
【解析】
【分析】
连接CD,根据圆内接四边形的性质得到∠CDB=180°﹣∠A=130°,根据垂径定理得到OD⊥BC,求得BD=CD,根据等腰三角形的性质即可得到结论.
【详解】
解:连接CD,
∵∠A=50°,
∴∠CDB=180°﹣∠A=130°,
∵E是边BC的中点,
∴OD⊥BC,
∴BD=CD,
∴∠ODB=∠ODC=∠BDC=65°,
故选:B.
【点睛】
本题考查了圆内接四边形的性质,垂径定理,等腰三角形的性质等知识.正确理解题意是解题的关键.
5.B
【解析】
【分析】
设AB=xcm,则DE=(6-x)cm,根据扇形的弧长等于圆锥底面圆的周长列出方程,求解即可.
【详解】
设,则DE=(6-x)cm,
由题意,得,
解得.
故选B.
【点睛】
本题考查了圆锥的计算,矩形的性质,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
6.D
【解析】
【分析】
先利用直径所对的圆周角是直角得到∠ACB=90°,从而求出∠BAC,再利用同弧所对的圆周角相等即可求出∠BDC.
【详解】
解:∵C ,D是⊙O上直径AB两侧的两点,
∴∠ACB=90°,
∵∠ABC=25°,
∴∠BAC=90°-25°=65°,
∴∠BDC=∠BAC=65°,
故选:D.
【点睛】
本题考查了圆周角定理的推论,即直径所对的圆周角是90°和同弧或等弧所对的圆周角相等,解决本题的关键是牢记相关概念与推论,本题蕴含了属性结合的思想方法.
7.C
【解析】
【分析】
由切线长定理判断①,结合等腰三角形的性质判断②,利用切线的性质与直角三角形的斜边上的中线等于斜边的一半,判断③,利用反证法判断④.
【详解】
如图, 是的两条切线,
故①正确,
故②正确,
是的两条切线,
取的中点,连接,
则
所以:以为圆心,为半径作圆,则共圆,故③正确,
M是外接圆的圆心,
与题干提供的条件不符,故④错误,
综上:正确的说法是个,
故选C.
【点睛】
本题考查的是切线长定理,三角形的外接圆,四边形的外接圆,掌握以上知识是解题的关键.
8.A
【解析】
【分析】
根据点P与⊙O的位置关系即可确定OP的范围.
【详解】
解:∵点P在圆O的外部,
∴点P到圆心O的距离大于8,
故选:A.
【点睛】
本题主要考查点与圆的位置关系,关键是要牢记判断点与圆的位置关系的方法.
9.B
【解析】
【分析】
取AB的中点O、AC的中点E、BC的中点F,连接OC、OP、OM、OE、OF、EF,如图,利用勾股定理得到AB的长,进而可求出OC,OP的长,求得∠CMO=90°,于是得到点M在以OC为直径的圆上,然后根据圆的周长公式计算点M运动的路径长.
【详解】
解:取AB的中点O、AC的中点E、BC的中点F,连接OC、OP、OM、OE、OF、EF,如图,
∵在等腰Rt△ABC中,AC=BC=2,
∴AB=BC=4,
∴OC=OP=AB=2,
∵∠ACB=90°,
∴C在⊙O上,
∵M为PC的中点,
∴OM⊥PC,
∴∠CMO=90°,
∴点M在以OC为直径的圆上,
P点在A点时,M点在E点;P点在B点时,M点在F点.
∵O是AB中点,E是AC中点,
∴OE是△ABC的中位线,
∴OE//BC,OE=BC=,
∴OE⊥AC,
同理OF⊥BC,OF=,
∴四边形CEOF是矩形,
∵OE=OF,
∴四边形CEOF为正方形,EF=OC=2,
∴M点的路径为以EF为直径的半圆,
∴点M运动的路径长=×π×2=π.
故选:B.
【点睛】
本题考查了等腰三角形的性质,勾股定理,正方形的判定与性质,圆周角定理,以及动点的轨迹:点按一定规律运动所形成的图形为点运动的轨迹.解决此题的关键是利用圆周角定理确定M点的轨迹为以EF为直径的半圆.
10.A
【解析】
【分析】
根据圆心角、弧、弦之间的关系解答即可.
【详解】
①若,则,正确;
②若,则,故不正确;
③由不能得到弧AB=2弧CD,故不正确;
④若,则,错误.
故选A.
【点睛】
本题考查了圆心角、弧、弦之间的关系,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对的其余各组量都分别相等.也考查了等腰三角形的性质.
11.5cm.
【解析】
【分析】
设圆锥的底面圆的半径长为rcm,根据圆锥的侧面积公式计算即可.
【详解】
解:设圆锥的底面圆的半径长为rcm.
则×2π r×12=60π,
解得:r=5(cm),
故答案为5cm.
【点睛】
圆锥的侧面积公式是本题的考点,牢记其公式是解题的关键.
12..
【解析】
【分析】
以DE的垂直平分线为y轴,AB所在的直线为x轴建立平面直角坐标系,设抛物线的表达式为y=ax2+1,因为△CDE是等腰直角三角形,DE=2,得点E的坐标为(1,2),可得抛物线的表达式为y=x2+1,把当y代入抛物线表达式,求得MH的长,再在Rt△FHM中,用勾股定理建立方程,求得所在的圆的半径.
【详解】
如图,以DE的垂直平分线为y轴,AB所在的直线为x轴建立平面直角坐标系,设所在的圆的圆心为P,半径为r,过F作y轴的垂线交y轴于H,设抛物线的表达式为y=ax2+1.
∵△CDE是等腰直角三角形,DE=2,∴点E的坐标为(1,2),代入抛物线的表达式,得:2=a+1,a=1,∴抛物线的表达式为y=x2+1,当y时,即,解得:,∴FH.
∵∠FHM=90°,DE与所在的圆相切,∴,解得:,∴所在的圆的半径为.
故答案为.
【点睛】
本题考查了圆的切线的性质,待定系数法求抛物线的表达式,垂径定理.解题的关键是建立合适的平面直角坐标系得出抛物线的表达式.
13.60π
【解析】
【分析】
利用圆锥的侧面积公式:,求出圆锥的母线即可解决问题.
【详解】
解:圆锥的母线,
∴圆锥的侧面积=π×10×6=60π,
故答案为:60π.
【点睛】
本题考查了圆锥的侧面积,勾股定理等知识,解题的关键是记住圆锥的侧面积公式.
14.
【解析】
【分析】
由,根据圆周角定理得出,根据S阴影=S扇形AOB-可得出结论.
【详解】
解:∵,
∴,
∴S阴影=S扇形AOB-
,
故答案为:.
【点睛】
本题主要考查圆周角定理、扇形的面积计算,根据题意求得三角形与扇形的面积是解答此题的关键.
15.104
【解析】
【分析】
根据圆内接四边形的对角互补列式计算即可.
【详解】
解:∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∴∠C=180°﹣∠A
=180°﹣76°
=104°,
故答案为:104.
【点睛】
本题考查的是圆内接四边形的性质,掌握圆内接四边形的对角互补是解题的关键.
16.80
【解析】
【分析】
根据圆内接四边形的性质计算出即可.
【详解】
解:∵ABCD是⊙O的内接四边形,∠ABC=100°,
∴∠ABC+∠ADC=180°,
∴.
故答案为.
【点睛】
本题考查了圆内接四边形的性质、解题的关键是熟练掌握圆内接四边形的性质.
17.12
【解析】
【分析】
连接OA、OD、OF,如图,利用正多边形与圆,分别计算⊙O的内接正四边形与内接正三角形的中心角得到∠AOD=90°,∠AOF=120°,则∠DOF=30°,然后计算即可得到n的值.
【详解】
解:连接OA、OD、OF,如图,设这个正多边形为n边形,
∵AD,AF分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOD==90°,∠AOF==120°,
∴∠DOF=∠AOF-∠AOD=30°,
∴n==12,即DF恰好是同圆内接一个正十二边形的一边.
故答案为:12.
【点睛】
本题考查了正多边形与圆:把一个圆分成n(n是大于2的自然数)等份,依次连接各分点所得的多边形是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆;熟练掌握正多边形的有关概念.
18.
【解析】
【分析】
连接OC,如图,根据垂径定理得到CE=DE,然后利用勾股定理计算出CE,从而得到CD的长.
【详解】
解:连接OC,如图,
∵AB为直径,弦CD⊥AB,
∴CE=DE,
∵AB=8,
∴OA=OC=4,
∴OE=OA-AE=4-1=3,
在Rt△OCE中,CE=,
∴CD=2CE=.
【点睛】
本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.
19.(1)见解析;(2)
【解析】
【分析】
(1)由等腰三角形的性质得出∠ABC=∠C,由圆周角定理得出∠AED=∠B,证出∠AED=∠C,即可得出结论;
(2)连接AD,过点D作DH⊥AE于点H,设CD=2x,AC=x,则AD=x,由三角形ADC的面积可得出DH的长,求出AE,则可得出答案.
【详解】
解:(1)证明:∵AB=AC,
∴∠ABC=∠C,
∵∠AED=∠ABC,
∴∠C=∠AED,
∴△CDE是等腰三角形;
(2)如图,连接AD,过点D作DH⊥AE于点H,
设CD=2x,AC=x,
∵AB是直径,
∴∠ADC=90°,
∴AD==x,
∵S△ADC=AD DC=AC DH,
∴DH=,
∵DE=CD,
∴CH=EH==x,
∴AE=2CH﹣AC=x.
∴.
【点睛】
本题考查了等腰三角形的判定与性质,圆周角定理,勾股定理,三角形的面积等知识,熟练掌握圆周角定理是解题的关键.
20.28°
【解析】
【分析】
根据等腰三角形的性质,可得∠A与∠AOB的关系,∠BEO与∠EBO的关系,根据三角形外角的性质,可得关于∠A的方程,根据解方程,可得答案.
【详解】
∵AB=BO,
∴∠BOC=∠A,
∴∠EBO=∠BOC+∠A=2∠A,
而OB=OE,得∠E=∠EBO=2∠A,
∴∠EOD=∠E+∠A=3∠A,
而∠EOD=84°,
∴3∠A=84°,
∴∠A=28°.
【点睛】
本题考查了三角形的性质与圆的相关知识点,解题的关键是熟练的掌握三角形的性质与圆的认识.
21.(1);(2) 四边形ABCD的面积为32;(3)存在 .
【解析】
【分析】
(1)如图,作辅助线,证明AE=DE;证明△BDE∽△BCA ,得到,列出比例式即可解决问题.
(2)(2)连接OB,根据题意得∠AOB=60°,作AE⊥BD,利用解直角三角形可求AB的长,通过解直角三角形分别求出BC,AD,CD的长,再根据面积公式求解即可;
过点A作AN⊥BC于点N,AM⊥DC,交DC的延长线于点M,连接AC,可得,根据面积法求出关于面积的二次函数关系式,根据二次函数的性质求出最值即可.
【详解】
解:如图,过点D作DE⊥AB于点E.
则DE//AC;
∵AD平分∠BAC,∠BAC=90°,
∴∠DAE=45°,∠ADE=90° 45°=45°,
∴AE=DE(设为λ),
则BE=4 λ;
∵DE//AC,
∴△BDE∽△BCA,
∴,即:
解得:λ= ,
∴点D到AC的距离.
(2)连接OB,
∵点B是半圆AC的三等分点(弧AB<弧BC),
∴
∴
∵AC是的直径,
∴
∵BD平分∠ABC
∴
过点A作AE⊥BD于点E,则
∴AE=BE
设AE=BE=x,则
∵BD=BE+DE=
∴x=
∴
∵
∴
∴BC=
∵BD平分∠ABC
∴
∴
∴AD=CD
∵AE⊥DE
∴
∵,
∴
∴
=
=
=32;
(3)过点A作AN⊥BC于点N,AM⊥DC,交DC的延长线于点M,连接AC,
∵AB=AD
∴∠ACB=∠ACD
∴AM=AN
∵∠ADC+∠ABC=180°,∠ADC+∠ADM=180°,
∴∠ABC=∠ADM
又∠ANB=∠AMD=90°,
∴△ABN≌△ADM
∴
∵AN=AM,∠BCA=∠DCA,AC=AC
∴△ACN≌△ACM
∴
∵∠ABC=60°
∴∠ADC=120°
∴∠ADM=60°,∠MAD=30°
设DM=x,则AD=2x,
∴
∵
∴,即
∵抛物线对称轴为x=5
∴当x=4时,有最大值,为
【点睛】
本题属于圆综合题,考查了三角形的面积,解直角三角形,角平分线的性质定理,圆周角定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
同课章节目录
