2013年卓越大学联盟自主选拔录取学科基础测试物理部分解析
文档属性
| 名称 | 2013年卓越大学联盟自主选拔录取学科基础测试物理部分解析 |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2013-08-30 12:56:13 | ||
图片预览



文档简介
本人声明:本资源属本人原创作品,授予21世纪教育网独家发行。
.2013年卓越大学联盟自主选拔录取学科基础测试物理部分
【试题总评】2013年卓越大学联盟自主招生物理试题覆盖了高中物理必修一、必修二、选修3-1、选修3-2、选修3-4、选修3-5,多数试题难度与高考相当,个别试题综合性强,能力要求较高。
一、填空题
1.Co的衰变方程可以写成Co →Ni++,其中是反电子中微子,反电子中微子不带电,质量可视为零。由衰变方程可知Z=_________。如果静止的Co发生衰变,实验过程中测量衰变产物中Ni和的径迹时,由______________守恒定律可知,Ni和的径迹在同一条直线上。
1.答案:28 动量
解析:根据Co的衰变遵循电荷数守恒可得:27=Z-1,解得Z=28.。 如果静止的Co发生衰变,根据动量守恒定律,Ni和的速度方向相反,径迹在同一条直线上。
2.如图,理想变压器有两个接有电阻的独立副线圈甲、乙,其匝数分别为n1和n2。现测得线圈甲上的电流与电压分别为I1和U1,线圈乙上的电流为I2,则线圈乙上的电压U2= ,原线圈上的输入功率P=______________。
2.答案:U1 I1U1+U1 I2。
解析:由变压器变压公式,==,线圈乙上的电压U2=U1。由理想变压器功率关系可得:原线圈上的输入功率P= I1U1+ I2U2= I1U1+U1 I2。
3.(16分)
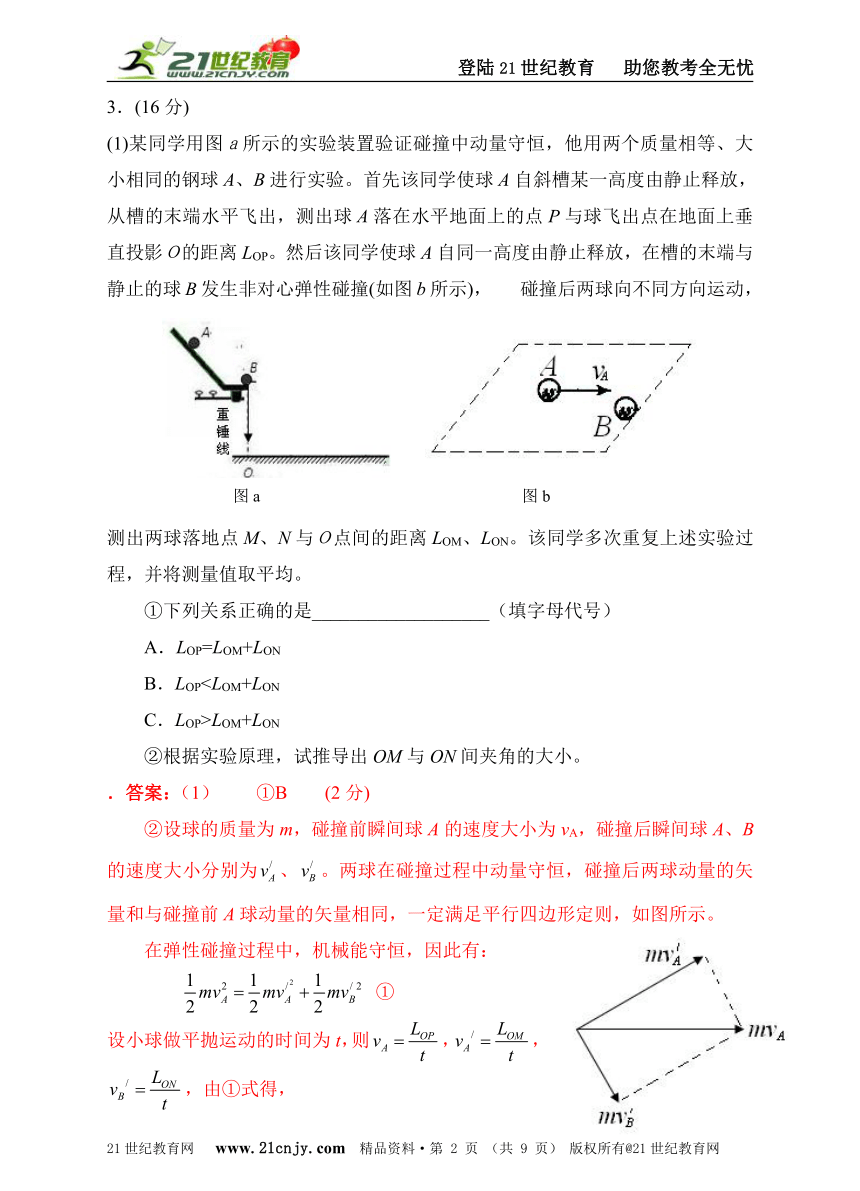
(1)某同学用图a所示的实验装置验证碰撞中动量守恒,他用两个质量相等、大小相同的钢球A、B进行实验。首先该同学使球A自斜槽某一高度由静止释放,从槽的末端水平飞出,测出球A落在水平地面上的点P与球飞出点在地面上垂直投影O的距离LOP。然后该同学使球A自同一高度由静止释放,在槽的末端与静止的球B发生非对心弹性碰撞(如图b所示), 碰撞后两球向不同方向运动,测出两球落地点M、N与O点间的距离LOM、LON。该同学多次重复上述实验过程,并将测量值取平均。
①下列关系正确的是___________________(填字母代号)
A.LOP=LOM+LON
B.LOPC.LOP>LOM+LON
②根据实验原理,试推导出OM与ON间夹角的大小。
.答案:(1) ①B (2分)
②设球的质量为m,碰撞前瞬间球A的速度大小为vA,碰撞后瞬间球A、B的速度大小分别为、。两球在碰撞过程中动量守恒,碰撞后两球动量的矢量和与碰撞前A球动量的矢量相同,一定满足平行四边形定则,如图所示。
在弹性碰撞过程中,机械能守恒,因此有:
①
设小球做平抛运动的时间为t,则,,,由①式得,
②
因此,OM与ON间的夹角为90°。
评分标准:明确说明该过程满足动量守恒得2分,①式2分,②式1分,判断出正确结果得1分。
解析:A与静止的球B发生非对心弹性碰撞,动量守恒,由于二球质量相等,碰撞后二球速度的矢量和等于碰撞前A球速度。而用图a所示的实验装置实验,是用小球的水平位移等效替代小球速度,所以LOP4.(2)用如图所示电路可以测量电源电动势,其中E、EN、Ex分别为工作电源、标准电源和待测电源。R1、R2为电阻箱。R3为滑动变阻器,G为指针可以左右摆动的表头。S1、S3为单刀单掷开关,S2为单刀双掷开关。已知EN=1.018 V,Ex约为1.5 V,E约为4 V。实验过程如下:
I.实验开始前,为保护表头,将滑动变阻器R3的阻值调至最大,R1和R2阻值限定在1000~3000Ω;
II.校准工作电源电动势。将开关S2置于l处,闭合Sl,反复调节电阻R1的阻值,使当S3闭合时,表头的示数为零。减小R3的阻值,通过调整R1的阻值,使表头的示数继续为零,直至R3的阻值为零时,表头示数仍为零;
III.测量待测电源电动势。将开关S2置于2处,在重复上述操作过程中适当调节R2的阻值,使R3的阻值为零时,表头示数为零。
根据上述实验过程回答下列问题:
①在校准工作电源电动势时,测得Rl校和R2校的阻值分别为2931Ω和1069Ω。在测量待测电源电动势的过程中,下列关于RI和R2预估值合理的是___________ (填字母代号)。
A.Rl估=2437Ω,R2估=1463Ω B.RI估=2524Ω,R2估=1376Ω
C.Rl估=2420Ω,R2估=1580Ω D.RI估=2327Ω,R2估=1628Ω
②在测量待测电源电动势的实验过程中,当表头示数为零时,Rl测的读数为2320Ω,此时R2测的阻值应为________Ω, 待测电源电动势的表达式为___________________,根据实验测得的数据计算待测电源电动势为_____________V(结果保留四位有效数字)。
答案:(2) ①CD (2分,选对1个得1分,选错的不得分)
②1680 1.600 (各2分,共6分)
解析:①根据题述E约为4 V,Ex约为1.5 V,R1和R2预估值必须满足大约为或小于,所以选项CD正确。
②由Rl校+R2校=Rl测+R2测,解得R2测=Rl校+R2校-R1=2931Ω+1069Ω-2320Ω=1680Ω.。待测电源电动势的表达式为。根据实验测得的数据计算待测电源电动势为Ex=×1.018V=1.600V..。
5.(12分)如图所示,可视为质点的两物块A、B,质量分别为m、2m,A放在一倾角为30°并固定在水平面上的光滑斜面上,一不可伸长的柔软轻绳跨过光滑轻质定滑轮,两端分别与A、B相连接。托住B使两物块处于静止状态,此时B距地面高度为h,轻绳刚好拉紧,A
和滑轮间的轻绳与斜面平行。现将B从静止释放,斜面足够长。重力加速度为g。求:
(1)B落地前绳中张力的大小T;
(2)整个过程中A沿斜面向上运动的最大距离L。
5. 解析:(1)设B落地前两物块加速度的大小为a,对于A,取沿斜面向上为正;对于B,取竖直向下为正,由牛顿第二定律得
T-mg sin 30°=ma ①
2mg-T=2ma ②
由①②式得 T =mg③
(2)由①②式得:a=g。④
设B落地前瞬间A的速度为v,由运动学公式得
v2=2ah ⑤
设B落地后,A沿斜面运动过程中的加速度为a’,则
a’=-gsin30° ⑥
设B落地后A沿斜面向上运动的最大距离为S,由运动学公式得
-v2=2 a’s ⑦
由④⑤⑥⑦式得
s=h⑧
B自下落开始至落地前瞬间的过程中,A沿斜面运动的距离为h,则整个过程中A沿斜面向上运动的最大距离为 L=s+h=2h ⑨
评分标准:(1)①②式各2分,③式1分,共5分;
(2)⑤⑥式各2分,⑦⑧⑨式各1分,共7分。
6.(14分)如图所示,两根电阻不计的光滑金属导轨竖直放置,相距为L,导轨上端接有阻值为R的电阻,水平条形区域I和II内有磁感应强度为B、方向垂直导轨平面向里的匀强磁场,其宽度均为d,I和II之间相距为h且无磁场。一长度为L、质量为m、电阻不计的导体棒,两端套在导轨上,并与两导轨始终保持良好接触。现将导体棒由区域I上边界H处静止释放,在穿过两段磁场区域的过程中,流过电阻R上的电流及其变化情况相同。重力加速度为g,求:
(1)导体棒进入区域I的瞬间,通过电阻R的电流大小与方向;
(2)导体棒穿过区域I的过程中,电阻R上产生的热量Q;
(3)下面四个图象定性地描述了导体棒速度大小与时间的关系,请选择正确的图象并简述理由。
6 解析:(1)设导体棒进入区域I瞬间的速度大小为v,通过电阻R的电流大小为I,感应电动势为E,由机械能守恒定律得
mgH=mv2, ①
由法拉第电磁感应定律得: E=BLv ②
由闭合电路的欧姆定律得: I=E/R ③
由①②③得: I= ④
由楞次定律可以判断出通过电阻R的电流方向为由右向左。
(2)设导体棒穿出区域I瞬间的速度大小为v’,由能量守恒定律得
mv2+mgd=mv’2+Q ⑤
由题意知,导体棒穿过两段磁场区域过程中,流过电阻R上的电流及其变化情况相同,所以,导体棒在进入区域I和II的瞬间速度相同。导体棒在两磁场之间运动时只受重力作用,由机械能守恒定律得
mv’2+mgh=mv2 ⑥
由⑤⑥式得: Q=mg(h+d) ⑦
(3)选项C正确。
导体棒由静止开始到进入区域I之前,只受重力作用,导体棒做自由落体运动,加速度为g,因此在0~t1时间段内v-t图象为直线。导体棒在两磁场之间运动时也只受重力作用,同理在t2~t3时间段内v-t图象也为直线。
依据题意,两磁场区域宽度d相同,导体棒穿过两段磁场区域过程中,流过电阻R上的电流及其变化情况相同,可知导体棒在进入区域I和II瞬间的速度相同,且在两磁场区域内速度变化相同,因此,导体棒在t1~t2和t3~t4时间段内的v-t图象相同,而且导体棒在磁场区域内的运动为加速度逐渐减小的减速运动(即逐渐减小),所以C是正确的。
评分标准:(1)①②③④式各1分,正确判断出电流方向得1分,共5分;
(2)⑤⑥式各2分,⑦式1分,共5分;
(3)选项正确得2分,能正确清晰解释原因得2分,共4分。
7.(18分)如图所示,可视为质点的三个物块A、B、C质量分别为m1、m2、m3,三物块间有两根轻质弹簧a、b,其原长均为L0,劲度系数分别为ka、kb。a的两端与物块连接,b的两端与物块只接触不连接。a、b被压缩一段距离后,分别由质量忽略不计的硬质连杆锁定,此时b的长度为L,整个装置竖直置于水平地面上,重力加速度为g。
(1)现解开对a的锁定,若当B到达最高点时,A对地面压力恰为零,求此时C距地面的高度H;
(2)在B到达最高点瞬间,解除a与B的连接。并撤走A与a,同时解除对b的锁定。设b恢复形变时间极短,此过程中弹力冲量远大于重力冲量,求C的最大速度的大小v3(弹簧的弹性势能可以表示为,其中为弹簧的形变量);
(3)求C自b解锁瞬间至恢复原长时上升的高度h。
解析:(1)解除a的锁定后,在a的作用下,B、C上升,恢复原长后,弹簧继续伸长,当B到达最高点时,A对地面压力恰为零,设此时a的伸长量为△La,由共点力平衡条件及胡克定律得
ka△La = m1g ①
由H=△La +L0+L
解得H= +L0+L ②
(2)在解除b锁定的瞬间,由于弹簧恢复形变所需的时间极短,弹力远大于重力,因此此过程可视为动量守恒。此时由于B到达最高点,因此B与C的速度均为零,设在b恢复原长时,B的速度大小为v2,取竖直向上为正,由动量守恒定律得
m3v3-m2v2=0 ③
由于b恢复原长所需时间极短,此过程中弹力的冲量远大于重力冲量,因此系统的重 力势能不变,由机械能守恒定律得
m3v32+m2v22= ka (L0-L)2 ④
由③④式得
v3= (L0-L) ⑤
(3)设b从解锁瞬间至恢复原长时所需时间为△t,B高度的变化量为h’,由③式得
m3-m2v2=0 ⑥
由题意知
h+ h’=L0-L ⑦
由⑥⑦式得
h=(L0-L) ⑧
评分标准:(1)①②式各2分,共4分:
(2)③④式各4分,⑤式1分,共9分;
(3)⑥式3分,⑦⑧式各1分,共5分。
.2013年卓越大学联盟自主选拔录取学科基础测试物理部分
【试题总评】2013年卓越大学联盟自主招生物理试题覆盖了高中物理必修一、必修二、选修3-1、选修3-2、选修3-4、选修3-5,多数试题难度与高考相当,个别试题综合性强,能力要求较高。
一、填空题
1.Co的衰变方程可以写成Co →Ni++,其中是反电子中微子,反电子中微子不带电,质量可视为零。由衰变方程可知Z=_________。如果静止的Co发生衰变,实验过程中测量衰变产物中Ni和的径迹时,由______________守恒定律可知,Ni和的径迹在同一条直线上。
1.答案:28 动量
解析:根据Co的衰变遵循电荷数守恒可得:27=Z-1,解得Z=28.。 如果静止的Co发生衰变,根据动量守恒定律,Ni和的速度方向相反,径迹在同一条直线上。
2.如图,理想变压器有两个接有电阻的独立副线圈甲、乙,其匝数分别为n1和n2。现测得线圈甲上的电流与电压分别为I1和U1,线圈乙上的电流为I2,则线圈乙上的电压U2= ,原线圈上的输入功率P=______________。
2.答案:U1 I1U1+U1 I2。
解析:由变压器变压公式,==,线圈乙上的电压U2=U1。由理想变压器功率关系可得:原线圈上的输入功率P= I1U1+ I2U2= I1U1+U1 I2。
3.(16分)
(1)某同学用图a所示的实验装置验证碰撞中动量守恒,他用两个质量相等、大小相同的钢球A、B进行实验。首先该同学使球A自斜槽某一高度由静止释放,从槽的末端水平飞出,测出球A落在水平地面上的点P与球飞出点在地面上垂直投影O的距离LOP。然后该同学使球A自同一高度由静止释放,在槽的末端与静止的球B发生非对心弹性碰撞(如图b所示), 碰撞后两球向不同方向运动,测出两球落地点M、N与O点间的距离LOM、LON。该同学多次重复上述实验过程,并将测量值取平均。
①下列关系正确的是___________________(填字母代号)
A.LOP=LOM+LON
B.LOP
②根据实验原理,试推导出OM与ON间夹角的大小。
.答案:(1) ①B (2分)
②设球的质量为m,碰撞前瞬间球A的速度大小为vA,碰撞后瞬间球A、B的速度大小分别为、。两球在碰撞过程中动量守恒,碰撞后两球动量的矢量和与碰撞前A球动量的矢量相同,一定满足平行四边形定则,如图所示。
在弹性碰撞过程中,机械能守恒,因此有:
①
设小球做平抛运动的时间为t,则,,,由①式得,
②
因此,OM与ON间的夹角为90°。
评分标准:明确说明该过程满足动量守恒得2分,①式2分,②式1分,判断出正确结果得1分。
解析:A与静止的球B发生非对心弹性碰撞,动量守恒,由于二球质量相等,碰撞后二球速度的矢量和等于碰撞前A球速度。而用图a所示的实验装置实验,是用小球的水平位移等效替代小球速度,所以LOP
I.实验开始前,为保护表头,将滑动变阻器R3的阻值调至最大,R1和R2阻值限定在1000~3000Ω;
II.校准工作电源电动势。将开关S2置于l处,闭合Sl,反复调节电阻R1的阻值,使当S3闭合时,表头的示数为零。减小R3的阻值,通过调整R1的阻值,使表头的示数继续为零,直至R3的阻值为零时,表头示数仍为零;
III.测量待测电源电动势。将开关S2置于2处,在重复上述操作过程中适当调节R2的阻值,使R3的阻值为零时,表头示数为零。
根据上述实验过程回答下列问题:
①在校准工作电源电动势时,测得Rl校和R2校的阻值分别为2931Ω和1069Ω。在测量待测电源电动势的过程中,下列关于RI和R2预估值合理的是___________ (填字母代号)。
A.Rl估=2437Ω,R2估=1463Ω B.RI估=2524Ω,R2估=1376Ω
C.Rl估=2420Ω,R2估=1580Ω D.RI估=2327Ω,R2估=1628Ω
②在测量待测电源电动势的实验过程中,当表头示数为零时,Rl测的读数为2320Ω,此时R2测的阻值应为________Ω, 待测电源电动势的表达式为___________________,根据实验测得的数据计算待测电源电动势为_____________V(结果保留四位有效数字)。
答案:(2) ①CD (2分,选对1个得1分,选错的不得分)
②1680 1.600 (各2分,共6分)
解析:①根据题述E约为4 V,Ex约为1.5 V,R1和R2预估值必须满足大约为或小于,所以选项CD正确。
②由Rl校+R2校=Rl测+R2测,解得R2测=Rl校+R2校-R1=2931Ω+1069Ω-2320Ω=1680Ω.。待测电源电动势的表达式为。根据实验测得的数据计算待测电源电动势为Ex=×1.018V=1.600V..。
5.(12分)如图所示,可视为质点的两物块A、B,质量分别为m、2m,A放在一倾角为30°并固定在水平面上的光滑斜面上,一不可伸长的柔软轻绳跨过光滑轻质定滑轮,两端分别与A、B相连接。托住B使两物块处于静止状态,此时B距地面高度为h,轻绳刚好拉紧,A
和滑轮间的轻绳与斜面平行。现将B从静止释放,斜面足够长。重力加速度为g。求:
(1)B落地前绳中张力的大小T;
(2)整个过程中A沿斜面向上运动的最大距离L。
5. 解析:(1)设B落地前两物块加速度的大小为a,对于A,取沿斜面向上为正;对于B,取竖直向下为正,由牛顿第二定律得
T-mg sin 30°=ma ①
2mg-T=2ma ②
由①②式得 T =mg③
(2)由①②式得:a=g。④
设B落地前瞬间A的速度为v,由运动学公式得
v2=2ah ⑤
设B落地后,A沿斜面运动过程中的加速度为a’,则
a’=-gsin30° ⑥
设B落地后A沿斜面向上运动的最大距离为S,由运动学公式得
-v2=2 a’s ⑦
由④⑤⑥⑦式得
s=h⑧
B自下落开始至落地前瞬间的过程中,A沿斜面运动的距离为h,则整个过程中A沿斜面向上运动的最大距离为 L=s+h=2h ⑨
评分标准:(1)①②式各2分,③式1分,共5分;
(2)⑤⑥式各2分,⑦⑧⑨式各1分,共7分。
6.(14分)如图所示,两根电阻不计的光滑金属导轨竖直放置,相距为L,导轨上端接有阻值为R的电阻,水平条形区域I和II内有磁感应强度为B、方向垂直导轨平面向里的匀强磁场,其宽度均为d,I和II之间相距为h且无磁场。一长度为L、质量为m、电阻不计的导体棒,两端套在导轨上,并与两导轨始终保持良好接触。现将导体棒由区域I上边界H处静止释放,在穿过两段磁场区域的过程中,流过电阻R上的电流及其变化情况相同。重力加速度为g,求:
(1)导体棒进入区域I的瞬间,通过电阻R的电流大小与方向;
(2)导体棒穿过区域I的过程中,电阻R上产生的热量Q;
(3)下面四个图象定性地描述了导体棒速度大小与时间的关系,请选择正确的图象并简述理由。
6 解析:(1)设导体棒进入区域I瞬间的速度大小为v,通过电阻R的电流大小为I,感应电动势为E,由机械能守恒定律得
mgH=mv2, ①
由法拉第电磁感应定律得: E=BLv ②
由闭合电路的欧姆定律得: I=E/R ③
由①②③得: I= ④
由楞次定律可以判断出通过电阻R的电流方向为由右向左。
(2)设导体棒穿出区域I瞬间的速度大小为v’,由能量守恒定律得
mv2+mgd=mv’2+Q ⑤
由题意知,导体棒穿过两段磁场区域过程中,流过电阻R上的电流及其变化情况相同,所以,导体棒在进入区域I和II的瞬间速度相同。导体棒在两磁场之间运动时只受重力作用,由机械能守恒定律得
mv’2+mgh=mv2 ⑥
由⑤⑥式得: Q=mg(h+d) ⑦
(3)选项C正确。
导体棒由静止开始到进入区域I之前,只受重力作用,导体棒做自由落体运动,加速度为g,因此在0~t1时间段内v-t图象为直线。导体棒在两磁场之间运动时也只受重力作用,同理在t2~t3时间段内v-t图象也为直线。
依据题意,两磁场区域宽度d相同,导体棒穿过两段磁场区域过程中,流过电阻R上的电流及其变化情况相同,可知导体棒在进入区域I和II瞬间的速度相同,且在两磁场区域内速度变化相同,因此,导体棒在t1~t2和t3~t4时间段内的v-t图象相同,而且导体棒在磁场区域内的运动为加速度逐渐减小的减速运动(即逐渐减小),所以C是正确的。
评分标准:(1)①②③④式各1分,正确判断出电流方向得1分,共5分;
(2)⑤⑥式各2分,⑦式1分,共5分;
(3)选项正确得2分,能正确清晰解释原因得2分,共4分。
7.(18分)如图所示,可视为质点的三个物块A、B、C质量分别为m1、m2、m3,三物块间有两根轻质弹簧a、b,其原长均为L0,劲度系数分别为ka、kb。a的两端与物块连接,b的两端与物块只接触不连接。a、b被压缩一段距离后,分别由质量忽略不计的硬质连杆锁定,此时b的长度为L,整个装置竖直置于水平地面上,重力加速度为g。
(1)现解开对a的锁定,若当B到达最高点时,A对地面压力恰为零,求此时C距地面的高度H;
(2)在B到达最高点瞬间,解除a与B的连接。并撤走A与a,同时解除对b的锁定。设b恢复形变时间极短,此过程中弹力冲量远大于重力冲量,求C的最大速度的大小v3(弹簧的弹性势能可以表示为,其中为弹簧的形变量);
(3)求C自b解锁瞬间至恢复原长时上升的高度h。
解析:(1)解除a的锁定后,在a的作用下,B、C上升,恢复原长后,弹簧继续伸长,当B到达最高点时,A对地面压力恰为零,设此时a的伸长量为△La,由共点力平衡条件及胡克定律得
ka△La = m1g ①
由H=△La +L0+L
解得H= +L0+L ②
(2)在解除b锁定的瞬间,由于弹簧恢复形变所需的时间极短,弹力远大于重力,因此此过程可视为动量守恒。此时由于B到达最高点,因此B与C的速度均为零,设在b恢复原长时,B的速度大小为v2,取竖直向上为正,由动量守恒定律得
m3v3-m2v2=0 ③
由于b恢复原长所需时间极短,此过程中弹力的冲量远大于重力冲量,因此系统的重 力势能不变,由机械能守恒定律得
m3v32+m2v22= ka (L0-L)2 ④
由③④式得
v3= (L0-L) ⑤
(3)设b从解锁瞬间至恢复原长时所需时间为△t,B高度的变化量为h’,由③式得
m3-m2v2=0 ⑥
由题意知
h+ h’=L0-L ⑦
由⑥⑦式得
h=(L0-L) ⑧
评分标准:(1)①②式各2分,共4分:
(2)③④式各4分,⑤式1分,共9分;
(3)⑥式3分,⑦⑧式各1分,共5分。
同课章节目录
