5.4两角和与差的正弦[下学期]
文档属性
| 名称 | 5.4两角和与差的正弦[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 62.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-27 00:00:00 | ||
图片预览



文档简介
课件9张PPT。两角和与差的正弦执教者:丁良统复习 两角和与差的余弦公式
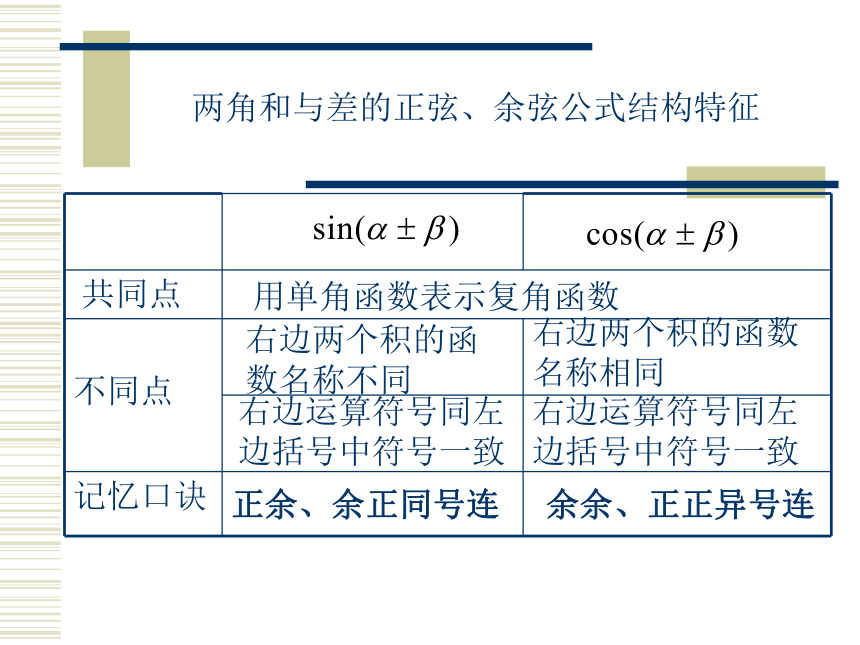
已知 、 两角,我们可以利用 、 的三角函数去计算复合角 ± 的余弦,那么,我们能否用的 、 三角函数去表达复合角 ± 的正弦呢 ?诱导公式:两角和与差的正弦、余弦公式结构特征 用单角函数表示复角函数右边两个积的函数名称不同右边运算符号同左边括号中符号一致正余、余正同号连 右边两个积的函数名称相同右边运算符号同左边括号中符号一致余余、正正异号连利用公式判断下列各题:(1)cos(15°+30°) =cos15°cos30°+sin15°sin30° ( )
(2)cos(15°+30°)=cos15°sin30°-sin15°cos30° ( )
(3)sin(15°+30°)=sin15°sin30°+cos15°cos30° ( )
(4)sin(15°+30°)=sin15°cos30°-cos15°sin30° ( )
(5)sin(15°-30°)=sin15°cos30°-cos15°sin30° ( )√××××例题 例1:求下列各三角函数的精确值
①sin75° ②cos75° ③sin15°
例2:化简:练习:试一试,看谁快:①sin13°cos17°+cos13°sin17°=
②sin70°cos25°-sin25°cos70°=
③sin7°cos37°-sin83°sin37°=
④sin20°cos50°-sin70°cos40°=
⑤sin( + )·cos -cos( + )sin =
⑥已知sin = , ∈( ,π),求sin( + )=?
?
⑦已知sin = , cos =- ,且 、 都为第二象限角,求sin( - )=? 探索中发现: ①单位圆⊙o,∠xop= ,则圆上点p的坐标( )
②点p绕原点旋转角到p’位置,则p’的坐标( )
③若cos = ,sin = , =45°,则p’的坐标为( )
④若把圆的半径扩大到原来5倍,则p的坐标为 ,p'的坐标为 )
。(课堂小结
S( ± ) :sin( ± )= sin · cos ± cos ·sin
:
1、 用单角函数表示复角函数,
2、右边两个积的函数名称不同,
3、右边运算符号同左边括号中符号一致。
记忆口诀:正余、余正同号连(3)注意公式的逆用和顺用,要求熟练地把公式中的右式化为左式。及和角公式在实际生活中应用(1)两角和与差的正弦公式(2)公式结构特点作业:1、探索:和角公式与诱导公式之间的关系
2、课后练习:1、2、3、4
已知 、 两角,我们可以利用 、 的三角函数去计算复合角 ± 的余弦,那么,我们能否用的 、 三角函数去表达复合角 ± 的正弦呢 ?诱导公式:两角和与差的正弦、余弦公式结构特征 用单角函数表示复角函数右边两个积的函数名称不同右边运算符号同左边括号中符号一致正余、余正同号连 右边两个积的函数名称相同右边运算符号同左边括号中符号一致余余、正正异号连利用公式判断下列各题:(1)cos(15°+30°) =cos15°cos30°+sin15°sin30° ( )
(2)cos(15°+30°)=cos15°sin30°-sin15°cos30° ( )
(3)sin(15°+30°)=sin15°sin30°+cos15°cos30° ( )
(4)sin(15°+30°)=sin15°cos30°-cos15°sin30° ( )
(5)sin(15°-30°)=sin15°cos30°-cos15°sin30° ( )√××××例题 例1:求下列各三角函数的精确值
①sin75° ②cos75° ③sin15°
例2:化简:练习:试一试,看谁快:①sin13°cos17°+cos13°sin17°=
②sin70°cos25°-sin25°cos70°=
③sin7°cos37°-sin83°sin37°=
④sin20°cos50°-sin70°cos40°=
⑤sin( + )·cos -cos( + )sin =
⑥已知sin = , ∈( ,π),求sin( + )=?
?
⑦已知sin = , cos =- ,且 、 都为第二象限角,求sin( - )=? 探索中发现: ①单位圆⊙o,∠xop= ,则圆上点p的坐标( )
②点p绕原点旋转角到p’位置,则p’的坐标( )
③若cos = ,sin = , =45°,则p’的坐标为( )
④若把圆的半径扩大到原来5倍,则p的坐标为 ,p'的坐标为 )
。(课堂小结
S( ± ) :sin( ± )= sin · cos ± cos ·sin
:
1、 用单角函数表示复角函数,
2、右边两个积的函数名称不同,
3、右边运算符号同左边括号中符号一致。
记忆口诀:正余、余正同号连(3)注意公式的逆用和顺用,要求熟练地把公式中的右式化为左式。及和角公式在实际生活中应用(1)两角和与差的正弦公式(2)公式结构特点作业:1、探索:和角公式与诱导公式之间的关系
2、课后练习:1、2、3、4
