高中数学课件/两角和与差的三角函数(2)[下学期]
文档属性
| 名称 | 高中数学课件/两角和与差的三角函数(2)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 156.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-12 20:03:00 | ||
图片预览


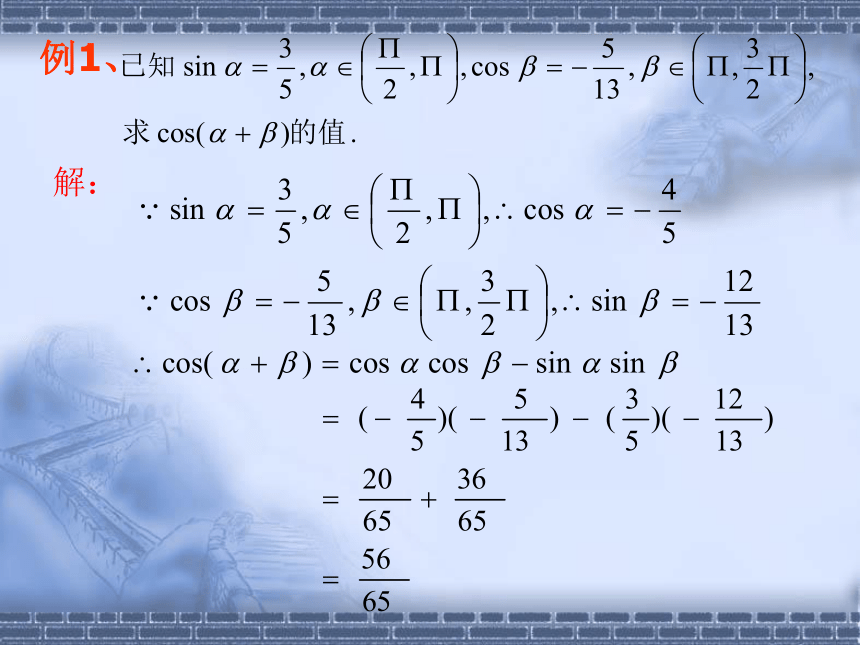



文档简介
课件12张PPT。两角和与差的三角函数(2)山东省嘉祥县第四中学 曾庆坤 手机13153723886
注意: 1。公式中三角符号的顺序 CCSS 2。公式中角的顺序 ? ? ? ? 3。公式中的运算符号 Cα+β:COS(? +?)=COS ? COS ? -Sin ? Sin ?COS(? – ?)=COS ? COS ? +Sin ? Sin ?Cα-β:请同学们回忆两角和与差的余弦公式:例1、解:变式1、已知cos(α–30 °)=15/17, α为大于30 ° 的锐角,求cos α的值.Cα+β:小结:观察公式Cα±β结构特征,
注意符号区别以及公式中角的任意性,
要注意公式既可正用,逆用,还可变用,
如 cos α=cos[(α-β)+β]COS(? +?)=COS ? COS ? -Sin ? Sin ?COS(? – ?)=COS ? COS ? +Sin ? Sin ?Cα-β:例2、证明:公式六 例4.cos25 °cos35 °–cos65 °cos55 °的值等于 ( ). (A) 0 (B) 1/2 (C) √3/2 (D)–1/2
解: 原式=cos25 °cos35 °–sin25 °sin35 °
=cos(25 ° +35 °)
=cos60 °
=1/2.
故选: ( )B 已知: ,
求证: 变式一:变式二:例3、求证: 变式:求 的值; 例3.在△ABC中,cosA=3/5,cosB=5/13,则cosC的 值为( ). 分析: ∵C=180 °–(A+B)
∴cosC=–cos(A+B)= –cosAcosB+sinAsinB
已知cosA=3/5 ,cosB=5/13,尚需求sinA,sinB的值.
∵sinA= 4/5 , sinB=12/13,
∴cosC=–3/5 × 5/13 + 4/5 × 12/13
=33/65.变式:在△ABC中,sinA=3/5,cosB=5/13,则cosC 的值为( ).
注意: 1。公式中三角符号的顺序 CCSS 2。公式中角的顺序 ? ? ? ? 3。公式中的运算符号 Cα+β:COS(? +?)=COS ? COS ? -Sin ? Sin ?COS(? – ?)=COS ? COS ? +Sin ? Sin ?Cα-β:请同学们回忆两角和与差的余弦公式:例1、解:变式1、已知cos(α–30 °)=15/17, α为大于30 ° 的锐角,求cos α的值.Cα+β:小结:观察公式Cα±β结构特征,
注意符号区别以及公式中角的任意性,
要注意公式既可正用,逆用,还可变用,
如 cos α=cos[(α-β)+β]COS(? +?)=COS ? COS ? -Sin ? Sin ?COS(? – ?)=COS ? COS ? +Sin ? Sin ?Cα-β:例2、证明:公式六 例4.cos25 °cos35 °–cos65 °cos55 °的值等于 ( ). (A) 0 (B) 1/2 (C) √3/2 (D)–1/2
解: 原式=cos25 °cos35 °–sin25 °sin35 °
=cos(25 ° +35 °)
=cos60 °
=1/2.
故选: ( )B 已知: ,
求证: 变式一:变式二:例3、求证: 变式:求 的值; 例3.在△ABC中,cosA=3/5,cosB=5/13,则cosC的 值为( ). 分析: ∵C=180 °–(A+B)
∴cosC=–cos(A+B)= –cosAcosB+sinAsinB
已知cosA=3/5 ,cosB=5/13,尚需求sinA,sinB的值.
∵sinA= 4/5 , sinB=12/13,
∴cosC=–3/5 × 5/13 + 4/5 × 12/13
=33/65.变式:在△ABC中,sinA=3/5,cosB=5/13,则cosC 的值为( ).
