两角和与差的余弦[上学期]
图片预览

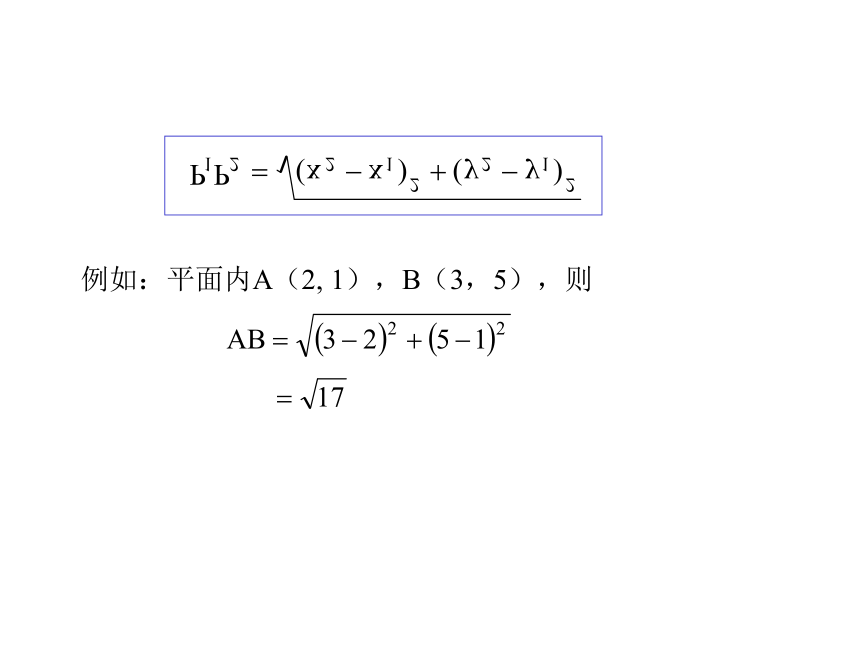
文档简介
课件12张PPT。§4.6.1 两角和与差的余弦 问题 已知任意角α、β的三角函数值,如何求α+β、α-β或2α的三角函数值?
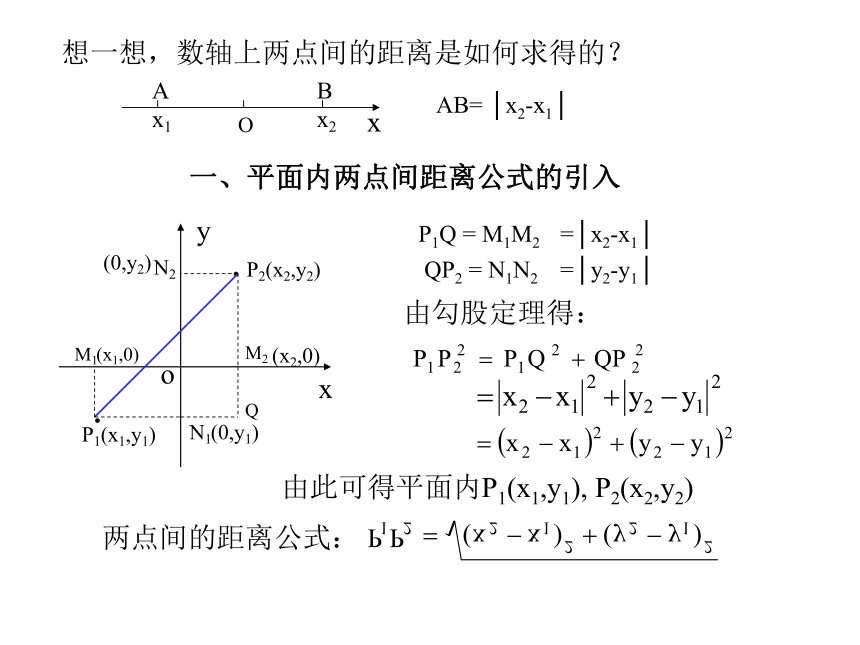
一、平面内两点间距离公式的引入 x.P1(x1,y1)yo.P2(x2,y2)M1M2N1N2(0,y1)(0,y2)Q P1Q = M1M2QP2 = N1N2由勾股定理得: 由此可得平面内P1(x1,y1), P2(x2,y2)(x1,0)(x2,0)
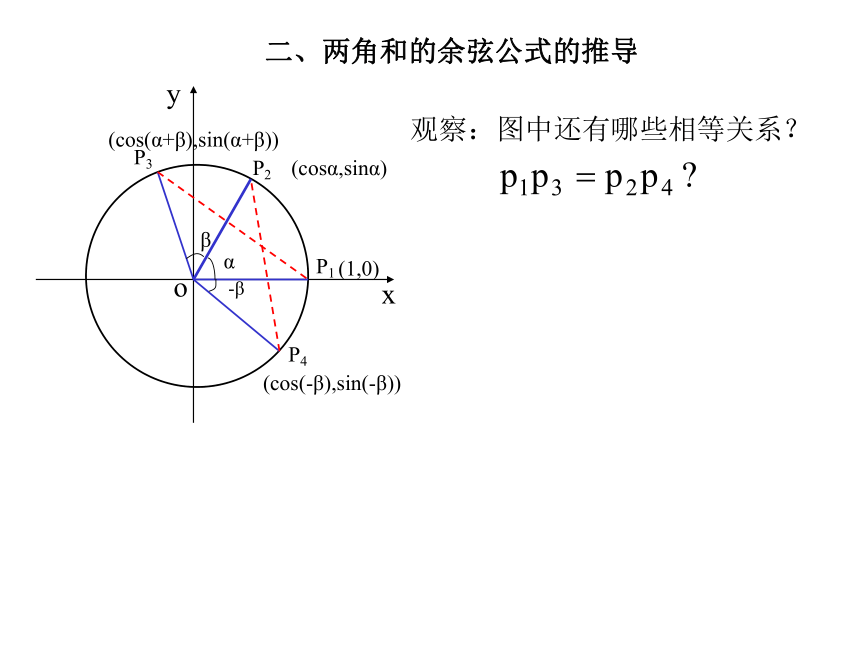
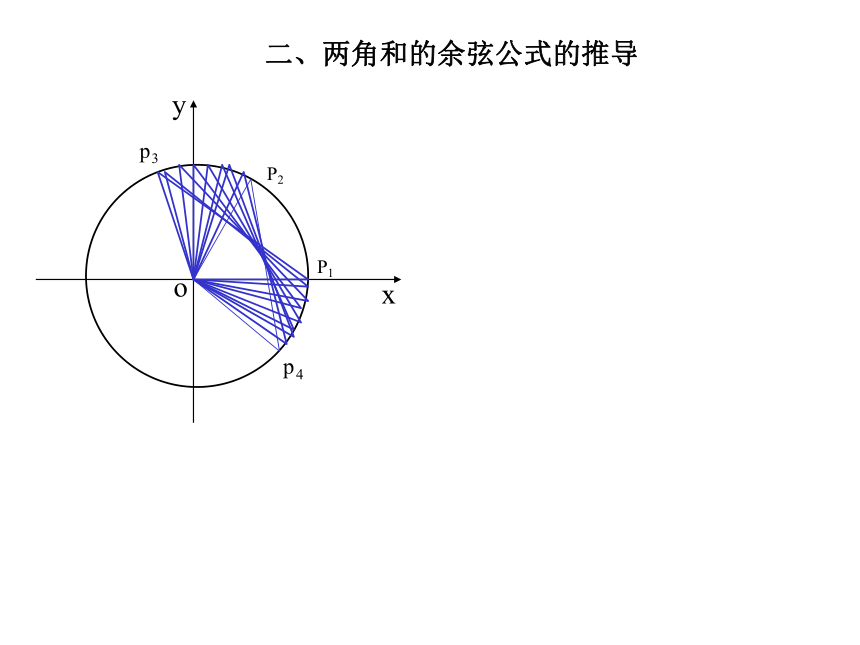
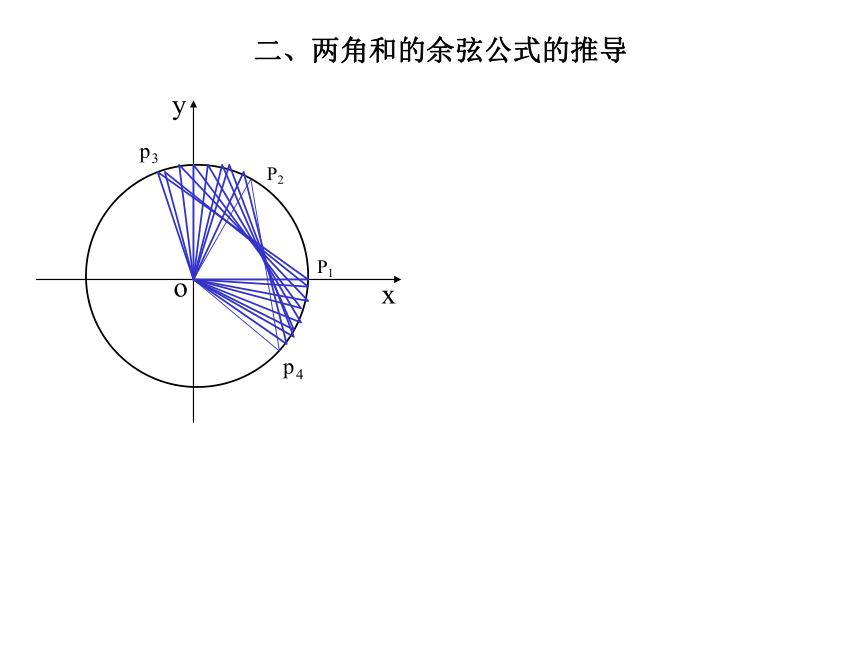
想一想,数轴上两点间的距离是如何求得的?ABOxx1x2 AB=│x2-x1│=│x2-x1│=│y2-y1│两点间的距离公式:例如:平面内A(2, 1),B(3,5),则二、两角和的余弦公式的推导 xyoP1P2αβP4P3-β(1,0)(cosα,sinα)(cos(α+β),sin(α+β))(cos(-β),sin(-β))观察:图中还有哪些相等关系?二、两角和的余弦公式的推导xyoP1P2二、两角和的余弦公式的推导xyoP1P2xyoP1P2二、两角和的余弦公式的推导二、两角和的余弦公式的推导xoP1P2αβP4P3-β(1,0)(cosα,sinα)(cos(α+β),sin(α+β))(cos(-β),sin(-β))y由两点间的距离公式可得:P1P3 =P2P4 由 P1P3= P2P4,得 展开并整理得: 即: 即:两角和的余弦公式为:
两角差的余弦公式的推导:在公式中用-β代替,就得到
即:两角差的余弦公式为:
这个公式对任意的角都成立。 例 题:例1:求三角函数 COS75°的值 课堂练习: 1. 求下列三角函数的值练习答案:课堂小结: 1. 平面内两点间的距离公式: 若P1(x1,y1), P2 (x2,y2),则 2. 两角和与差的余弦公式: 3. 以上两公式的推导及应用。 课后作业: 1. 课本P40 习题4.6 3. (3) (4) (6) (8) 2. 预习内容:P35-36
一、平面内两点间距离公式的引入 x.P1(x1,y1)yo.P2(x2,y2)M1M2N1N2(0,y1)(0,y2)Q P1Q = M1M2QP2 = N1N2由勾股定理得: 由此可得平面内P1(x1,y1), P2(x2,y2)(x1,0)(x2,0)
想一想,数轴上两点间的距离是如何求得的?ABOxx1x2 AB=│x2-x1│=│x2-x1│=│y2-y1│两点间的距离公式:例如:平面内A(2, 1),B(3,5),则二、两角和的余弦公式的推导 xyoP1P2αβP4P3-β(1,0)(cosα,sinα)(cos(α+β),sin(α+β))(cos(-β),sin(-β))观察:图中还有哪些相等关系?二、两角和的余弦公式的推导xyoP1P2二、两角和的余弦公式的推导xyoP1P2xyoP1P2二、两角和的余弦公式的推导二、两角和的余弦公式的推导xoP1P2αβP4P3-β(1,0)(cosα,sinα)(cos(α+β),sin(α+β))(cos(-β),sin(-β))y由两点间的距离公式可得:P1P3 =P2P4 由 P1P3= P2P4,得 展开并整理得: 即: 即:两角和的余弦公式为:
两角差的余弦公式的推导:在公式中用-β代替,就得到
即:两角差的余弦公式为:
这个公式对任意的角都成立。 例 题:例1:求三角函数 COS75°的值 课堂练习: 1. 求下列三角函数的值练习答案:课堂小结: 1. 平面内两点间的距离公式: 若P1(x1,y1), P2 (x2,y2),则 2. 两角和与差的余弦公式: 3. 以上两公式的推导及应用。 课后作业: 1. 课本P40 习题4.6 3. (3) (4) (6) (8) 2. 预习内容:P35-36
