2022秋季班九年级数学人教版辅导课件(能力提高班)第5讲 二次函数与方程不等式 课件(共82张PPT)
文档属性
| 名称 | 2022秋季班九年级数学人教版辅导课件(能力提高班)第5讲 二次函数与方程不等式 课件(共82张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 54.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-29 22:12:51 | ||
图片预览






文档简介
(共82张PPT)
wkwuwwwkwuwwwuwwwwwwku
讲次:
二次函数与方程
不等式
wbwwwwwwwwwwwkw
模块:
二次函数与方
程、不等式
wbwbwwwkwbwbbwbwwkwbwb
知识解读
AIXUEXI
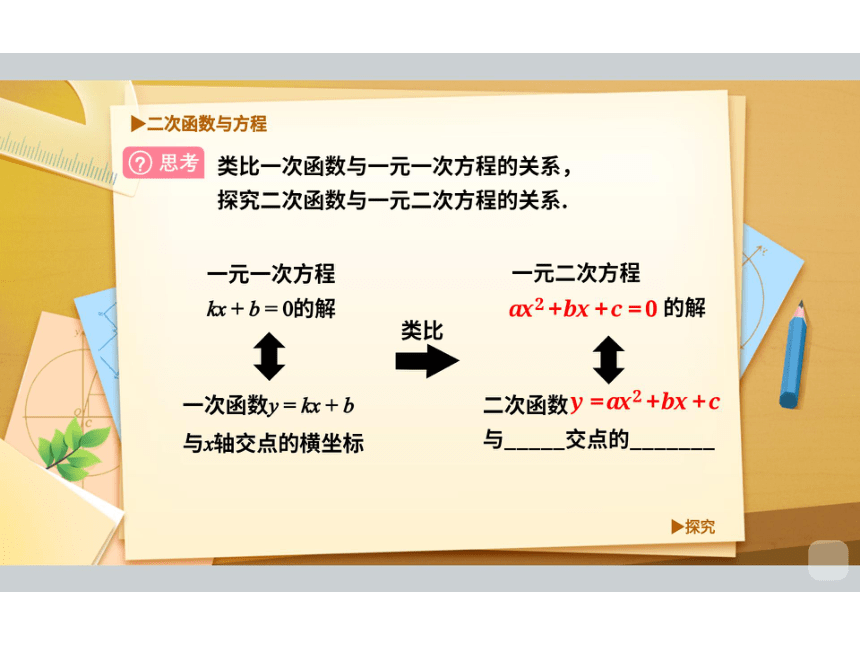
◆二次函数与方程
hbwbw
②思考
类比一次函数与一元一次方程的关系,
探究二次函数与一元二次方程的关系.
一元一次方程
一元二次方程
+b=0的解
x2+bX+c=0的解
类比
一次函数y=+b
二次函数y=x2+bx+C
与x轴交点的横坐标
与交点的
探究
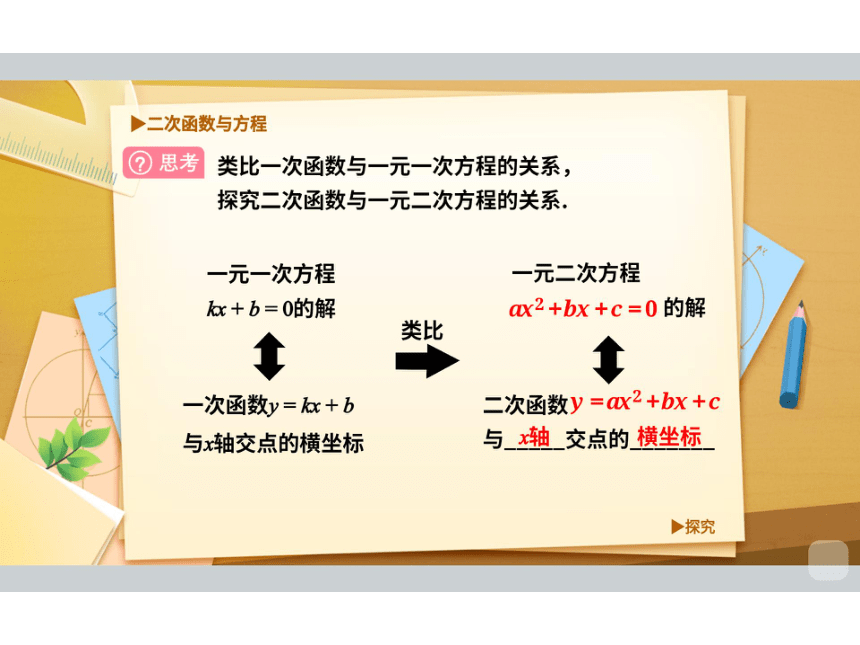
◆二次函数与方程
hwbwkwkuwkw
②思考
类比一次函数与一元一次方程的关系,
探究二次函数与一元二次方程的关系.
一元一次方程
一元二次方程
+b=0的解
x2+bX+c=0的解
类比
一次函数y=+b
二次函数y=x2+bx+C
与x轴交点的横坐标
与轴交点的横坐标
探究
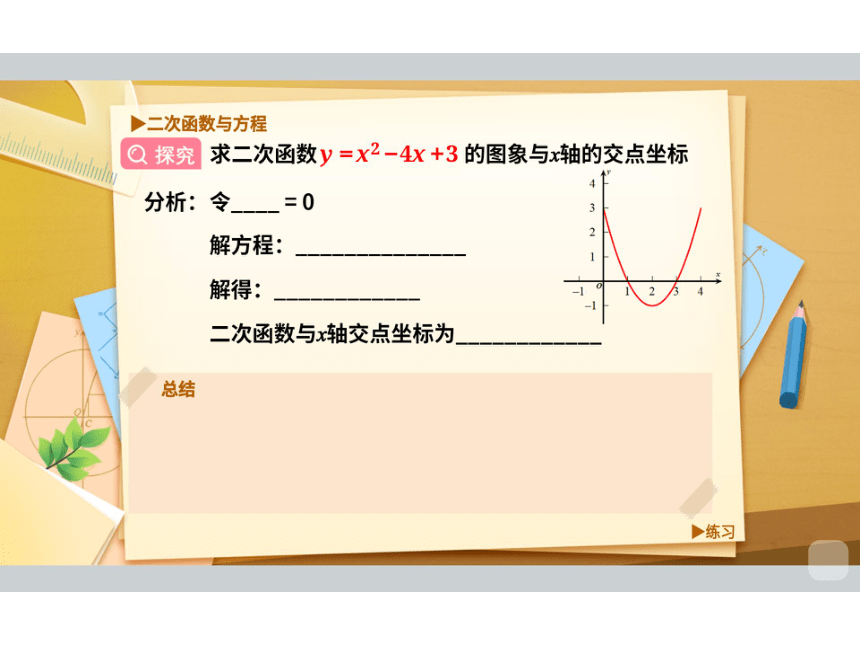
◆二次函数与方程
bbkk
探究
求二次函数y=X2-4X+3的图象与x轴的交点坐标
4
分析:令=0
3
2
解方程:
A
解得:
二次函数与x轴交点坐标为
总结
>练习
◆二次函数与方程
Q探究
求二次函数y=X2-4X+3的图象与x轴的交点坐标
4
分析:令y=0
3
解方程:x2-4X+3=0
解得:X1=1X2=3
二次函数与x轴交点坐标为(1,0)和(3,0)
总结
二次函数y=x2+bX+C与x轴交点的横坐标
等于对应的一元二次方程x2+bX+C=0的解,
求二次函数与x轴交点坐标的步骤:
①令y=0②解一元二次方程③写交点坐标
D练习
◆二次函数与方程
hbbwkww
上练习
1、已知抛物线y=x2+bX+C与x轴的交点
分别是A(-1,0)、B(5,0),则一元二次方程
X2+bX+C=0的根是
2、已知方程x2+bx+c=0(a≠0)的解是
X1=5,X2=-3,那么抛物线y=X2+bx+c
与x轴的两个交点坐标分别是
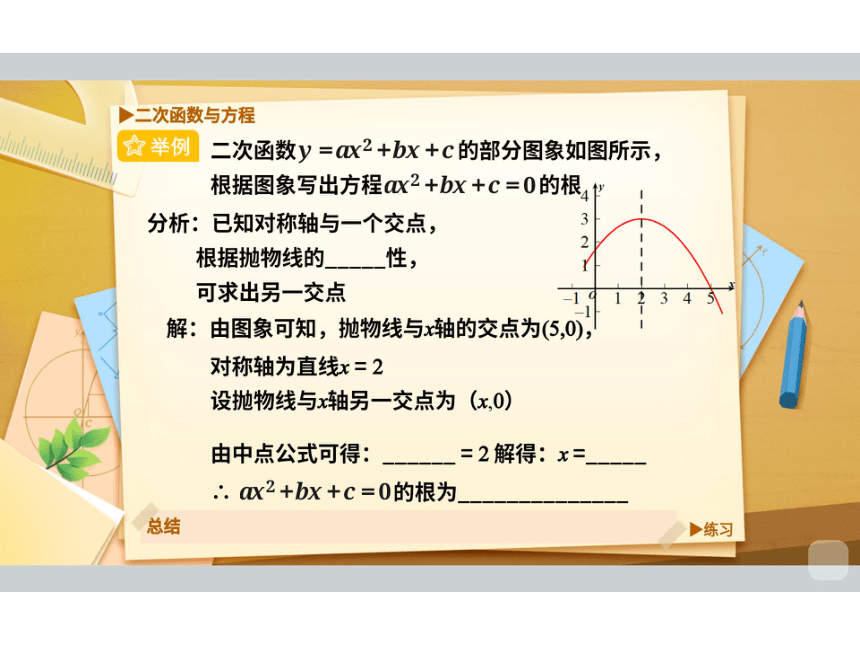
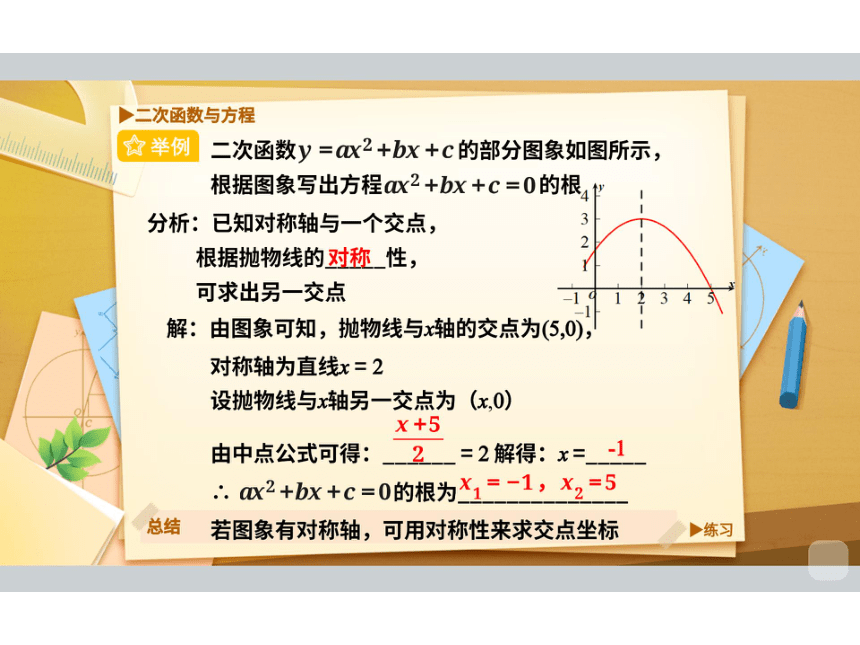
举例
二次函数与方程
hbbwkww
上练习
1、已知抛物线y=ax2+bx+C与x轴的交点
分别是A(-1,0)、B(5,0),则一元二次方程
x2+bX+C=0的根是X1=-1,X2=5
2、已知方程x2+bx+c=0(a≠0)的解是
X1=5,X2=-3,那么抛物线y=x2+bx+C
与x轴的两个交点坐标分别是(5,0)和(-3,0)
>举例
wkwuwwwkwuwwwuwwwwwwku
讲次:
二次函数与方程
不等式
wbwwwwwwwwwwwkw
模块:
二次函数与方
程、不等式
wbwbwwwkwbwbbwbwwkwbwb
知识解读
AIXUEXI
◆二次函数与方程
hbwbw
②思考
类比一次函数与一元一次方程的关系,
探究二次函数与一元二次方程的关系.
一元一次方程
一元二次方程
+b=0的解
x2+bX+c=0的解
类比
一次函数y=+b
二次函数y=x2+bx+C
与x轴交点的横坐标
与交点的
探究
◆二次函数与方程
hwbwkwkuwkw
②思考
类比一次函数与一元一次方程的关系,
探究二次函数与一元二次方程的关系.
一元一次方程
一元二次方程
+b=0的解
x2+bX+c=0的解
类比
一次函数y=+b
二次函数y=x2+bx+C
与x轴交点的横坐标
与轴交点的横坐标
探究
◆二次函数与方程
bbkk
探究
求二次函数y=X2-4X+3的图象与x轴的交点坐标
4
分析:令=0
3
2
解方程:
A
解得:
二次函数与x轴交点坐标为
总结
>练习
◆二次函数与方程
Q探究
求二次函数y=X2-4X+3的图象与x轴的交点坐标
4
分析:令y=0
3
解方程:x2-4X+3=0
解得:X1=1X2=3
二次函数与x轴交点坐标为(1,0)和(3,0)
总结
二次函数y=x2+bX+C与x轴交点的横坐标
等于对应的一元二次方程x2+bX+C=0的解,
求二次函数与x轴交点坐标的步骤:
①令y=0②解一元二次方程③写交点坐标
D练习
◆二次函数与方程
hbbwkww
上练习
1、已知抛物线y=x2+bX+C与x轴的交点
分别是A(-1,0)、B(5,0),则一元二次方程
X2+bX+C=0的根是
2、已知方程x2+bx+c=0(a≠0)的解是
X1=5,X2=-3,那么抛物线y=X2+bx+c
与x轴的两个交点坐标分别是
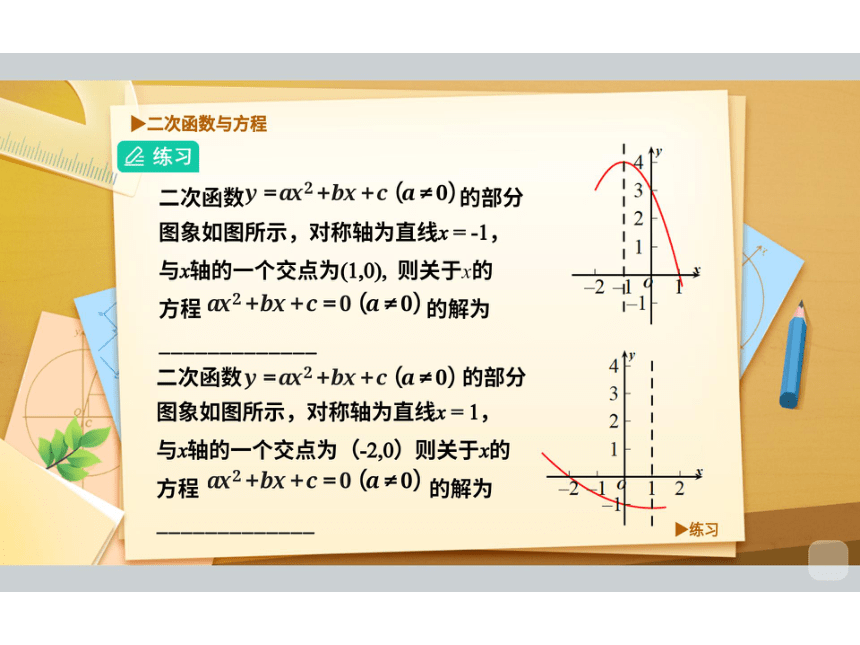
举例
二次函数与方程
hbbwkww
上练习
1、已知抛物线y=ax2+bx+C与x轴的交点
分别是A(-1,0)、B(5,0),则一元二次方程
x2+bX+C=0的根是X1=-1,X2=5
2、已知方程x2+bx+c=0(a≠0)的解是
X1=5,X2=-3,那么抛物线y=x2+bx+C
与x轴的两个交点坐标分别是(5,0)和(-3,0)
>举例
同课章节目录
