总复习 分数乘法(课件)六年级上册数学人教版(共118张PPT)
文档属性
| 名称 | 总复习 分数乘法(课件)六年级上册数学人教版(共118张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 561.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-30 06:08:35 | ||
图片预览










文档简介
(共118张PPT)
分数乘法
分 数 乘 法
分数乘整数
分数乘分数
小数乘分数
整数运算定律推广到分数乘法
分数乘法应用题
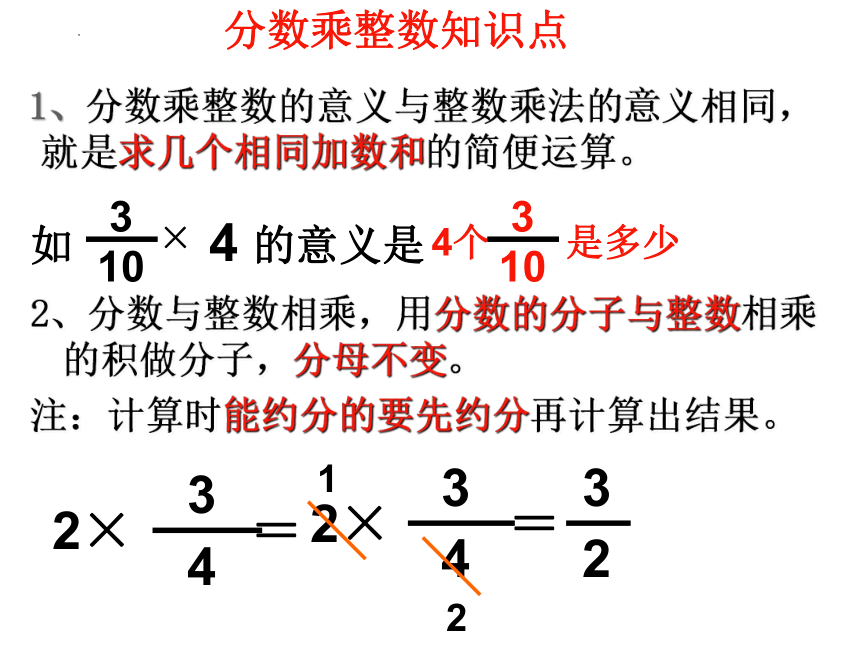
分数乘整数知识点
1、分数乘整数的意义与整数乘法的意义相同,就是求几个相同加数和的简便运算。
2、分数与整数相乘,用分数的分子与整数相乘的积做分子,分母不变。
注:计算时能约分的要先约分再计算出结果。
4
3
2× =
4
3
2× =
2
1
2
3
×
10
3
4
如 的意义是
4个 是多少
10
3
分数乘整数知识点:强调
1、一个整数乘分数有时表示几个相同的分数相加,有时表示这个整数的几分之几
×
10
3
4
如 的意义可以是
也可以是 只有有具体情境时才能分到底是几个相同加数的和还是这个数的几分之几。
4个 是多少
10
3
4的 是多少
10
3
分数乘整数知识点:强调
如第2页课本例1,就只能是3个 相加是多少?
4
1
所以配套练习册19页的我会判断的第一小题
9
2
×
9
1
5
计算方法相同,意义也是
5× 和
9
1
相同的这句话是正确的。
而第3页的例2的第3小题则只能是求12的 是多少?
1、整数乘法的意义:(
)
求几个相同加数和
的简便运算
2、同分母分数相加减只把( )相加减( )不变,计算结果( )
分子
分母
能约分的要约成最简分数
分数乘整数练习
3、分数乘整数的意义与( )的意义相同,就是求( )的( )。
求几个相同加数和
整数乘法
简便运算。
4、分数乘整数的计算法则
①分数与整数相乘,用( )做分子,( )不变。
②计算时( )再计算出结果。
分数的分子与整数相乘的积
分母
能约分的要先约分
5、分数乘整数,用( )作分子,( )不变。
分数的分子与整数相乘的积
分母
9
7
+
9
7
+
9
7
=( )×( )=( )
2
1
+
2
1
=( )×( )=( )
9
7
3
3
7
2
1
2
3
1
1
6、
1
1
8
7
+
8
7
+
8
7
=( )×( )=( )
8
7
3
8
21
×
10
3
4
7、 的意义是( )
4个 是多少
10
3
×
8
7
6
的意义是( )
4的 是多少
10
3
6个 是多少
8
7
6的 是多少
8
7
平方米=( )平方分米
时=( )分
( )与整数乘法的意义相同。
1、
2、
分数乘整数的意义
1平方米=100平方分米
由平方米到平方分米是由高级单位到低级单位,要乘它们的进率100,
25
8
×
100
25
8×100
=
=32
1
4
32
1时=60分
由时到分是由高级单位到低级单位,要乘它们的进率60,
4
3
×
60
4
3×60
=
=45
1
15
45
一根绳子长
米,3根这样的绳子共长( )米;这根
长( )米。
绳子的
3、
3根共长多少就是求3个 是多少
10
9
×
3
10
9×3
=
=
10
27
(米)
这根绳子的 长多少米,就是求 的 是多少。
10
9
×
10×3
9×1
=
=
10
3
(米)
3
1
1
3
10
27
10
3
比30多 的数是( )比35的 多3的数是( )。
4、
7
2
×
35
7
35×2
=
=
13
6
1
7
2
比30多 ,这里没有说是30的 ,所以这里的两个数都是确定的数值,可以直接相加。
6
1
6
1
30
6
1
比35的 多3,这里的 是30的 ,在这里是一个比率不是一个确定的值。所以列式为
7
2
7
2
7
2
+3
+3
1
5
13
8
3
×
3
4
×
4
3
8
3
×
8
5
×
6
5
8、计算
8
3×3
=
8
9
=
8
3×8
=
=3
1
1
4
4×3
=
=3
1
1
6
5×5
=
6
25
=
9、计算
3
4
3
2
10
3
3× =
10
3×3
=
10
9
4
3
2× =
4
2×3
=
2
3
2
1
4
3
2× =
4
3
2× =
2
1
2
3
1
0
7
2
×
14
2
= ×
7
16
14
1
=
1
16
2
= 32
2
×
7
2
2
=
7
2×7+2
=
7
16
带分数乘一个数,要先把带分数化成假分数后再按分数乘法的计算方法进行计算。
8
3
×
8
1
= ×
8
11
8
1
=
1
11
1
= 11
1
×
8
3
1
=
8
1×8+3
=
8
11
带分数乘一个数,要先把带分数化成假分数后再按分数乘法的计算方法进行计算。
10、列式计算
(1)3个 相加是多少?
8
3
8
3
×3=
8
3×3
=
8
9
(2) 的15倍是多少?
5
2
5
2
×15=
5
2×15
=
1
6
1
3
=6
(3)3 的 是多少?
8
3
3× =
8
3×3
=
8
9
(4)15的 是多少?
5
2
5
2
15× =
5
15×2
=
1
6
1
3
=6
8
3
一张报纸的厚度大约是 mm 。100张这样的报纸叠放在一起厚度大约是多少厘米。
5
2
任何解决问题都应先看单位名称是否相同,如不相同一定要换算单位。
100
× =
5
2
100
×
5
2
20
1
(mm)
=4(厘米)
答:略
=40
解决问题
分数乘分数的知识点
1、分数乘分数的意义就是求这个数的几分之几是多少。
注:求一个数的几倍或是求这个数的几分之几都要用乘法,也就是说问题中的“的”字要换成乘号。
如12的 是多少?
3
1
列式为12×
3
1
如12的3 倍是多少?
列式为12×3
× 的意义是( )
5
1
2
1
的 是多少
5
1
2
1
1、一个数乘分数的意义就是( )
求这个数的几分之几是多少
10
3
3×
3、 的意义是( )
3的 是多少
10
3
分数乘分数的练习
2、分数与分数相乘,用( )做分子,( )做分母。
分子与分子相乘的积
分母与分母相乘的积
9
1
×
的意义是( )
的 是多少
9
1
9
5
9
5
4、路程=( )
速度×时间
3个 是多少
10
3
5、从 吨水泥中运走 ,还剩下( )吨;从 吨水
泥中运走 吨,还剩下( )吨。
4
3
5
2
4
3
5
2
从 吨中运走 ,这里是 吨的 ,是把水泥
的总数量看做单位“1”,平均分成5份,运走了其中的两份,所以还剩下其中的3份。可以列式为:
4
3
5
2
4
3
5
2
4
3
-
4
3
=
×
5
2
4
3
=
×
5
3
20
9
(吨)
20
9
从 吨水泥中运走 ,还剩下( )吨;从 吨水泥中
运走 吨,还剩下( )吨。
4
3
5
2
4
3
5
2
从 吨中运走 吨,这里运走的是 吨,是一个
确定的数值,求还剩下多少吨,就用数量关系式:
总数-运走的=剩下的
4
3
5
2
5
2
4
3
-
=
5
2
20
15
=
-
20
8
20
7
(吨)
20
7
20
9
6、李伯伯家有一块 公顷的地。种土豆的
面积占这块地的 ,种土豆的面积是多少
公顷?
2
1
这里是把( )看做单位“1”,是( )
要求( ),也就是求
( )
列式计算( )
5
1
这块地的面积
2
1
公顷
种土豆的面积是多少公顷
的 是多少
5
1
2
1
× = ( 公顷 )
5
1
2
1
10
1
×2 ○
8×
○8
×
○
×
○
×
×1 ○
2
1
×
8
1
( + )
5
1
2
1
×
8
1
+
5
1
○
2
1
9、
一个数乘一个大于1的数所得的积大于它本身
>
一个数乘一个小于1的数所得的积小于它本身
<
一个数乘一个小于1的数所得的积小于它本身
<
>
一个数乘1的数所得的积等于它本身
=
2
1
×
8
1
+
2
1
×
8
1
<
( + )
5
1
2
1
×
8
1
+
5
1
○
5
1
×
8
1
○
<
2
1
8
3
×
3
4
×
4
3
3
2
×
3
2
5
2
×
5
2
8
3
×
8
5
×
6
5
3
2
+
3
2
5
2
+
5
2
6、计算
8
3×3
=
8
9
=
8
3×8
=
=3
1
1
4
4×3
=
=3
1
1
6
5×5
=
6
25
=
3×3
2×2
=
9
4
=
3
2+2
=
3
4
=
5×5
2×2
=
25
4
=
5
2+2
=
5
4
=
7
2
×
2
= ×
7
16
1
=
7×1
2
5
=
2
×
带分数乘一个数,要先把带分数化成假分数后再按分数乘法的计算方法进行计算。
8
5
8
5
7
10
8
3
×
2
1
= ×
8
11
1
=
1×3
11
1
1
×
带分数乘一个数,要先把带分数化成假分数后再按分数乘法的计算方法进行计算。
3
2
3
8
=
3
11
8、列式计算
(1) 公顷 的 是多少?
12
5
12
5
× =
12×7
5×4
=
21
5
(2) dm的 是多少分米?
3
2
1
3
(公顷)
7
4
7
4
5
4
3
2
× =
5
4
3
2
× =
5
4
15
8
(分米)
一个长方形的长是 m 。宽是长的 。
这个长方形的面积是多少平方米。
6
5
长方形的面积=长×宽。
宽:
×
6
5
×
6
5
2
1
=
答:略
10
9
这里知道长,但不知道宽要先求宽
10
9
=
10
9
2
3
4
3
面积:
×
10
9
4
3
=
10×4
9×3
=
40
27
(米)
(米 )
解决问题
每千克小麦可磨成面粉 kg。 t 小麦
或磨成面粉多少千克?
2
3
×1000
×1000
1
500
=1500
答:略
5
4
2
3
=
2
3
换算单位:
×1500
5
4
=
5
4
=1200
(千克)
(千克)
任何解决问题都应先看单位名称是否相同,如不相同一定要换算单位。
×1500
1
300
修一条长6km的道路,第一期完成了这
条路的 ,第二期完成了这条路的 。第一期比第二期多修了多少千米?
10
3
5
2
任何解决问题第一步都应先看单位名称是否相同,如不相同一定要换算单位。这里不需要换算。
第二步就是找重要的数学信息,或者说是解题关键。
修一条长6km的道路,第一期完成了这
条路的 ,第二期完成了这条路的 。第一期比第二期多修了多少千米?
10
3
5
2
得出第一个数量关系式第一期完成的等于这条路
总长的 可以表示为(一)=总长×
5
2
5
2
得出第二个数量关系式第二期完成的等于这条路
总长的 可以表示为(二)=总长×
10
3
10
3
修一条长6km的道路,第一期完成了这
条路的 ,第二期完成了这条路的 。第一期比第二期多修了多少千米?
10
3
5
2
最后是看问题,让我们求什么?
这里是让我们求第一期比第二期多修了多少千米?
同样存在一个数量关系式,第一期比第二期长的千米数等于第一期的减第二期的可表示为:
(一)比(二)多的=(一)-(二)
修一条长6km的道路,第一期完成了这
条路的 ,第二期完成了这条路的 。第一期比第二期多修了多少千米?
10
3
5
2
总长×
5
2
总长×
10
3
(一)比(二)多的=(一)-(二)
=
=
由此我们可以列式为:
6×
5
2
-
6×
10
3
=
6×
10
1
3
5
=
5
3
(千米)
答:略
小数乘分数的知识点
1、小数乘分数的意义就是求这个数的几分之几是多少。
1.2× 的意义是( )
5
1
1.2的 是多少
5
1
2、计算小数乘分数时,可以把小数转化成分数进行计算;在计算小数乘分数时,如果小数能和分数的分母约分,可以先约分再计算,这样可以使计算简便。
如:
7
2
×
2.8
7
2
×
2.8
= ×
2.8=
7
2
10
28
5
14
5
14
=
5
14
1
2
= ×
1
2
5
2
=
5
4
7
2
2.8
= ×
7
2
1
0.4
= ×
1
2
= 0.8
×
2.8
0.4
72
17
×
17
16
21
20
×0.42
44
25
×1.1
4
1
0.32×
7
5
×5.6
12
7
×0.36
17
3
×5.1
计算
72
17
×
17
16
=
72
17
×
17
16
=
1
1
9
2
9
2
21
20
×0.42
=
21
20
×0.42
=0.4
1
0.02
44
25
×1.1
=
44
25
×1.1
=
4
0.1
4
2.5
=
8
5
4
1
0.32×
=
4
1
0.32×
=0.08
1
0.08
7
5
×5.6
=
7
5
×5.6
=4
1
0.8
12
7
×0.36
=
12
7
×0.36
=
1
0.03
17
3
×5.1
=
17
3
0.21
=0.9
1
0.3
×5.1
1、每千克花生可榨油0.38千克。 吨花生米可榨油多
少千克?
4
5
这里单位不同应换算成相同的单位后再进行了计算
4
5
1吨=1000千克,由大单位到小单位要乘它们的进率
×1000=
4
5
×1000=
1
250
1250千克
1250×0.38=
475
答:略
(千克)
解决问题
2、码头有125.5吨货物,上午运走总数的 ,下午
运走的是上午的 ,下午运走总数的几分之几?下午运走多少吨?
5
2
4
3
上午运走总数的 ,是把总数看做单位“1”,平均分
成5份,上午运走了这样的2份。
5
2
下午运走的是上午的 ,是把上午运走的数量看做
单位“1”,平均分成4份,下午运走了这样的3份。
4
3
下午运走的是上午的 也就是 的
4
3
5
2
4
3
上午运走的
125.5吨
下午运走的=
总数
上午运走的
=总数×
5
2
上午运走的数量
4
3
=
总数×
5
2
×
=
1
(1)下午运走总数的几分之几?
=
4
3
5
2
×
=
4
3
5
2
×
1
2
10
3
(2)下午运走了多少吨?
10
3
125.5×
=
10
3
125.5×
=37.65(吨)
1
12.55
答:略
答:略
2
1
找规律
3
1
9
2
, , ,( ),( )
3
1
÷
=
2
1
3
1
=
× 2
3
2
9
2
÷
=
3
1
9
2
=
× 3
3
2
3
1
×
3
2
×
3
2
×
3
2
27
4
×
3
2
81
8
整数运算定律推广到分数乘法
1、分数乘加、乘减混合运算与整数混合运算顺序相同。
(1)、如果只有乘除或只有加减,按从左往右的顺序依次进行计算
(2)、如果既有乘除又有加减,要先算乘除再算加减
(3)、有括号的要先算括号里面的。
5 -
6
1
×( )
3
2
这里运用乘法分配律也不简便,所以就按照有括号的要先算括号里面的来进行运算。
=
2
6
1
×( - )
15
3
3
整数化成分数,用整数乘分母的积做分子。
=
×
6
1
=
18
13
3
13
×5
2
1
×
2
1
同一级运算按从左往右的顺序依次进行计算。
=
×5
2
1
×
1
×
2
用不到的数字及符号要落下来。
=
×5
4
1
=
4
5
2
1
+
2
1
×5
既有乘除又有加减,要先算乘除再算加减。
=
2
5
用不到的数字及符号要落下来。
=
2
1
=
2
1+5
2
1
+
1
×5
2
+
=3
同分母分数相加,只把分子相加,分母不变。
8
3
+
8
7
×7
既有乘除又有加减,要先算乘除再算加减。
=
8
3
用不到的数字及符号要落下来。
=
8
49
=
8
52
8
3
+
7
×7
8
+
=
同分母分数相加,只把分子相加,分母不变。
13
2
13
2
能约分的一定要约成最简分数。
3
2
+
3
1
×
既有乘除又有加减,要先算乘除再算加减。
=
5
1
用不到的数字及符号要落下来。
=
3
2
=
15
10
3
2
+
1
×3
3×5
+
=
异分母分数相加,先把它们通分成同分母分数,再按同分母分数的方法进行计算。
5
3
+
15
3
15
13
1
1
整数运算定律推广到分数乘法
2、整数乘法的运算定律对于分数乘法同样适用。
(1)、乘法交换律:交换两个因数的位置积不变。用字母表示:a×b=b×a
2
1
×
8
1
2
1
×
8
1
○
=
2
1
×
100
19
×
8
5
=
100
19
×
×
=
2×1×8
19×1×5
=
16
95
50
8
5
1
50
1
2
×
100
19
×
8
5
=
100
19
×
×
=
2×8×1
19×1×5
=
16
95
50
8
5
1
50
5
2
20
1
整数运算定律推广到分数乘法
2、整数乘法的运算定律对于分数乘法同样适用。
(a×b)×c=a×(b×c)
2
7
×
3
5
3
5
×
2
7
○
=
7
3
(2)、乘法结合律:先把前两个相乘再与第三个数相乘或先把后两个数相乘再与第一个数相乘,积不变:用字母表示为:
( )
×
7
3
×
( )
×
9
14
×
23
7
=
9
14
×
×1
×
=
23
7
=
23
7
14
9
14
9
23
7
1
1
1
1
×
9
14
×
23
7
=
9
14
×
1×
×
=
23
7
=
23
7
14
9
14
9
23
7
1
1
1
1
整数运算定律推广到分数乘法
2、整数乘法的运算定律对于分数乘法同样适用。
(3)、乘法分配律:两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加,积不变。
(a+b)×c=a×c+b×c
○
=
×
8
1
2
1
+
1
5
( )
2
1
+
1
5
×
8
1
8
1
×
87×
86
3
要用简便算法,那就要尽量约去分母,分母是86,就想办法让87变成86。87=86+1
=(86+1)×
86
3
=86× 1×
86
3
=
86
3+
3
86
+
=3
利用乘法分配律
用简便算法
1
1
3
86
3
整数与分数相加,直接组合在一起就行。
4.8×
6
1
12
( )
-
1
43×
42
5
16
3
-
8
7
×
8
7
99
×
5
2
+
5
2
101
×
10
7
-
10
7
乘法分配律专题训练
75×
+0.75×26
4
3
4
3
-
×
9
5
+
3
1
3
1
9
4
×
17×
8
3
47×
48
43
11
×
12
11
+
12
11
× 12
4
2
3
1
( )
-
101×
5
4
4.8×
6
1
12
1
=
1
5
24
×( - )
1
12
6
=
×
5
24
= -
5
4
6
1
( )
-
4.8=
48
24
5
24
=
10
5
×
5
24
12
1
-
4
1
48是6的倍数,也是12的倍数,所以这个题可以用乘法分配律来计算。
2
1
5
2
=
5
2
4.8×
6
1
12
1
=
×
4.8
= 0.8 - 0.4
6
1
( )
-
×
4.8
12
1
-
0.8
1
48是6的倍数,也是12的倍数,所以这个题可以用乘法分配律来计算。
0.4
1
= 0.4
43×
42
5
=
5
( 42 + 1)×
42
=
×
42
= +
5
42
5
×
1
42
5
+
1
1
整数43比分母42多1,我们可以把它写成42+1的形式。
42
5
=
42
5
5
16
3
-
8
7
×
=
8
7
=(1- )
16
3
=
16
13
16
3
-
7
1×
8
×
=
91
128
8
7
7
×
8
×
8
7
17×
8
3
=
3
( 16 + 1)×
8
=
×
16
= +
6
8
3
×
1
8
3
+
2
1
整数17比分母的2倍多1,我们可以把它写成16+1的形式。
8
3
=
8
3
6
99
×
5
2
+
=
5
2
=(99+1 )
=
100
5
2
+
2
×99
5
×
=
40
5
2
1
×
×
5
2
20
1
101
×
10
7
-
10
7
= (101 - 1 )
=
100
×
=
70
10
7
×
10
7
10
1
×1
11
×
12
11
+
=
12
11
=(11+1 )
=
12
12
11
+
11
×11
12
×
=
11
12
11
1
×
×
12
11
1
1
× 12
4
2
3
1
=
×
3
2
= 8 - 3
12
( )
-
×
4
1
12
-
4
1
3
1
= 5
101×
5
4
=
4
( 100 + 1)×
5
=
×
100
= +
80
5
4
×
1
5
4
+
20
1
5
4
=
5
4
80
47×
48
43
=
43
( 48 - 1)×
48
=
×
48
= -
43
48
43
×
1
48
43
-
1
1
48
43
=
48
5
42
×
9
5
+
3
1
=( + )
=
1
×
=
3
1
×
3
1
3
1
9
4
×
9
5
9
4
3
1
75×
+0.75×26
4
3
=( 75 + 26 - 1 )
=
100
×
=
4
3
×
4
3
4
3
-
75
=
75×
+ ×26
4
3
4
3
-
1×
4
3
25
1
39
25
×
30
13
=
39
25
×
30
13
=
5
6
3
1
18
5
11
6
×10
=
11
6
×10
=
3
2
×
15
7
15
7
2
×
1
11
28
100
19
×50
=
100
19
×50
=
2
1
×
8
3
8
3
×
16
57
9
7
-
=
27
14
=
×
3
2
7
2
-
7
2
=
189
98
189
54
-
189
44
计算出错较多的题
×
2
1
○
6
5
2
1
一个数乘小于1的数所得的积一定小于它本身。
<
×
5
○
3
1
3
1
<
×5
×
6
8
7
○
>
×
6
7
8
1
○
<
×
8
1
2
1
+
1
5
( )
2
1
+
1
5
×
8
1
5
3
3
5
一个数乘大于1的数所得的积一定大于它本身。
2
1
×
8
1
+
2
1
×
8
1
<
( + )
5
1
2
1
×
8
1
+
5
1
○
5
1
×
8
1
○
<
2
1
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
(1)两周一共卖出总数的几分之几?
(2)两周一共卖出多少双?
(3)还剩多少双?
5
1
8
3
任何解决问题第一步都应先看单位名称是否相同,如不相同一定要换算单位。这里不需要换算。
第二步就是找重要的数学信息,或者说是解题关键。
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
5
1
8
3
得出第一个数量关系式第一周卖出的的等于
总数的 可以表示为(一)=总数×
5
1
5
1
得出第二个数量关系式第二周卖出的等于
总数的 可以表示为(二)=总数×
8
3
8
3
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
(1)两周一共卖出总数的几分之几?
(2)两周一共卖出多少双?
(3)还剩多少双?
5
1
8
3
最后是看问题,让我们求什么?三个问题一个一个的解决。
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
(1)两周一共卖出总数的几分之几?
5
1
8
3
同样存在一个数量关系式,第一周的加第二周的就是两周一共卖出的。
两周一共卖出的=(一)+(二)
总数×
5
1
总数×
8
3
=
=
这里问的是卖出总数的几分之几,所以把总数看作单位“1”进行计算。
1×
1×
+
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
(1)两周一共卖出总数的几分之几?
5
1
8
3
5
1
8
3
=
+
40
8
40
15
=
+
40
23
答:略
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
(2)两周一共卖出多少双?
5
1
8
3
同样存在一个数量关系式,第一周的加第二周的就是两周一共卖出的。
两周一共卖出的=(一)+(二)
总数×
5
1
8
3
=
=
总数×
+
这里是求确定的数值,可列式为:
600×
5
1
+
600×
8
3
=
600×
40
23
15
1
=
345(双)
答:略
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
(3)还剩多少双?
5
1
8
3
同样存在一个数量关系式,总数减去卖出的等于剩下的剩下的=总数 - 卖出的
600
-
345
=
225(双)
答:略
图书室新进一批图书,其中故事书占总数
的 ,科技书的本数是故事书的 ,文
艺书的本数是科技书的 。文艺书的本数占总数的几分之几 。
20
3
5
3
9
2
任何解决问题第一步都应先看单位名称是否相同,如不相同一定要换算单位。这里不需要换算。
第二步就是找重要的数学信息,或者说是解题关键。
图书室新进一批图书,其中故事书占总数
的 ,科技书的本数是故事书的 ,文
艺书的本数是科技书的 。文艺书的本数占总数的几分之几 。
20
3
5
3
9
2
故事书的本数=总数×
20
3
科技书的本数=故事书的本数×
5
3
文艺书的本数=科技书的本数×
9
2
故事书的本数=总数×
20
3
科技书的本数=故事书的本数×
5
3
文艺书的本数= 科技书的本数 ×
9
2
最后让我们求科技书的本数占总数的几分之几?
我们可以依次替代
总数×
20
3
总数×
20
3
×
5
3
最后仅是让我们求占总数的几分之几,不是确定的数值,所以把总数看作单位“1”
1
9
2
×
20
3
×
5
3
=
9
2
×
20
3
×
5
3
=
10
1
1
3
50
1
1
1
答:略
学校将300本图书分给六年级的三个班,六(1)班分到
六(2)班分到 ,剩下的分给六(3)班。六(3)班
分到多少本图书?
4
1
5
2
六(2)=总数×
4
1
这里说六(二)班分到 ,没说是说的,就是
顺着来的,也就是也是总数的 ,列式为
5
2
5
2
六(1)=总数×
5
2
六(3)=总数 - 六(1)-六(2)
300 - 300× -300×
4
1
5
2
学校将300本图书分给六年级的三个班,六(1)班分到
六(2)班分到 ,剩下的分给六(3)班。六(3)班
分到多少本图书?
4
1
5
2
300 - 300× -300×
4
1
5
2
=300 - 75 - 120
=105(本)
300 ×(1- - )
4
1
5
2
=300 ×
20
7
=105(本)
答:略
分数乘法应用题
做任何应用题都是按以下三步去做:
(1)、审题:认真读题,看单位是否需要换算。找重要的数学信息。
(2)、分析:对找到的数学信息进行分析,写出相应的数量关系式。
(3)、解题:看问题让我们求的是什么,找能解答问题的数量关系式进而解题。
注:本单元重点教我们找单位“1”,谁的几分之几谁就是单位“1”;或者是和谁比较谁就是标准,就要把它平均分,那么它就是单位“1”
(4)、检查、验算。
梨树棵数的 与苹果树同样多,是把( )
看作单位“1”。如果梨树有28棵,那么苹果树有( )棵。
7
3
谁的 ,谁就是单位“1”,这里说的是梨树棵数的
所以这里是把梨树的棵数看作单位“1”。
梨树的棵数
知道梨树的棵树,求苹果树的棵数,还是要用到上面那句话
28×
7
3
7
3
7
3
×
=
的棵数
=
28×
7
3
=
1
4
12
(棵)
12
甲数比乙数多 ,是把甲数看作单位“1” ( )
5
1
补充完整是:甲数比乙数多的占乙数的 ,这里是把
乙数平均分成5份,甲比它多这样的1份,把乙平均分了,那么乙就是单位“1”所以这句话是错的。
5
1
×
甲数的 等于乙数的 ,则甲数小于乙数。 ( )
5
4
3
2
×
=
×
=1
=
4
5
=
2
3
4
6
<
=
这里这个题成立的先决条件是这两个数都不为零,但是它没有就所以这个题目是错的。如果说了它俩都不为零就是对的。
×
实际产量比原计划多 。这句话是指实际比原计划多的产量是
( ) 的
4
1
补充完整是:实际产量比原计划多的占原计划的 ,所以选B
4
1
4
1
A、实际产量 B、原计划产量 C、多的产量
B
6
5
×15
=
6
5
=
5
×15
2
2
25
1
1、甲数是乙数的 ,是把( )看作单位“1”
5
2、甲数的 是乙数,是把( )看作单位“1”
1
5
乙数
甲数
(1)、一块布用去 中单位“1”是( )
5
3
(2)、吃了一袋大米的 :( )
8
5
(3)、运走了一堆煤的 ( )
9
7
(4)、看了一本书的 :( )
6
5
这块布的总长
这袋大米的总重量
这堆煤的总重量
这本书的总页数
找单位“1”
一个大棚共480m ,其中一半种各种萝卜,
红萝卜地的面积占整块萝卜地的 ,红萝卜地有多少平方米 ?
4
1
整个大棚的面积是( )
2
1
480平方米
萝卜地的面积占整个大棚面积的( )
一半也就是
红萝卜地的面积占萝卜地面积的( )
4
1
要求的是( )面积
红萝卜地的
例8:
一个大棚共480m ,其中一半种各种萝卜,
红萝卜地的面积占整块萝卜地的 ,红萝卜地有多少平方米 ?
4
1
480平方米
各种萝卜地占大棚面积的
2
1
红萝卜地占萝卜地面积的
4
1
一个大棚共480m ,其中一半种各种萝卜,
红萝卜地的面积占整块萝卜地的 ,红萝卜地有多少平方米 ?
4
1
先求( )这里是把( )看作单位“1”,要求( ),也就是
求( ),列式为(
2
1
种萝卜的地的面积
480的 是多少
大棚的总面积
种萝卜的地的面积
2
1
480× =480× =240( m )
2
1
1
240
一个大棚共480m ,其中一半种各种萝卜,
红萝卜地的面积占整块萝卜地的 ,红萝卜地有多少平方米 ?
4
1
再求( )这里是把( )看作单位“1”,要求( ),也就是求
( ),列式为(
4
1
种红萝卜的地的面积
240的 是多少
种各种萝卜的地的面积
种红萝卜的地的面积
4
1
240× =240× =60( m )
4
1
1
60
一个大棚共480m ,其中一半种各种萝卜,
红萝卜地的面积占整块萝卜地的 ,红萝卜地有多少平方米 ?
4
1
4
1
480× ×
8
1
1
60
2
1
=480×
=60(m )
答:略
奶牛场每头奶牛平均日产牛奶 吨,42
头奶牛100天可产奶多少吨?
这里要先求( )这里是把
( )看做单位“1”,是( )
要求( ),也就是求
( )
列式计算( ) 再
求( ),
列式计算( )
42头牛一天产奶多少吨
50
1
吨
每头奶牛每天的产奶量
42个 是多少
50
1
50
1
42头牛一天产奶多少吨
×42= = (吨)
50
1
50
1×42
21
25
25
21
42头牛100产奶多少吨
×100= =84 (吨)
25
21
25
21×100
4
1
六一班有男生25人,比女生多2人,全班人数的 已达到《体
育锻炼标准》,达到《体育锻炼标准》的有多少人?
8
5
做解决问题先看单位,这里单位不需要换算。
找出解题的关键
这句话我们可以这样理解
全班总人数的 已达到《体育锻炼标准》
8
5
=
×
全班人数等于男生人数加女生人数
男生比女生多2人,就是女生比男生少2人所以应用25减2求女生人数
(25+25-2)
8
5
×
=
48
8
5
=
6
×
1
(人)
30
答:略
小军读一本315页的《哈利波特》第一天读了全书的 ,第二
天读了剩下的 ,第二天读了多少页?
7
2
做解决问题先看单位,这里单位不需要换算。
找出解题的关键
第一天读了全书的
8
5
=
×
问题是求第二天读了多少页,就用第二个数量关系式,只要知道剩下多少页就能求出,但题目中没有说剩下多少,我们只能用总数减去第一天看的求出剩下的再进行第二步的计算。
315×(1- )
5
1
×
=
315
7
5
=
45
×
1
(页)
45
答:略
5
1
第二天读了剩下的
5
1
=
×
7
2
5
1
×
1
1
一种电视机原价1200元,先涨价 ,再降价 。现在这
种电视机每台售价多少元?
10
1
做解决问题先看单位,这里单位不需要换算。
找出解题的关键
先涨的价是原价的
10
1
=
×
最后求现价,就是先在原价的基础上加上原价的
之后再在涨后的价格的基础上再除它的
10
1
再除的价是涨价后的
10
1
=
×
10
1
10
1
1200×(1+ )
10
1
=
1200×
10
11
120
1
=
1320
(元)
1320×(1- )
10
1
=
1320×
10
9
132
1
=
1188
(元)
人心脏的跳动次数随年龄而变化。青少年 心跳每分钟约75次,婴儿每分钟心跳的次
数比青少年多 。婴儿每分钟心跳多少次 ?
5
4
青少年每分钟心跳约( )次
75
婴儿每分钟心跳的次数比青少年多 ,多的部
分是( )的
青少年
要求的是( )每分钟心跳的次数。
婴儿
5
4
5
4
例9:
人心脏的跳动次数随年龄而变化。青少年 心跳每分钟约75次,婴儿每分钟心跳的次
数比青少年多 。婴儿每分钟心跳多少次 ?
5
4
青少年:
婴儿:
75次
比青少年多
5
4
?次
人心脏的跳动次数随年龄而变化。青少年 心跳每分钟约75次,婴儿每分钟心跳的次
数比青少年多 。婴儿每分钟心跳多少次 ?
5
4
5
4
婴儿每分钟心跳的次数比青少年多
5
4
婴儿每分钟心跳的次数比青少年多的占青少年的
=
+
×
婴儿每分钟心跳的次数
青少年的心跳次数
青少年的心跳次数
5
4
人心脏的跳动次数随年龄而变化。青少年 心跳每分钟约75次,婴儿每分钟心跳的次
数比青少年多 。婴儿每分钟心跳多少次 ?
5
4
=
+
×
婴儿每分钟心跳的次数
青少年的心跳次数
青少年的心跳次数
5
4
75
75
+
×
5
4
5
4
婴儿每分钟心跳的次数比青少年多
5
4
婴儿每分钟心跳的次数比青少年多的占青少年的
=
+
×
婴儿每分钟心跳的次数
青少年的心跳次数
青少年的心跳次数
5
4
75
75
+
×
5
4
列数量关系式的方法
118
109
蝗虫每分钟振动次数比蜜蜂少
118
109
蝗虫每分钟振动次数比蜜蜂少的占蜜蜂的
=
-
×
蝗虫每分钟振动次数
蜜蜂每分钟振动次数
蜜蜂
每分
钟振
动次
数
118
109
236
236
-
×
118
109
3
1
鸭的孵化期比鸡长
3
1
鸭的孵化期比鸡长的占鸡的孵化期的
=
+
×
鸭的孵化期
鸡的孵化期
鸡的孵化期
3
1
21
21
+
×
3
1
小明每天早晨锻炼20分钟,小华每天早晨锻炼的时间比小明多
,小华每天早晨锻炼多长时间?
4
1
做解决问题先看单位,这里单位不需要换算。
找出解题的关键
这句话我们可以这样理解
小华每天早晨锻炼时间比小明多的时间占小明每天锻炼时间的
4
1
=
×
小华每天比小明多锻炼的时间是
4
1
20×
=
4
1
=
5
20×
1
5
(分钟)
而问题是
所以应用小明每天跑的时间加上小华比小明多跑的时间
20+
4
1
20×
=
20+
4
1
=
5
20×
1
(分钟)
25
答:略
有两筐苹果,第一筐重30千克,如果从第一筐中取出 千克放入第二筐,则两筐苹果同样重。两筐苹果一共重多少千克?
2
1
30千克
第一筐
?千克
第二筐
一 千克
2
1
十 千克
2
1
=
这其实是告诉我们第二筐比第一筐少2个 千克。
2
1
有两筐苹果,第一筐重30千克,如果从第一筐中取出 千克放入第二筐,则两筐苹果同样重。两筐苹果一共重多少千克?
2
1
第一筐
第二筐
一 千克
2
1
十 千克
2
1
=
这其实是告诉我们第二筐比第一筐少2个 千克。
2
1
所以第二筐的重量:30 – 2× =29(千克)
2
1
问题问的是两筐苹果一共重多少千克?那就用第一筐的加第二筐的就行了。
列式为:30 +29=59(千克)答:略
(1)18米减去 是多少米?
6
5
(2)18米减去 米是多少米?
6
5
易混的题
(3)18减去 是多少?
6
5
(4)18减去它的 是多少?
6
5
18米减去 是多少米?
18 -
6
5
18米减去 米是多少米?
6
5
18 ×
6
5
=18 -15
=3(米)
18 -
6
5
=17
(米)
6
6
-
6
5
6
1
=17
18减去 是多少?
6
5
18减去它的 是多少?
6
5
18 -
6
5
=17
6
6
-
6
5
6
=17
1
18 -
18 ×
6
5
=18 -15
=3
1米长的铁丝,用去 ,又用去 米,共用去了多少米
1米长的铁丝,用去 米,又用去剩下的 ,共用去了多少米
1 ×
+
3
1
=
3
1
3
1
+
3
1
=
3
2
(米)
+
3
1
=
3
1
3
1
+
3
2
×
3
1
(米)
(1 - )×
3
1
=
3
1
+
9
2
=
9
5
3
2
9米长的绳子用去 ,用去多少米?
9米长的绳子用去 米,还剩多少米?
3
2
9米长的绳子用去 ,还剩全长的几分之几?
3
2
正确的为:9× (1- )
3
2
√
×
1-
3
2
3
2
列式为9×
3
2
列式为9-
3
2
列式为9×(1- )
3
2
9米长的绳子用去 ,还剩多少米?
√
3
2
列式为9×
×
分数乘法
分 数 乘 法
分数乘整数
分数乘分数
小数乘分数
整数运算定律推广到分数乘法
分数乘法应用题
分数乘整数知识点
1、分数乘整数的意义与整数乘法的意义相同,就是求几个相同加数和的简便运算。
2、分数与整数相乘,用分数的分子与整数相乘的积做分子,分母不变。
注:计算时能约分的要先约分再计算出结果。
4
3
2× =
4
3
2× =
2
1
2
3
×
10
3
4
如 的意义是
4个 是多少
10
3
分数乘整数知识点:强调
1、一个整数乘分数有时表示几个相同的分数相加,有时表示这个整数的几分之几
×
10
3
4
如 的意义可以是
也可以是 只有有具体情境时才能分到底是几个相同加数的和还是这个数的几分之几。
4个 是多少
10
3
4的 是多少
10
3
分数乘整数知识点:强调
如第2页课本例1,就只能是3个 相加是多少?
4
1
所以配套练习册19页的我会判断的第一小题
9
2
×
9
1
5
计算方法相同,意义也是
5× 和
9
1
相同的这句话是正确的。
而第3页的例2的第3小题则只能是求12的 是多少?
1、整数乘法的意义:(
)
求几个相同加数和
的简便运算
2、同分母分数相加减只把( )相加减( )不变,计算结果( )
分子
分母
能约分的要约成最简分数
分数乘整数练习
3、分数乘整数的意义与( )的意义相同,就是求( )的( )。
求几个相同加数和
整数乘法
简便运算。
4、分数乘整数的计算法则
①分数与整数相乘,用( )做分子,( )不变。
②计算时( )再计算出结果。
分数的分子与整数相乘的积
分母
能约分的要先约分
5、分数乘整数,用( )作分子,( )不变。
分数的分子与整数相乘的积
分母
9
7
+
9
7
+
9
7
=( )×( )=( )
2
1
+
2
1
=( )×( )=( )
9
7
3
3
7
2
1
2
3
1
1
6、
1
1
8
7
+
8
7
+
8
7
=( )×( )=( )
8
7
3
8
21
×
10
3
4
7、 的意义是( )
4个 是多少
10
3
×
8
7
6
的意义是( )
4的 是多少
10
3
6个 是多少
8
7
6的 是多少
8
7
平方米=( )平方分米
时=( )分
( )与整数乘法的意义相同。
1、
2、
分数乘整数的意义
1平方米=100平方分米
由平方米到平方分米是由高级单位到低级单位,要乘它们的进率100,
25
8
×
100
25
8×100
=
=32
1
4
32
1时=60分
由时到分是由高级单位到低级单位,要乘它们的进率60,
4
3
×
60
4
3×60
=
=45
1
15
45
一根绳子长
米,3根这样的绳子共长( )米;这根
长( )米。
绳子的
3、
3根共长多少就是求3个 是多少
10
9
×
3
10
9×3
=
=
10
27
(米)
这根绳子的 长多少米,就是求 的 是多少。
10
9
×
10×3
9×1
=
=
10
3
(米)
3
1
1
3
10
27
10
3
比30多 的数是( )比35的 多3的数是( )。
4、
7
2
×
35
7
35×2
=
=
13
6
1
7
2
比30多 ,这里没有说是30的 ,所以这里的两个数都是确定的数值,可以直接相加。
6
1
6
1
30
6
1
比35的 多3,这里的 是30的 ,在这里是一个比率不是一个确定的值。所以列式为
7
2
7
2
7
2
+3
+3
1
5
13
8
3
×
3
4
×
4
3
8
3
×
8
5
×
6
5
8、计算
8
3×3
=
8
9
=
8
3×8
=
=3
1
1
4
4×3
=
=3
1
1
6
5×5
=
6
25
=
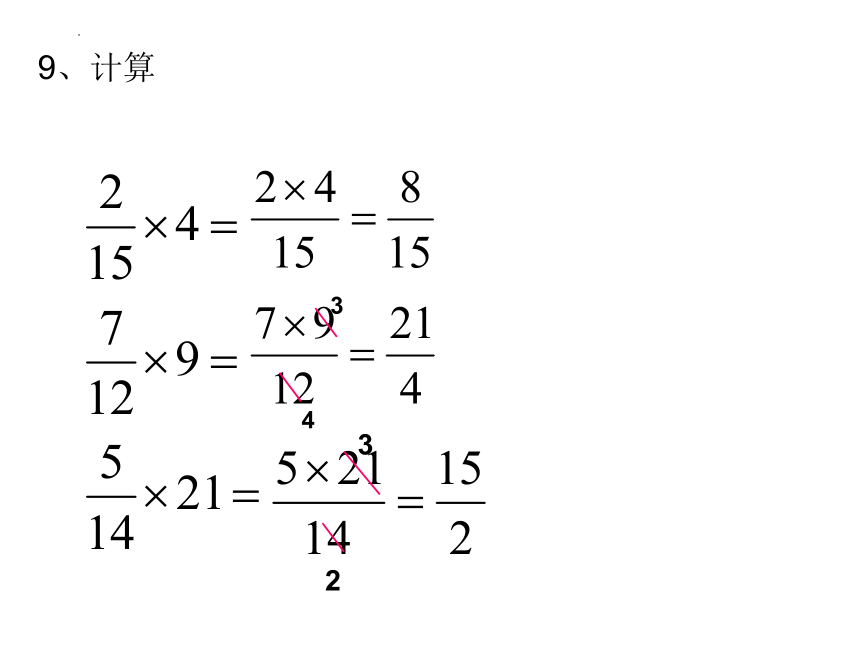
9、计算
3
4
3
2
10
3
3× =
10
3×3
=
10
9
4
3
2× =
4
2×3
=
2
3
2
1
4
3
2× =
4
3
2× =
2
1
2
3
1
0
7
2
×
14
2
= ×
7
16
14
1
=
1
16
2
= 32
2
×
7
2
2
=
7
2×7+2
=
7
16
带分数乘一个数,要先把带分数化成假分数后再按分数乘法的计算方法进行计算。
8
3
×
8
1
= ×
8
11
8
1
=
1
11
1
= 11
1
×
8
3
1
=
8
1×8+3
=
8
11
带分数乘一个数,要先把带分数化成假分数后再按分数乘法的计算方法进行计算。
10、列式计算
(1)3个 相加是多少?
8
3
8
3
×3=
8
3×3
=
8
9
(2) 的15倍是多少?
5
2
5
2
×15=
5
2×15
=
1
6
1
3
=6
(3)3 的 是多少?
8
3
3× =
8
3×3
=
8
9
(4)15的 是多少?
5
2
5
2
15× =
5
15×2
=
1
6
1
3
=6
8
3
一张报纸的厚度大约是 mm 。100张这样的报纸叠放在一起厚度大约是多少厘米。
5
2
任何解决问题都应先看单位名称是否相同,如不相同一定要换算单位。
100
× =
5
2
100
×
5
2
20
1
(mm)
=4(厘米)
答:略
=40
解决问题
分数乘分数的知识点
1、分数乘分数的意义就是求这个数的几分之几是多少。
注:求一个数的几倍或是求这个数的几分之几都要用乘法,也就是说问题中的“的”字要换成乘号。
如12的 是多少?
3
1
列式为12×
3
1
如12的3 倍是多少?
列式为12×3
× 的意义是( )
5
1
2
1
的 是多少
5
1
2
1
1、一个数乘分数的意义就是( )
求这个数的几分之几是多少
10
3
3×
3、 的意义是( )
3的 是多少
10
3
分数乘分数的练习
2、分数与分数相乘,用( )做分子,( )做分母。
分子与分子相乘的积
分母与分母相乘的积
9
1
×
的意义是( )
的 是多少
9
1
9
5
9
5
4、路程=( )
速度×时间
3个 是多少
10
3
5、从 吨水泥中运走 ,还剩下( )吨;从 吨水
泥中运走 吨,还剩下( )吨。
4
3
5
2
4
3
5
2
从 吨中运走 ,这里是 吨的 ,是把水泥
的总数量看做单位“1”,平均分成5份,运走了其中的两份,所以还剩下其中的3份。可以列式为:
4
3
5
2
4
3
5
2
4
3
-
4
3
=
×
5
2
4
3
=
×
5
3
20
9
(吨)
20
9
从 吨水泥中运走 ,还剩下( )吨;从 吨水泥中
运走 吨,还剩下( )吨。
4
3
5
2
4
3
5
2
从 吨中运走 吨,这里运走的是 吨,是一个
确定的数值,求还剩下多少吨,就用数量关系式:
总数-运走的=剩下的
4
3
5
2
5
2
4
3
-
=
5
2
20
15
=
-
20
8
20
7
(吨)
20
7
20
9
6、李伯伯家有一块 公顷的地。种土豆的
面积占这块地的 ,种土豆的面积是多少
公顷?
2
1
这里是把( )看做单位“1”,是( )
要求( ),也就是求
( )
列式计算( )
5
1
这块地的面积
2
1
公顷
种土豆的面积是多少公顷
的 是多少
5
1
2
1
× = ( 公顷 )
5
1
2
1
10
1
×2 ○
8×
○8
×
○
×
○
×
×1 ○
2
1
×
8
1
( + )
5
1
2
1
×
8
1
+
5
1
○
2
1
9、
一个数乘一个大于1的数所得的积大于它本身
>
一个数乘一个小于1的数所得的积小于它本身
<
一个数乘一个小于1的数所得的积小于它本身
<
>
一个数乘1的数所得的积等于它本身
=
2
1
×
8
1
+
2
1
×
8
1
<
( + )
5
1
2
1
×
8
1
+
5
1
○
5
1
×
8
1
○
<
2
1
8
3
×
3
4
×
4
3
3
2
×
3
2
5
2
×
5
2
8
3
×
8
5
×
6
5
3
2
+
3
2
5
2
+
5
2
6、计算
8
3×3
=
8
9
=
8
3×8
=
=3
1
1
4
4×3
=
=3
1
1
6
5×5
=
6
25
=
3×3
2×2
=
9
4
=
3
2+2
=
3
4
=
5×5
2×2
=
25
4
=
5
2+2
=
5
4
=
7
2
×
2
= ×
7
16
1
=
7×1
2
5
=
2
×
带分数乘一个数,要先把带分数化成假分数后再按分数乘法的计算方法进行计算。
8
5
8
5
7
10
8
3
×
2
1
= ×
8
11
1
=
1×3
11
1
1
×
带分数乘一个数,要先把带分数化成假分数后再按分数乘法的计算方法进行计算。
3
2
3
8
=
3
11
8、列式计算
(1) 公顷 的 是多少?
12
5
12
5
× =
12×7
5×4
=
21
5
(2) dm的 是多少分米?
3
2
1
3
(公顷)
7
4
7
4
5
4
3
2
× =
5
4
3
2
× =
5
4
15
8
(分米)
一个长方形的长是 m 。宽是长的 。
这个长方形的面积是多少平方米。
6
5
长方形的面积=长×宽。
宽:
×
6
5
×
6
5
2
1
=
答:略
10
9
这里知道长,但不知道宽要先求宽
10
9
=
10
9
2
3
4
3
面积:
×
10
9
4
3
=
10×4
9×3
=
40
27
(米)
(米 )
解决问题
每千克小麦可磨成面粉 kg。 t 小麦
或磨成面粉多少千克?
2
3
×1000
×1000
1
500
=1500
答:略
5
4
2
3
=
2
3
换算单位:
×1500
5
4
=
5
4
=1200
(千克)
(千克)
任何解决问题都应先看单位名称是否相同,如不相同一定要换算单位。
×1500
1
300
修一条长6km的道路,第一期完成了这
条路的 ,第二期完成了这条路的 。第一期比第二期多修了多少千米?
10
3
5
2
任何解决问题第一步都应先看单位名称是否相同,如不相同一定要换算单位。这里不需要换算。
第二步就是找重要的数学信息,或者说是解题关键。
修一条长6km的道路,第一期完成了这
条路的 ,第二期完成了这条路的 。第一期比第二期多修了多少千米?
10
3
5
2
得出第一个数量关系式第一期完成的等于这条路
总长的 可以表示为(一)=总长×
5
2
5
2
得出第二个数量关系式第二期完成的等于这条路
总长的 可以表示为(二)=总长×
10
3
10
3
修一条长6km的道路,第一期完成了这
条路的 ,第二期完成了这条路的 。第一期比第二期多修了多少千米?
10
3
5
2
最后是看问题,让我们求什么?
这里是让我们求第一期比第二期多修了多少千米?
同样存在一个数量关系式,第一期比第二期长的千米数等于第一期的减第二期的可表示为:
(一)比(二)多的=(一)-(二)
修一条长6km的道路,第一期完成了这
条路的 ,第二期完成了这条路的 。第一期比第二期多修了多少千米?
10
3
5
2
总长×
5
2
总长×
10
3
(一)比(二)多的=(一)-(二)
=
=
由此我们可以列式为:
6×
5
2
-
6×
10
3
=
6×
10
1
3
5
=
5
3
(千米)
答:略
小数乘分数的知识点
1、小数乘分数的意义就是求这个数的几分之几是多少。
1.2× 的意义是( )
5
1
1.2的 是多少
5
1
2、计算小数乘分数时,可以把小数转化成分数进行计算;在计算小数乘分数时,如果小数能和分数的分母约分,可以先约分再计算,这样可以使计算简便。
如:
7
2
×
2.8
7
2
×
2.8
= ×
2.8=
7
2
10
28
5
14
5
14
=
5
14
1
2
= ×
1
2
5
2
=
5
4
7
2
2.8
= ×
7
2
1
0.4
= ×
1
2
= 0.8
×
2.8
0.4
72
17
×
17
16
21
20
×0.42
44
25
×1.1
4
1
0.32×
7
5
×5.6
12
7
×0.36
17
3
×5.1
计算
72
17
×
17
16
=
72
17
×
17
16
=
1
1
9
2
9
2
21
20
×0.42
=
21
20
×0.42
=0.4
1
0.02
44
25
×1.1
=
44
25
×1.1
=
4
0.1
4
2.5
=
8
5
4
1
0.32×
=
4
1
0.32×
=0.08
1
0.08
7
5
×5.6
=
7
5
×5.6
=4
1
0.8
12
7
×0.36
=
12
7
×0.36
=
1
0.03
17
3
×5.1
=
17
3
0.21
=0.9
1
0.3
×5.1
1、每千克花生可榨油0.38千克。 吨花生米可榨油多
少千克?
4
5
这里单位不同应换算成相同的单位后再进行了计算
4
5
1吨=1000千克,由大单位到小单位要乘它们的进率
×1000=
4
5
×1000=
1
250
1250千克
1250×0.38=
475
答:略
(千克)
解决问题
2、码头有125.5吨货物,上午运走总数的 ,下午
运走的是上午的 ,下午运走总数的几分之几?下午运走多少吨?
5
2
4
3
上午运走总数的 ,是把总数看做单位“1”,平均分
成5份,上午运走了这样的2份。
5
2
下午运走的是上午的 ,是把上午运走的数量看做
单位“1”,平均分成4份,下午运走了这样的3份。
4
3
下午运走的是上午的 也就是 的
4
3
5
2
4
3
上午运走的
125.5吨
下午运走的=
总数
上午运走的
=总数×
5
2
上午运走的数量
4
3
=
总数×
5
2
×
=
1
(1)下午运走总数的几分之几?
=
4
3
5
2
×
=
4
3
5
2
×
1
2
10
3
(2)下午运走了多少吨?
10
3
125.5×
=
10
3
125.5×
=37.65(吨)
1
12.55
答:略
答:略
2
1
找规律
3
1
9
2
, , ,( ),( )
3
1
÷
=
2
1
3
1
=
× 2
3
2
9
2
÷
=
3
1
9
2
=
× 3
3
2
3
1
×
3
2
×
3
2
×
3
2
27
4
×
3
2
81
8
整数运算定律推广到分数乘法
1、分数乘加、乘减混合运算与整数混合运算顺序相同。
(1)、如果只有乘除或只有加减,按从左往右的顺序依次进行计算
(2)、如果既有乘除又有加减,要先算乘除再算加减
(3)、有括号的要先算括号里面的。
5 -
6
1
×( )
3
2
这里运用乘法分配律也不简便,所以就按照有括号的要先算括号里面的来进行运算。
=
2
6
1
×( - )
15
3
3
整数化成分数,用整数乘分母的积做分子。
=
×
6
1
=
18
13
3
13
×5
2
1
×
2
1
同一级运算按从左往右的顺序依次进行计算。
=
×5
2
1
×
1
×
2
用不到的数字及符号要落下来。
=
×5
4
1
=
4
5
2
1
+
2
1
×5
既有乘除又有加减,要先算乘除再算加减。
=
2
5
用不到的数字及符号要落下来。
=
2
1
=
2
1+5
2
1
+
1
×5
2
+
=3
同分母分数相加,只把分子相加,分母不变。
8
3
+
8
7
×7
既有乘除又有加减,要先算乘除再算加减。
=
8
3
用不到的数字及符号要落下来。
=
8
49
=
8
52
8
3
+
7
×7
8
+
=
同分母分数相加,只把分子相加,分母不变。
13
2
13
2
能约分的一定要约成最简分数。
3
2
+
3
1
×
既有乘除又有加减,要先算乘除再算加减。
=
5
1
用不到的数字及符号要落下来。
=
3
2
=
15
10
3
2
+
1
×3
3×5
+
=
异分母分数相加,先把它们通分成同分母分数,再按同分母分数的方法进行计算。
5
3
+
15
3
15
13
1
1
整数运算定律推广到分数乘法
2、整数乘法的运算定律对于分数乘法同样适用。
(1)、乘法交换律:交换两个因数的位置积不变。用字母表示:a×b=b×a
2
1
×
8
1
2
1
×
8
1
○
=
2
1
×
100
19
×
8
5
=
100
19
×
×
=
2×1×8
19×1×5
=
16
95
50
8
5
1
50
1
2
×
100
19
×
8
5
=
100
19
×
×
=
2×8×1
19×1×5
=
16
95
50
8
5
1
50
5
2
20
1
整数运算定律推广到分数乘法
2、整数乘法的运算定律对于分数乘法同样适用。
(a×b)×c=a×(b×c)
2
7
×
3
5
3
5
×
2
7
○
=
7
3
(2)、乘法结合律:先把前两个相乘再与第三个数相乘或先把后两个数相乘再与第一个数相乘,积不变:用字母表示为:
( )
×
7
3
×
( )
×
9
14
×
23
7
=
9
14
×
×1
×
=
23
7
=
23
7
14
9
14
9
23
7
1
1
1
1
×
9
14
×
23
7
=
9
14
×
1×
×
=
23
7
=
23
7
14
9
14
9
23
7
1
1
1
1
整数运算定律推广到分数乘法
2、整数乘法的运算定律对于分数乘法同样适用。
(3)、乘法分配律:两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加,积不变。
(a+b)×c=a×c+b×c
○
=
×
8
1
2
1
+
1
5
( )
2
1
+
1
5
×
8
1
8
1
×
87×
86
3
要用简便算法,那就要尽量约去分母,分母是86,就想办法让87变成86。87=86+1
=(86+1)×
86
3
=86× 1×
86
3
=
86
3+
3
86
+
=3
利用乘法分配律
用简便算法
1
1
3
86
3
整数与分数相加,直接组合在一起就行。
4.8×
6
1
12
( )
-
1
43×
42
5
16
3
-
8
7
×
8
7
99
×
5
2
+
5
2
101
×
10
7
-
10
7
乘法分配律专题训练
75×
+0.75×26
4
3
4
3
-
×
9
5
+
3
1
3
1
9
4
×
17×
8
3
47×
48
43
11
×
12
11
+
12
11
× 12
4
2
3
1
( )
-
101×
5
4
4.8×
6
1
12
1
=
1
5
24
×( - )
1
12
6
=
×
5
24
= -
5
4
6
1
( )
-
4.8=
48
24
5
24
=
10
5
×
5
24
12
1
-
4
1
48是6的倍数,也是12的倍数,所以这个题可以用乘法分配律来计算。
2
1
5
2
=
5
2
4.8×
6
1
12
1
=
×
4.8
= 0.8 - 0.4
6
1
( )
-
×
4.8
12
1
-
0.8
1
48是6的倍数,也是12的倍数,所以这个题可以用乘法分配律来计算。
0.4
1
= 0.4
43×
42
5
=
5
( 42 + 1)×
42
=
×
42
= +
5
42
5
×
1
42
5
+
1
1
整数43比分母42多1,我们可以把它写成42+1的形式。
42
5
=
42
5
5
16
3
-
8
7
×
=
8
7
=(1- )
16
3
=
16
13
16
3
-
7
1×
8
×
=
91
128
8
7
7
×
8
×
8
7
17×
8
3
=
3
( 16 + 1)×
8
=
×
16
= +
6
8
3
×
1
8
3
+
2
1
整数17比分母的2倍多1,我们可以把它写成16+1的形式。
8
3
=
8
3
6
99
×
5
2
+
=
5
2
=(99+1 )
=
100
5
2
+
2
×99
5
×
=
40
5
2
1
×
×
5
2
20
1
101
×
10
7
-
10
7
= (101 - 1 )
=
100
×
=
70
10
7
×
10
7
10
1
×1
11
×
12
11
+
=
12
11
=(11+1 )
=
12
12
11
+
11
×11
12
×
=
11
12
11
1
×
×
12
11
1
1
× 12
4
2
3
1
=
×
3
2
= 8 - 3
12
( )
-
×
4
1
12
-
4
1
3
1
= 5
101×
5
4
=
4
( 100 + 1)×
5
=
×
100
= +
80
5
4
×
1
5
4
+
20
1
5
4
=
5
4
80
47×
48
43
=
43
( 48 - 1)×
48
=
×
48
= -
43
48
43
×
1
48
43
-
1
1
48
43
=
48
5
42
×
9
5
+
3
1
=( + )
=
1
×
=
3
1
×
3
1
3
1
9
4
×
9
5
9
4
3
1
75×
+0.75×26
4
3
=( 75 + 26 - 1 )
=
100
×
=
4
3
×
4
3
4
3
-
75
=
75×
+ ×26
4
3
4
3
-
1×
4
3
25
1
39
25
×
30
13
=
39
25
×
30
13
=
5
6
3
1
18
5
11
6
×10
=
11
6
×10
=
3
2
×
15
7
15
7
2
×
1
11
28
100
19
×50
=
100
19
×50
=
2
1
×
8
3
8
3
×
16
57
9
7
-
=
27
14
=
×
3
2
7
2
-
7
2
=
189
98
189
54
-
189
44
计算出错较多的题
×
2
1
○
6
5
2
1
一个数乘小于1的数所得的积一定小于它本身。
<
×
5
○
3
1
3
1
<
×5
×
6
8
7
○
>
×
6
7
8
1
○
<
×
8
1
2
1
+
1
5
( )
2
1
+
1
5
×
8
1
5
3
3
5
一个数乘大于1的数所得的积一定大于它本身。
2
1
×
8
1
+
2
1
×
8
1
<
( + )
5
1
2
1
×
8
1
+
5
1
○
5
1
×
8
1
○
<
2
1
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
(1)两周一共卖出总数的几分之几?
(2)两周一共卖出多少双?
(3)还剩多少双?
5
1
8
3
任何解决问题第一步都应先看单位名称是否相同,如不相同一定要换算单位。这里不需要换算。
第二步就是找重要的数学信息,或者说是解题关键。
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
5
1
8
3
得出第一个数量关系式第一周卖出的的等于
总数的 可以表示为(一)=总数×
5
1
5
1
得出第二个数量关系式第二周卖出的等于
总数的 可以表示为(二)=总数×
8
3
8
3
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
(1)两周一共卖出总数的几分之几?
(2)两周一共卖出多少双?
(3)还剩多少双?
5
1
8
3
最后是看问题,让我们求什么?三个问题一个一个的解决。
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
(1)两周一共卖出总数的几分之几?
5
1
8
3
同样存在一个数量关系式,第一周的加第二周的就是两周一共卖出的。
两周一共卖出的=(一)+(二)
总数×
5
1
总数×
8
3
=
=
这里问的是卖出总数的几分之几,所以把总数看作单位“1”进行计算。
1×
1×
+
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
(1)两周一共卖出总数的几分之几?
5
1
8
3
5
1
8
3
=
+
40
8
40
15
=
+
40
23
答:略
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
(2)两周一共卖出多少双?
5
1
8
3
同样存在一个数量关系式,第一周的加第二周的就是两周一共卖出的。
两周一共卖出的=(一)+(二)
总数×
5
1
8
3
=
=
总数×
+
这里是求确定的数值,可列式为:
600×
5
1
+
600×
8
3
=
600×
40
23
15
1
=
345(双)
答:略
某鞋店进来皮鞋600双。第一周卖出总数
的 ,第二周卖出总数的 。
(3)还剩多少双?
5
1
8
3
同样存在一个数量关系式,总数减去卖出的等于剩下的剩下的=总数 - 卖出的
600
-
345
=
225(双)
答:略
图书室新进一批图书,其中故事书占总数
的 ,科技书的本数是故事书的 ,文
艺书的本数是科技书的 。文艺书的本数占总数的几分之几 。
20
3
5
3
9
2
任何解决问题第一步都应先看单位名称是否相同,如不相同一定要换算单位。这里不需要换算。
第二步就是找重要的数学信息,或者说是解题关键。
图书室新进一批图书,其中故事书占总数
的 ,科技书的本数是故事书的 ,文
艺书的本数是科技书的 。文艺书的本数占总数的几分之几 。
20
3
5
3
9
2
故事书的本数=总数×
20
3
科技书的本数=故事书的本数×
5
3
文艺书的本数=科技书的本数×
9
2
故事书的本数=总数×
20
3
科技书的本数=故事书的本数×
5
3
文艺书的本数= 科技书的本数 ×
9
2
最后让我们求科技书的本数占总数的几分之几?
我们可以依次替代
总数×
20
3
总数×
20
3
×
5
3
最后仅是让我们求占总数的几分之几,不是确定的数值,所以把总数看作单位“1”
1
9
2
×
20
3
×
5
3
=
9
2
×
20
3
×
5
3
=
10
1
1
3
50
1
1
1
答:略
学校将300本图书分给六年级的三个班,六(1)班分到
六(2)班分到 ,剩下的分给六(3)班。六(3)班
分到多少本图书?
4
1
5
2
六(2)=总数×
4
1
这里说六(二)班分到 ,没说是说的,就是
顺着来的,也就是也是总数的 ,列式为
5
2
5
2
六(1)=总数×
5
2
六(3)=总数 - 六(1)-六(2)
300 - 300× -300×
4
1
5
2
学校将300本图书分给六年级的三个班,六(1)班分到
六(2)班分到 ,剩下的分给六(3)班。六(3)班
分到多少本图书?
4
1
5
2
300 - 300× -300×
4
1
5
2
=300 - 75 - 120
=105(本)
300 ×(1- - )
4
1
5
2
=300 ×
20
7
=105(本)
答:略
分数乘法应用题
做任何应用题都是按以下三步去做:
(1)、审题:认真读题,看单位是否需要换算。找重要的数学信息。
(2)、分析:对找到的数学信息进行分析,写出相应的数量关系式。
(3)、解题:看问题让我们求的是什么,找能解答问题的数量关系式进而解题。
注:本单元重点教我们找单位“1”,谁的几分之几谁就是单位“1”;或者是和谁比较谁就是标准,就要把它平均分,那么它就是单位“1”
(4)、检查、验算。
梨树棵数的 与苹果树同样多,是把( )
看作单位“1”。如果梨树有28棵,那么苹果树有( )棵。
7
3
谁的 ,谁就是单位“1”,这里说的是梨树棵数的
所以这里是把梨树的棵数看作单位“1”。
梨树的棵数
知道梨树的棵树,求苹果树的棵数,还是要用到上面那句话
28×
7
3
7
3
7
3
×
=
的棵数
=
28×
7
3
=
1
4
12
(棵)
12
甲数比乙数多 ,是把甲数看作单位“1” ( )
5
1
补充完整是:甲数比乙数多的占乙数的 ,这里是把
乙数平均分成5份,甲比它多这样的1份,把乙平均分了,那么乙就是单位“1”所以这句话是错的。
5
1
×
甲数的 等于乙数的 ,则甲数小于乙数。 ( )
5
4
3
2
×
=
×
=1
=
4
5
=
2
3
4
6
<
=
这里这个题成立的先决条件是这两个数都不为零,但是它没有就所以这个题目是错的。如果说了它俩都不为零就是对的。
×
实际产量比原计划多 。这句话是指实际比原计划多的产量是
( ) 的
4
1
补充完整是:实际产量比原计划多的占原计划的 ,所以选B
4
1
4
1
A、实际产量 B、原计划产量 C、多的产量
B
6
5
×15
=
6
5
=
5
×15
2
2
25
1
1、甲数是乙数的 ,是把( )看作单位“1”
5
2、甲数的 是乙数,是把( )看作单位“1”
1
5
乙数
甲数
(1)、一块布用去 中单位“1”是( )
5
3
(2)、吃了一袋大米的 :( )
8
5
(3)、运走了一堆煤的 ( )
9
7
(4)、看了一本书的 :( )
6
5
这块布的总长
这袋大米的总重量
这堆煤的总重量
这本书的总页数
找单位“1”
一个大棚共480m ,其中一半种各种萝卜,
红萝卜地的面积占整块萝卜地的 ,红萝卜地有多少平方米 ?
4
1
整个大棚的面积是( )
2
1
480平方米
萝卜地的面积占整个大棚面积的( )
一半也就是
红萝卜地的面积占萝卜地面积的( )
4
1
要求的是( )面积
红萝卜地的
例8:
一个大棚共480m ,其中一半种各种萝卜,
红萝卜地的面积占整块萝卜地的 ,红萝卜地有多少平方米 ?
4
1
480平方米
各种萝卜地占大棚面积的
2
1
红萝卜地占萝卜地面积的
4
1
一个大棚共480m ,其中一半种各种萝卜,
红萝卜地的面积占整块萝卜地的 ,红萝卜地有多少平方米 ?
4
1
先求( )这里是把( )看作单位“1”,要求( ),也就是
求( ),列式为(
2
1
种萝卜的地的面积
480的 是多少
大棚的总面积
种萝卜的地的面积
2
1
480× =480× =240( m )
2
1
1
240
一个大棚共480m ,其中一半种各种萝卜,
红萝卜地的面积占整块萝卜地的 ,红萝卜地有多少平方米 ?
4
1
再求( )这里是把( )看作单位“1”,要求( ),也就是求
( ),列式为(
4
1
种红萝卜的地的面积
240的 是多少
种各种萝卜的地的面积
种红萝卜的地的面积
4
1
240× =240× =60( m )
4
1
1
60
一个大棚共480m ,其中一半种各种萝卜,
红萝卜地的面积占整块萝卜地的 ,红萝卜地有多少平方米 ?
4
1
4
1
480× ×
8
1
1
60
2
1
=480×
=60(m )
答:略
奶牛场每头奶牛平均日产牛奶 吨,42
头奶牛100天可产奶多少吨?
这里要先求( )这里是把
( )看做单位“1”,是( )
要求( ),也就是求
( )
列式计算( ) 再
求( ),
列式计算( )
42头牛一天产奶多少吨
50
1
吨
每头奶牛每天的产奶量
42个 是多少
50
1
50
1
42头牛一天产奶多少吨
×42= = (吨)
50
1
50
1×42
21
25
25
21
42头牛100产奶多少吨
×100= =84 (吨)
25
21
25
21×100
4
1
六一班有男生25人,比女生多2人,全班人数的 已达到《体
育锻炼标准》,达到《体育锻炼标准》的有多少人?
8
5
做解决问题先看单位,这里单位不需要换算。
找出解题的关键
这句话我们可以这样理解
全班总人数的 已达到《体育锻炼标准》
8
5
=
×
全班人数等于男生人数加女生人数
男生比女生多2人,就是女生比男生少2人所以应用25减2求女生人数
(25+25-2)
8
5
×
=
48
8
5
=
6
×
1
(人)
30
答:略
小军读一本315页的《哈利波特》第一天读了全书的 ,第二
天读了剩下的 ,第二天读了多少页?
7
2
做解决问题先看单位,这里单位不需要换算。
找出解题的关键
第一天读了全书的
8
5
=
×
问题是求第二天读了多少页,就用第二个数量关系式,只要知道剩下多少页就能求出,但题目中没有说剩下多少,我们只能用总数减去第一天看的求出剩下的再进行第二步的计算。
315×(1- )
5
1
×
=
315
7
5
=
45
×
1
(页)
45
答:略
5
1
第二天读了剩下的
5
1
=
×
7
2
5
1
×
1
1
一种电视机原价1200元,先涨价 ,再降价 。现在这
种电视机每台售价多少元?
10
1
做解决问题先看单位,这里单位不需要换算。
找出解题的关键
先涨的价是原价的
10
1
=
×
最后求现价,就是先在原价的基础上加上原价的
之后再在涨后的价格的基础上再除它的
10
1
再除的价是涨价后的
10
1
=
×
10
1
10
1
1200×(1+ )
10
1
=
1200×
10
11
120
1
=
1320
(元)
1320×(1- )
10
1
=
1320×
10
9
132
1
=
1188
(元)
人心脏的跳动次数随年龄而变化。青少年 心跳每分钟约75次,婴儿每分钟心跳的次
数比青少年多 。婴儿每分钟心跳多少次 ?
5
4
青少年每分钟心跳约( )次
75
婴儿每分钟心跳的次数比青少年多 ,多的部
分是( )的
青少年
要求的是( )每分钟心跳的次数。
婴儿
5
4
5
4
例9:
人心脏的跳动次数随年龄而变化。青少年 心跳每分钟约75次,婴儿每分钟心跳的次
数比青少年多 。婴儿每分钟心跳多少次 ?
5
4
青少年:
婴儿:
75次
比青少年多
5
4
?次
人心脏的跳动次数随年龄而变化。青少年 心跳每分钟约75次,婴儿每分钟心跳的次
数比青少年多 。婴儿每分钟心跳多少次 ?
5
4
5
4
婴儿每分钟心跳的次数比青少年多
5
4
婴儿每分钟心跳的次数比青少年多的占青少年的
=
+
×
婴儿每分钟心跳的次数
青少年的心跳次数
青少年的心跳次数
5
4
人心脏的跳动次数随年龄而变化。青少年 心跳每分钟约75次,婴儿每分钟心跳的次
数比青少年多 。婴儿每分钟心跳多少次 ?
5
4
=
+
×
婴儿每分钟心跳的次数
青少年的心跳次数
青少年的心跳次数
5
4
75
75
+
×
5
4
5
4
婴儿每分钟心跳的次数比青少年多
5
4
婴儿每分钟心跳的次数比青少年多的占青少年的
=
+
×
婴儿每分钟心跳的次数
青少年的心跳次数
青少年的心跳次数
5
4
75
75
+
×
5
4
列数量关系式的方法
118
109
蝗虫每分钟振动次数比蜜蜂少
118
109
蝗虫每分钟振动次数比蜜蜂少的占蜜蜂的
=
-
×
蝗虫每分钟振动次数
蜜蜂每分钟振动次数
蜜蜂
每分
钟振
动次
数
118
109
236
236
-
×
118
109
3
1
鸭的孵化期比鸡长
3
1
鸭的孵化期比鸡长的占鸡的孵化期的
=
+
×
鸭的孵化期
鸡的孵化期
鸡的孵化期
3
1
21
21
+
×
3
1
小明每天早晨锻炼20分钟,小华每天早晨锻炼的时间比小明多
,小华每天早晨锻炼多长时间?
4
1
做解决问题先看单位,这里单位不需要换算。
找出解题的关键
这句话我们可以这样理解
小华每天早晨锻炼时间比小明多的时间占小明每天锻炼时间的
4
1
=
×
小华每天比小明多锻炼的时间是
4
1
20×
=
4
1
=
5
20×
1
5
(分钟)
而问题是
所以应用小明每天跑的时间加上小华比小明多跑的时间
20+
4
1
20×
=
20+
4
1
=
5
20×
1
(分钟)
25
答:略
有两筐苹果,第一筐重30千克,如果从第一筐中取出 千克放入第二筐,则两筐苹果同样重。两筐苹果一共重多少千克?
2
1
30千克
第一筐
?千克
第二筐
一 千克
2
1
十 千克
2
1
=
这其实是告诉我们第二筐比第一筐少2个 千克。
2
1
有两筐苹果,第一筐重30千克,如果从第一筐中取出 千克放入第二筐,则两筐苹果同样重。两筐苹果一共重多少千克?
2
1
第一筐
第二筐
一 千克
2
1
十 千克
2
1
=
这其实是告诉我们第二筐比第一筐少2个 千克。
2
1
所以第二筐的重量:30 – 2× =29(千克)
2
1
问题问的是两筐苹果一共重多少千克?那就用第一筐的加第二筐的就行了。
列式为:30 +29=59(千克)答:略
(1)18米减去 是多少米?
6
5
(2)18米减去 米是多少米?
6
5
易混的题
(3)18减去 是多少?
6
5
(4)18减去它的 是多少?
6
5
18米减去 是多少米?
18 -
6
5
18米减去 米是多少米?
6
5
18 ×
6
5
=18 -15
=3(米)
18 -
6
5
=17
(米)
6
6
-
6
5
6
1
=17
18减去 是多少?
6
5
18减去它的 是多少?
6
5
18 -
6
5
=17
6
6
-
6
5
6
=17
1
18 -
18 ×
6
5
=18 -15
=3
1米长的铁丝,用去 ,又用去 米,共用去了多少米
1米长的铁丝,用去 米,又用去剩下的 ,共用去了多少米
1 ×
+
3
1
=
3
1
3
1
+
3
1
=
3
2
(米)
+
3
1
=
3
1
3
1
+
3
2
×
3
1
(米)
(1 - )×
3
1
=
3
1
+
9
2
=
9
5
3
2
9米长的绳子用去 ,用去多少米?
9米长的绳子用去 米,还剩多少米?
3
2
9米长的绳子用去 ,还剩全长的几分之几?
3
2
正确的为:9× (1- )
3
2
√
×
1-
3
2
3
2
列式为9×
3
2
列式为9-
3
2
列式为9×(1- )
3
2
9米长的绳子用去 ,还剩多少米?
√
3
2
列式为9×
×
