数学人教A版2019必修第一册4.3 对数 课件(共28张ppt)
文档属性
| 名称 | 数学人教A版2019必修第一册4.3 对数 课件(共28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-30 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
4.3对数
4.3.1对数的概念
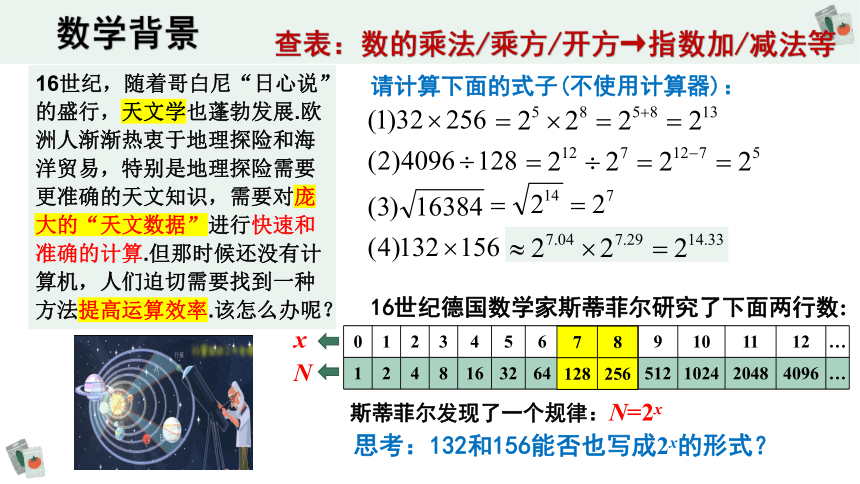
数学背景
16世纪,随着哥白尼“日心说”的盛行,天文学也蓬勃发展.欧洲人渐渐热衷于地理探险和海洋贸易,特别是地理探险需要更准确的天文知识,需要对庞大的“天文数据”进行快速和准确的计算.但那时候还没有计算机,人们迫切需要找到一种方法提高运算效率.该怎么办呢?
请计算下面的式子(不使用计算器):
16世纪德国数学家斯蒂菲尔研究了下面两行数:
0 1 2 3 4 5 6 7 8 9 10 11 12 …
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 …
斯蒂菲尔发现了一个规律:
x
N
N=2x
7 8
128 256
思考:132和156能否也写成2x的形式?
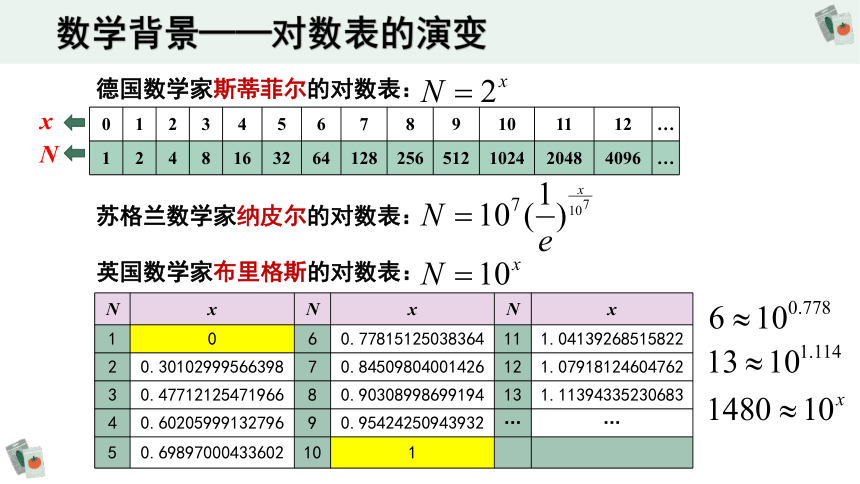
查表:数的乘法/乘方/开方→指数加/减法等
德国数学家斯蒂菲尔的对数表:
0 1 2 3 4 5 6 7 8 9 10 11 12 …
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 …
x
N
苏格兰数学家纳皮尔的对数表:
英国数学家布里格斯的对数表:
N x N x N x
1 0 6 0.77815125038364 11 1.04139268515822
2 0.30102999566398 7 0.84509804001426 12 1.07918124604762
3 0.47712125471966 8 0.90308998699194 13 1.11394335230683
4 0.60205999132796 9 0.95424250943932 … …
5 0.69897000433602 10 1
数学背景——对数表的演变
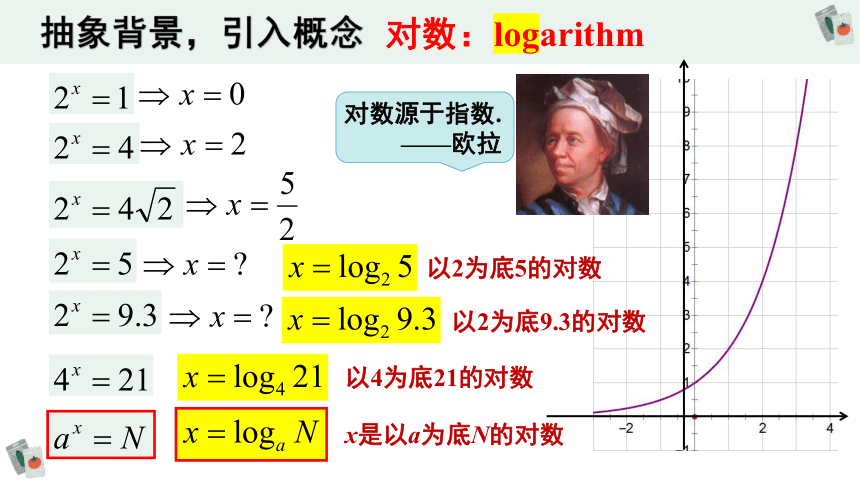
抽象背景,引入概念
以2为底5的对数
以2为底9.3的对数
以4为底21的对数
x是以a为底N的对数
对数:logarithm
对数源于指数.
——欧拉
一、对数的概念
1.对数的定义:一般地,若ax=N(a>0且a≠1),则数x叫做以a为底N的对数,
记作x=logaN(a>0且a≠1,N>0).
其中a叫做对数的底数,N叫做真数.
如:若42=16,则2=log416,读作2是以4为底16的对数.
对数:logarithm
注:①当a>0且a≠1时,ax=N x=logaN;
②对数的意义:表示指数式中的指数,减轻思维和运算负担;
③loga1= ;logaa= ;
0
1
④真数N>0:负数和0没有对数
对数和指数运算互为逆运算
⑤常用对数:以10为底的对数log10N,简记作lg N;
自然对数:以e为底的对数logeN,简记作ln N;
无理数e=2.71828…
数学文化——“对数”的评价
布里格斯说:对数的发明,延长了天文学家的寿命.
伽利略说:给我空间、时间及对数,我可以创造一个宇宙.
恩格斯说:对数的发明与解析几何的创立、微积分的建立是17世纪数学史上的3大成就.
巩固概念一
对数:logarithm
巩固概念二
对数:logarithm
巩固概念三
对数:logarithm
[练习1]求下列各式中x的值.
(1) log3(lg x) =1
(2) log2(logx 16) =2
4.3.2
对数的运算
定义延伸
N
对数恒等式
5
7
3
提出问题
Q1:引入对数之后,自然应研究对数的运算性质,怎样研究?
Q2:知道了指数与对数间的关系,能否利用指数幂运算性质得出相应的对数运算性质?
①am·an=am+n ②am÷an=am-n ③(am)n=amn
对数的运算性质
当a>0且a≠1,N>0,M>0时:
(真数)积的对数=对数的和
(真数)商的对数=对数的差
对数的实际应用
在生物领域,由碳14含量求生物死亡年数;
化学领域,对数用于计算PH值pH=-lg[H+]
在地理领域,对数用于计算地震强度;
在物理领域,对数用于测量声音的分贝10·lg(P/Pref)
里氏地震规模:M= lg (I/S)
距离震中100km处的最大水平位移为I;
“标准地震”的最大振幅为S(通常S=1μm)
每升1级,最大振幅扩大10倍,能量释放扩大30倍
对数换底公式
当a,c>0且a,c≠1,b>0时:
(底不同运算)
对数换底公式的灵活运用一
思路:底换为6
思路:底换为18
对数换底公式的灵活运用一
思路:底换为6
思路:底换为18
对数换底公式的灵活运用一
思路一:底换为2
思路二:底换为3
思路三:底换为10
思路四:底换为e
对数换底公式的灵活运用二
思路:
a=
b=
已知指数连等式时,
可化为对数式,或同时取同底对数
对数换底公式的灵活运用二
1
对数换底公式的灵活运用二
课内作业
P126-第3题(3)~(6)
第4题(3)(4)
第5题(2)(3)
第6题
FIGHTING
4.3对数
4.3.1对数的概念
数学背景
16世纪,随着哥白尼“日心说”的盛行,天文学也蓬勃发展.欧洲人渐渐热衷于地理探险和海洋贸易,特别是地理探险需要更准确的天文知识,需要对庞大的“天文数据”进行快速和准确的计算.但那时候还没有计算机,人们迫切需要找到一种方法提高运算效率.该怎么办呢?
请计算下面的式子(不使用计算器):
16世纪德国数学家斯蒂菲尔研究了下面两行数:
0 1 2 3 4 5 6 7 8 9 10 11 12 …
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 …
斯蒂菲尔发现了一个规律:
x
N
N=2x
7 8
128 256
思考:132和156能否也写成2x的形式?
查表:数的乘法/乘方/开方→指数加/减法等
德国数学家斯蒂菲尔的对数表:
0 1 2 3 4 5 6 7 8 9 10 11 12 …
1 2 4 8 16 32 64 128 256 512 1024 2048 4096 …
x
N
苏格兰数学家纳皮尔的对数表:
英国数学家布里格斯的对数表:
N x N x N x
1 0 6 0.77815125038364 11 1.04139268515822
2 0.30102999566398 7 0.84509804001426 12 1.07918124604762
3 0.47712125471966 8 0.90308998699194 13 1.11394335230683
4 0.60205999132796 9 0.95424250943932 … …
5 0.69897000433602 10 1
数学背景——对数表的演变
抽象背景,引入概念
以2为底5的对数
以2为底9.3的对数
以4为底21的对数
x是以a为底N的对数
对数:logarithm
对数源于指数.
——欧拉
一、对数的概念
1.对数的定义:一般地,若ax=N(a>0且a≠1),则数x叫做以a为底N的对数,
记作x=logaN(a>0且a≠1,N>0).
其中a叫做对数的底数,N叫做真数.
如:若42=16,则2=log416,读作2是以4为底16的对数.
对数:logarithm
注:①当a>0且a≠1时,ax=N x=logaN;
②对数的意义:表示指数式中的指数,减轻思维和运算负担;
③loga1= ;logaa= ;
0
1
④真数N>0:负数和0没有对数
对数和指数运算互为逆运算
⑤常用对数:以10为底的对数log10N,简记作lg N;
自然对数:以e为底的对数logeN,简记作ln N;
无理数e=2.71828…
数学文化——“对数”的评价
布里格斯说:对数的发明,延长了天文学家的寿命.
伽利略说:给我空间、时间及对数,我可以创造一个宇宙.
恩格斯说:对数的发明与解析几何的创立、微积分的建立是17世纪数学史上的3大成就.
巩固概念一
对数:logarithm
巩固概念二
对数:logarithm
巩固概念三
对数:logarithm
[练习1]求下列各式中x的值.
(1) log3(lg x) =1
(2) log2(logx 16) =2
4.3.2
对数的运算
定义延伸
N
对数恒等式
5
7
3
提出问题
Q1:引入对数之后,自然应研究对数的运算性质,怎样研究?
Q2:知道了指数与对数间的关系,能否利用指数幂运算性质得出相应的对数运算性质?
①am·an=am+n ②am÷an=am-n ③(am)n=amn
对数的运算性质
当a>0且a≠1,N>0,M>0时:
(真数)积的对数=对数的和
(真数)商的对数=对数的差
对数的实际应用
在生物领域,由碳14含量求生物死亡年数;
化学领域,对数用于计算PH值pH=-lg[H+]
在地理领域,对数用于计算地震强度;
在物理领域,对数用于测量声音的分贝10·lg(P/Pref)
里氏地震规模:M= lg (I/S)
距离震中100km处的最大水平位移为I;
“标准地震”的最大振幅为S(通常S=1μm)
每升1级,最大振幅扩大10倍,能量释放扩大30倍
对数换底公式
当a,c>0且a,c≠1,b>0时:
(底不同运算)
对数换底公式的灵活运用一
思路:底换为6
思路:底换为18
对数换底公式的灵活运用一
思路:底换为6
思路:底换为18
对数换底公式的灵活运用一
思路一:底换为2
思路二:底换为3
思路三:底换为10
思路四:底换为e
对数换底公式的灵活运用二
思路:
a=
b=
已知指数连等式时,
可化为对数式,或同时取同底对数
对数换底公式的灵活运用二
1
对数换底公式的灵活运用二
课内作业
P126-第3题(3)~(6)
第4题(3)(4)
第5题(2)(3)
第6题
FIGHTING
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
