数学人教A版2019必修第一册4.1 指数 课件(共17张ppt)
文档属性
| 名称 | 数学人教A版2019必修第一册4.1 指数 课件(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 815.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-30 10:46:10 | ||
图片预览






文档简介
(共17张PPT)
4.1 指数
4.1.1 n次方根与
分数指数幂
一、n次方根与根式
根式
根指数
被开方数
二、根式运算性质
口诀:开→方取本身,方→开论奇偶
巩固新知
x≤1
0
根式
分数指数幂
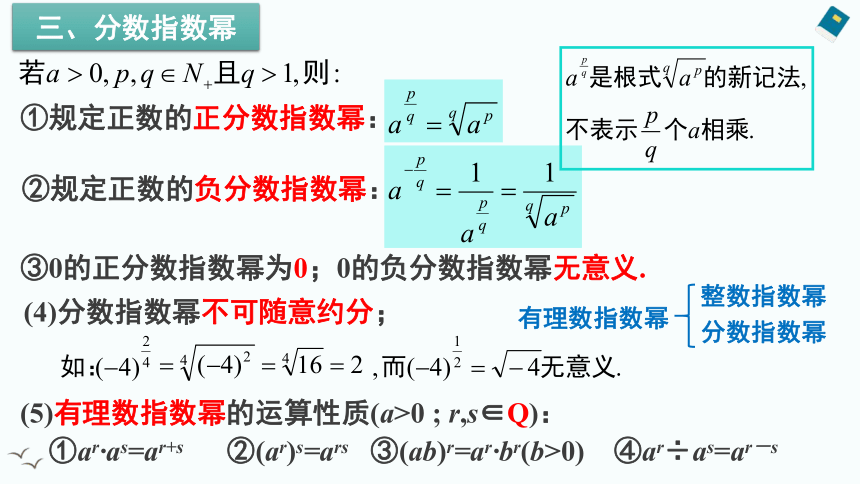
三、分数指数幂
①规定正数的正分数指数幂:
②规定正数的负分数指数幂:
③0的正分数指数幂为0;
0的负分数指数幂无意义.
三、分数指数幂
①规定正数的正分数指数幂:
②规定正数的负分数指数幂:
③0的正分数指数幂为0;0的负分数指数幂无意义.
(4)分数指数幂不可随意约分;
(5)有理数指数幂的运算性质(a>0 ; r,s∈Q):
①ar·as=ar+s ②(ar)s=ars ③(ab)r=ar·br(b>0) ④ar÷as=ar-s
整数指数幂
分数指数幂
有理数指数幂
四、有理指数幂
有理数指数幂的运算性质(a>0 ; r,s∈Q):
①ar·as=ar+s
②(ar)s=ars
③(ab)r=ar·br(b>0)
④ar÷as=ar-s
整数指数幂
分数指数幂
有理数指数幂
4.1 指数
4.1.2 无理指数幂及其运算性质
类比推广:实数指数幂
整数指数幂 分数指数幂
正数
负数
0
无理数指数幂
实数指数幂ax(a>0)
实数指数幂的运算性质(a>0 ; r,s∈R):
①ar·as=ar+s ②(ar)s=ars ③(ab)r=ar·br(b>0) ④ar÷as=ar-s
例题讲解
【例1】已知a+a-1=5,求下列各式的值:
a>1或0(a±b)2=a2±2ab+b2
2an·a-n=2
例题讲解
【变式】已知a+a-1=5(a>1),求下列各式的值:
a3+b3=(a+b)(a2-ab+b2)
a3 - b3=(a-b)(a2+ab+b2)
例题讲解P110
问题点拨
奇函数
奇函数
偶函数
非奇非偶函数
问题点拨
<
4.1 指数
4.1.1 n次方根与
分数指数幂
一、n次方根与根式
根式
根指数
被开方数
二、根式运算性质
口诀:开→方取本身,方→开论奇偶
巩固新知
x≤1
0
根式
分数指数幂
三、分数指数幂
①规定正数的正分数指数幂:
②规定正数的负分数指数幂:
③0的正分数指数幂为0;
0的负分数指数幂无意义.
三、分数指数幂
①规定正数的正分数指数幂:
②规定正数的负分数指数幂:
③0的正分数指数幂为0;0的负分数指数幂无意义.
(4)分数指数幂不可随意约分;
(5)有理数指数幂的运算性质(a>0 ; r,s∈Q):
①ar·as=ar+s ②(ar)s=ars ③(ab)r=ar·br(b>0) ④ar÷as=ar-s
整数指数幂
分数指数幂
有理数指数幂
四、有理指数幂
有理数指数幂的运算性质(a>0 ; r,s∈Q):
①ar·as=ar+s
②(ar)s=ars
③(ab)r=ar·br(b>0)
④ar÷as=ar-s
整数指数幂
分数指数幂
有理数指数幂
4.1 指数
4.1.2 无理指数幂及其运算性质
类比推广:实数指数幂
整数指数幂 分数指数幂
正数
负数
0
无理数指数幂
实数指数幂ax(a>0)
实数指数幂的运算性质(a>0 ; r,s∈R):
①ar·as=ar+s ②(ar)s=ars ③(ab)r=ar·br(b>0) ④ar÷as=ar-s
例题讲解
【例1】已知a+a-1=5,求下列各式的值:
a>1或0
2an·a-n=2
例题讲解
【变式】已知a+a-1=5(a>1),求下列各式的值:
a3+b3=(a+b)(a2-ab+b2)
a3 - b3=(a-b)(a2+ab+b2)
例题讲解P110
问题点拨
奇函数
奇函数
偶函数
非奇非偶函数
问题点拨
<
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
