北师大版九年级下册2.2二次函数的图象与性质 课件(共25张PPT)
文档属性
| 名称 | 北师大版九年级下册2.2二次函数的图象与性质 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-30 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
北师大版 九年级下册
二次函数的图象与性质
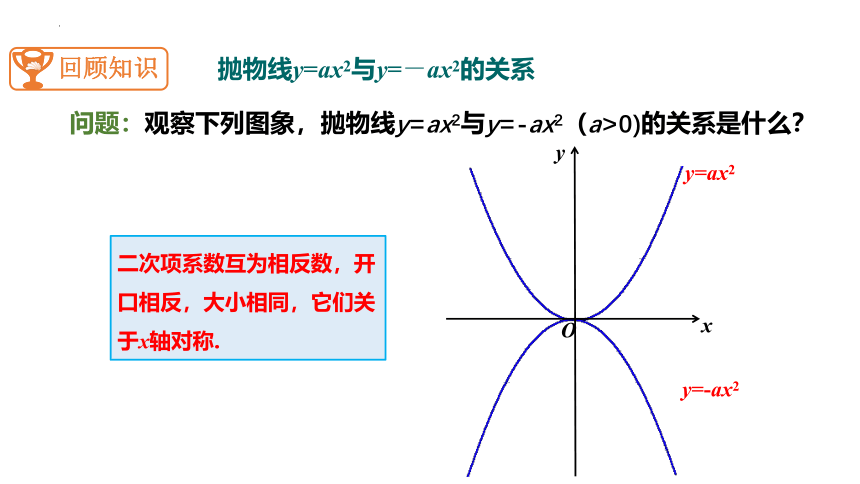
抛物线y=ax2与y=-ax2的关系
问题:观察下列图象,抛物线y=ax2与y=-ax2(a>0)的关系是什么?
二次项系数互为相反数,开口相反,大小相同,它们关于x轴对称.
x
y
O
y=ax2
y=-ax2
回顾知识
问题:形如y=2x2、y=x2、 y = x2、 y =- x2 、y=x2的二次函数的图象之间会存在什么关系呢?下面我们一起要探究它们之间的关系.
什么关系
思考问题
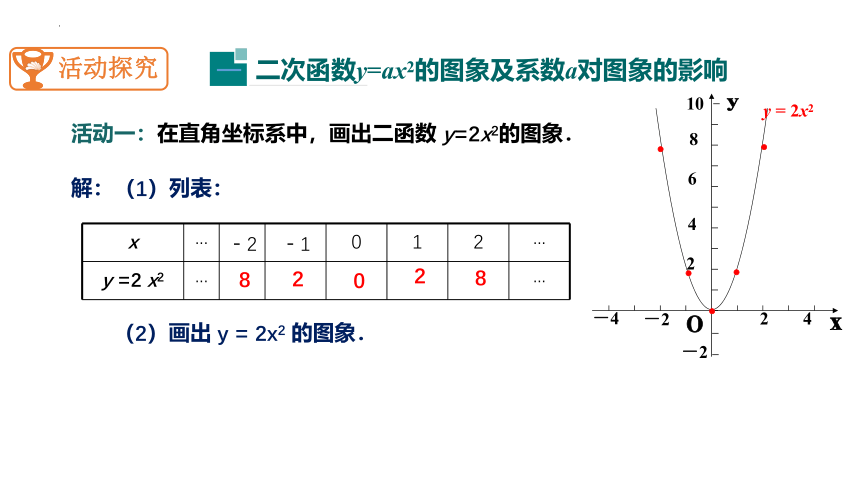
活动一:在直角坐标系中,画出二函数 y=2x2的图象.
解:(1)列表:
x ··· -2 -1 0 1 2 ···
y =2 x2 ··· ···
8
2
0
2
8
(2)画出 y = 2x2 的图象.
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2
二次函数y=ax2的图象及系数a对图象的影响
一
活动探究
问题:二次函数 y = 2x2 的图象是什么形状?它与二 次函数 y = x2 的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2
y = x2
①二次函数 y = 2x2 的图象:抛物线
②相同:形状相同、顶点(0,0)相同、开口都向上、 对称轴相同(y轴)
不同:开口大小不一样
活动探究
活动二:在图中画出 y = x2的图象,观察它与y = x2 、y = 2x2图象有什么相同和不同?
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2
y = x2
解:(1)列表:
x ··· -4 -2 0 2 4 ···
··· ···
8
0
8
(2)画出 y = x2 的图象.
y =x2
相同:形状相同、顶点(0,0)相同、开口都向上、对称轴相同(y轴)
不同:开口大小不一样
活动探究
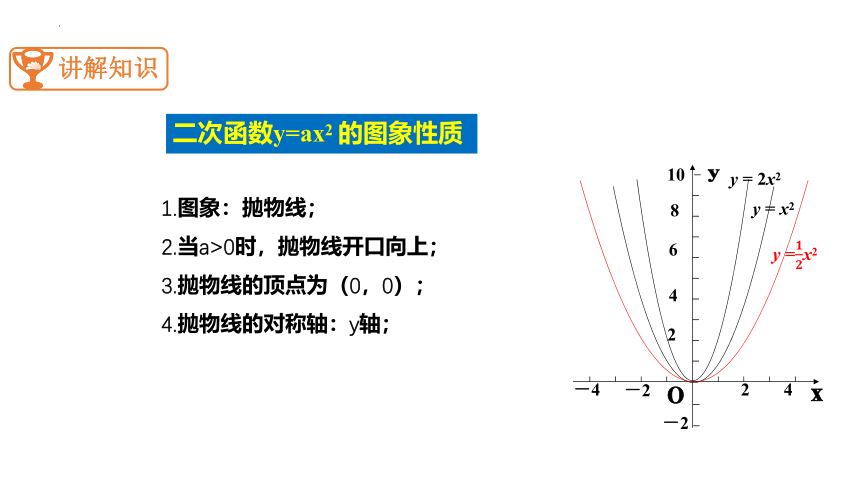
1.图象:抛物线;
2.当a>0时,抛物线开口向上;
3.抛物线的顶点为(0,0);
4.抛物线的对称轴:y轴;
二次函数y=ax2 的图象性质
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2
y = x2
y =x2
讲解知识
活动三:在图中画出 y =- x2、y = -x2 、y =-2x2图象有什么相同和不同?
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
-2
y = 2x2
y = x2
y =x2
结论:
1.二次函数y =- x2图象与 y = x2图象关于x轴对称;
2.对于二次函数y=ax :
①当a>0时,a的绝对值越大,开口越小.
②当a<0时,a的绝对值越大,开口越小.
y =x2
y =-x2
y =-2x2
例题讲解
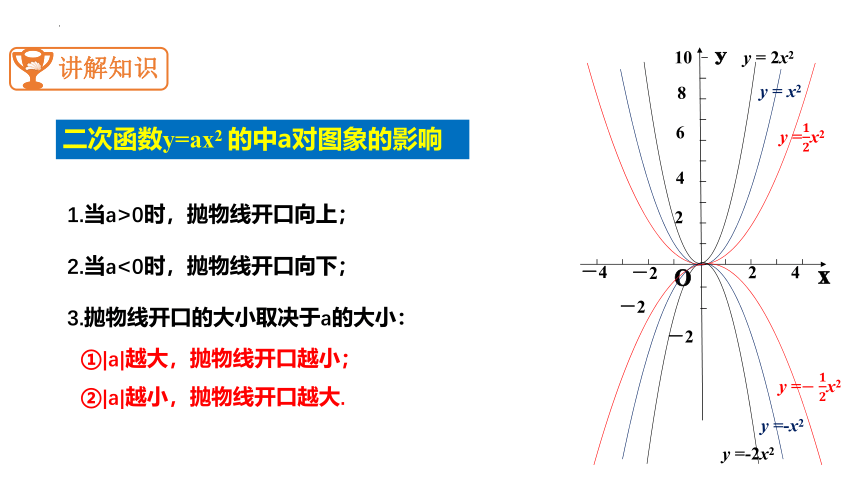
1.当a>0时,抛物线开口向上;
2.当a<0时,抛物线开口向下;
3.抛物线开口的大小取决于a的大小:
①|a|越大,抛物线开口越小;
②|a|越小,抛物线开口越大.
二次函数y=ax2 的中a对图象的影响
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
-2
y = 2x2
y = x2
y =x2
y =x2
y =-x2
y =-2x2
讲解知识
问题:形如y=ax2,y=ax2+c的二次函数的图象之间会存在什么关系呢?下面我们一起要探究它们之间的关系.
什么关系
思考问题
活动四:(1)画二次函数 y = 2x2+1 、 y =2x2-1的图象,你是怎样画的?与同伴进行交流.
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
解:先列表:
x ··· -2 -1.5 -1 0 1 1.5 2 ···
y =2x2+1 ··· ···
y = 2x2-1 ··· ···
9
5.5
3
1
3
5.5
9
7
3.5
1
-1
1
3.5
7
二次函数y=ax2+c的图象及平移
三
y = 2x2呢?
活动探究
(2)抛物线y =2 x2,y=2x2+1,y=2x2-1的开口方向、对称轴和顶点各是什么?
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
y =2 x2 向上 (0,0) y轴
y =2 x2+1
y = 2x2-1
二次函数
开口方向
顶点坐标
对称轴
向上
向上
(0,1)
(0,-1)
y轴
y轴
活动探究
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
(3) 抛物线 y=2x2+1,y=2x2-1与抛物线y=2x2 有什么关系?
可以发现,把抛物线y=2x2 向 平移1个单位长度,就得到抛物线 ;把抛物线 y=2x2 向 平移1个单位长度,就得到抛物线 y=2x2-1.
抛物线 y=2x2+1的顶点坐标为:(0,1)
抛物线 y=2x2-1的顶点坐标为:(0,-1)
抛物线 y=2x2的顶点坐标为:(0,0)
下
y=2x2+1
上
活动探究
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
二次函数y=2x2,y =2x2 + 1,y=2x2 - 1 的图象都是抛物线,并且形状相同,只是顶点不同,位置不同.
将二次函数 y =2x2的图象向上平移 1 个单位,就得到 函数 y = 2x2+ 1 的图象;
将二次函数 y = 2x2的图象向下平移 1 个单位,就得 到函数 y = 2x2 - 1 的图象.
二次函数y=ax2+c的图象及平移
三
活动结果
二次函数y=ax2+c的图象可以由 y=ax2 的图象平移得到:
当c > 0 时,向上平移c个单位长度得到.
当c < 0 时,向下平移-c个单位长度得到.
二次函数y=ax2 与y=ax2+c(a ≠ 0)的图象的关系
上下平移规律:
平方项不变,常数项上加下减.
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = ax2+c
y = ax2-c
c决定顶点的纵坐标.
讲解知识
【例1】把抛物线y = 2x2向上平移5个单位,会得到哪条抛物线?向下平移2个单位呢?
x
y
O
-2
2
2
4
6
4
-4
8
-2
-4
例题讲解
【例2】在图中画出 y =- x2、y =-2x2的图象.
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
-2
y =x2
y =-2x2
例题讲解
函数 开口方向 对称轴 顶点坐标 两者关系
y=ax2 当a>0时,向上 当a<0时,向下 y轴 (0,0) 当c>0时,y=ax2图象向上平移c个单位长度得到y=ax2+c的图象;
当c<0时,y=ax2图象向下平移|c|个单位长度得到y=ax2+c的图象;
y=ax2+c 当a>0时,向上 当a<0时,向下 y轴 (0,c)
二次函数y=ax2+c(a ≠ 0)的特点
知识小结
1、抛物线y=2x2向下平移4个单位,就得到抛物线 .
2、填表:
y = 2x2-4
函数 开口方向 顶点 对称轴 有最高(低)点
y = 3x2
y = 3x2+1
y = -4x2-5
向上
向上
向下
(0,0)
(0,1)
(0,-5)
y轴
y轴
y轴
有最低点
有最低点
有最高点
课堂练习
3.已知(m,n)在y=ax2+a(a不为0)的图象上,(-m,n) ___(填“在”或“不在”)y=ax2+a(a不为0)的图象上.
4. 若y=x2+(k-2)的顶点是原点,则k____;若顶点位于x轴上方,则k____;若顶点位于x轴下方,则k .
在
=2
>2
<2
课堂练习
5.不画函数y=-x2和y=-x2+1的图象回答下面的问题:
(1)抛物线y=-x2+1经过怎样的平移才能得到抛物线y=-x2.
(2)函数y=-x2+1,当x 时, y随x的增大而减小;当x 时,函数y有最大值,最大值y是 ,其图象与y轴的交点坐标是 .
(3)试说出抛物线y=x2-3的开口方向、对称轴和顶点坐标.
向下平移1个单位.
>0
=0
1
(0,1)
开口方向向上,对称轴是y轴,顶点坐标(0,-3).
课堂练习
(2019 嘉定区)将抛物线y=x2﹣2x﹣1向上平移1个单位,平移后所得抛物线的表达式是( )
A.y=x2﹣2x
B.y=x2﹣2x﹣2
C.y=x2﹣x﹣1
D.y=x2﹣3x﹣1
A
解:∵将抛物线y=x2﹣2x﹣1向上平移1个单位,
∴平移后抛物线的表达式y=x2﹣2x﹣1+1,
即y=x2﹣2x.
故选:A.
中考链接
二次函数y=ax2+c(a≠0)的图象和性质
图象
性质
与y=ax2的关系
开口方向由a的符号决定;
c决定顶点位置;
对称轴是y轴.
增减性结合开口方向和对称轴才能确定.
平移规律:
k正向上;
k负向下.
课堂总结
作业布置
教材第36页习题2.3第1、2、3题.
谢谢观看!
北师大版 九年级下册
二次函数的图象与性质
抛物线y=ax2与y=-ax2的关系
问题:观察下列图象,抛物线y=ax2与y=-ax2(a>0)的关系是什么?
二次项系数互为相反数,开口相反,大小相同,它们关于x轴对称.
x
y
O
y=ax2
y=-ax2
回顾知识
问题:形如y=2x2、y=x2、 y = x2、 y =- x2 、y=x2的二次函数的图象之间会存在什么关系呢?下面我们一起要探究它们之间的关系.
什么关系
思考问题
活动一:在直角坐标系中,画出二函数 y=2x2的图象.
解:(1)列表:
x ··· -2 -1 0 1 2 ···
y =2 x2 ··· ···
8
2
0
2
8
(2)画出 y = 2x2 的图象.
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2
二次函数y=ax2的图象及系数a对图象的影响
一
活动探究
问题:二次函数 y = 2x2 的图象是什么形状?它与二 次函数 y = x2 的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2
y = x2
①二次函数 y = 2x2 的图象:抛物线
②相同:形状相同、顶点(0,0)相同、开口都向上、 对称轴相同(y轴)
不同:开口大小不一样
活动探究
活动二:在图中画出 y = x2的图象,观察它与y = x2 、y = 2x2图象有什么相同和不同?
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2
y = x2
解:(1)列表:
x ··· -4 -2 0 2 4 ···
··· ···
8
0
8
(2)画出 y = x2 的图象.
y =x2
相同:形状相同、顶点(0,0)相同、开口都向上、对称轴相同(y轴)
不同:开口大小不一样
活动探究
1.图象:抛物线;
2.当a>0时,抛物线开口向上;
3.抛物线的顶点为(0,0);
4.抛物线的对称轴:y轴;
二次函数y=ax2 的图象性质
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2
y = x2
y =x2
讲解知识
活动三:在图中画出 y =- x2、y = -x2 、y =-2x2图象有什么相同和不同?
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
-2
y = 2x2
y = x2
y =x2
结论:
1.二次函数y =- x2图象与 y = x2图象关于x轴对称;
2.对于二次函数y=ax :
①当a>0时,a的绝对值越大,开口越小.
②当a<0时,a的绝对值越大,开口越小.
y =x2
y =-x2
y =-2x2
例题讲解
1.当a>0时,抛物线开口向上;
2.当a<0时,抛物线开口向下;
3.抛物线开口的大小取决于a的大小:
①|a|越大,抛物线开口越小;
②|a|越小,抛物线开口越大.
二次函数y=ax2 的中a对图象的影响
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
-2
y = 2x2
y = x2
y =x2
y =x2
y =-x2
y =-2x2
讲解知识
问题:形如y=ax2,y=ax2+c的二次函数的图象之间会存在什么关系呢?下面我们一起要探究它们之间的关系.
什么关系
思考问题
活动四:(1)画二次函数 y = 2x2+1 、 y =2x2-1的图象,你是怎样画的?与同伴进行交流.
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
解:先列表:
x ··· -2 -1.5 -1 0 1 1.5 2 ···
y =2x2+1 ··· ···
y = 2x2-1 ··· ···
9
5.5
3
1
3
5.5
9
7
3.5
1
-1
1
3.5
7
二次函数y=ax2+c的图象及平移
三
y = 2x2呢?
活动探究
(2)抛物线y =2 x2,y=2x2+1,y=2x2-1的开口方向、对称轴和顶点各是什么?
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
y =2 x2 向上 (0,0) y轴
y =2 x2+1
y = 2x2-1
二次函数
开口方向
顶点坐标
对称轴
向上
向上
(0,1)
(0,-1)
y轴
y轴
活动探究
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
(3) 抛物线 y=2x2+1,y=2x2-1与抛物线y=2x2 有什么关系?
可以发现,把抛物线y=2x2 向 平移1个单位长度,就得到抛物线 ;把抛物线 y=2x2 向 平移1个单位长度,就得到抛物线 y=2x2-1.
抛物线 y=2x2+1的顶点坐标为:(0,1)
抛物线 y=2x2-1的顶点坐标为:(0,-1)
抛物线 y=2x2的顶点坐标为:(0,0)
下
y=2x2+1
上
活动探究
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = 2x2+1
y = 2x2-1
二次函数y=2x2,y =2x2 + 1,y=2x2 - 1 的图象都是抛物线,并且形状相同,只是顶点不同,位置不同.
将二次函数 y =2x2的图象向上平移 1 个单位,就得到 函数 y = 2x2+ 1 的图象;
将二次函数 y = 2x2的图象向下平移 1 个单位,就得 到函数 y = 2x2 - 1 的图象.
二次函数y=ax2+c的图象及平移
三
活动结果
二次函数y=ax2+c的图象可以由 y=ax2 的图象平移得到:
当c > 0 时,向上平移c个单位长度得到.
当c < 0 时,向下平移-c个单位长度得到.
二次函数y=ax2 与y=ax2+c(a ≠ 0)的图象的关系
上下平移规律:
平方项不变,常数项上加下减.
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y = ax2+c
y = ax2-c
c决定顶点的纵坐标.
讲解知识
【例1】把抛物线y = 2x2向上平移5个单位,会得到哪条抛物线?向下平移2个单位呢?
x
y
O
-2
2
2
4
6
4
-4
8
-2
-4
例题讲解
【例2】在图中画出 y =- x2、y =-2x2的图象.
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
-2
y =x2
y =-2x2
例题讲解
函数 开口方向 对称轴 顶点坐标 两者关系
y=ax2 当a>0时,向上 当a<0时,向下 y轴 (0,0) 当c>0时,y=ax2图象向上平移c个单位长度得到y=ax2+c的图象;
当c<0时,y=ax2图象向下平移|c|个单位长度得到y=ax2+c的图象;
y=ax2+c 当a>0时,向上 当a<0时,向下 y轴 (0,c)
二次函数y=ax2+c(a ≠ 0)的特点
知识小结
1、抛物线y=2x2向下平移4个单位,就得到抛物线 .
2、填表:
y = 2x2-4
函数 开口方向 顶点 对称轴 有最高(低)点
y = 3x2
y = 3x2+1
y = -4x2-5
向上
向上
向下
(0,0)
(0,1)
(0,-5)
y轴
y轴
y轴
有最低点
有最低点
有最高点
课堂练习
3.已知(m,n)在y=ax2+a(a不为0)的图象上,(-m,n) ___(填“在”或“不在”)y=ax2+a(a不为0)的图象上.
4. 若y=x2+(k-2)的顶点是原点,则k____;若顶点位于x轴上方,则k____;若顶点位于x轴下方,则k .
在
=2
>2
<2
课堂练习
5.不画函数y=-x2和y=-x2+1的图象回答下面的问题:
(1)抛物线y=-x2+1经过怎样的平移才能得到抛物线y=-x2.
(2)函数y=-x2+1,当x 时, y随x的增大而减小;当x 时,函数y有最大值,最大值y是 ,其图象与y轴的交点坐标是 .
(3)试说出抛物线y=x2-3的开口方向、对称轴和顶点坐标.
向下平移1个单位.
>0
=0
1
(0,1)
开口方向向上,对称轴是y轴,顶点坐标(0,-3).
课堂练习
(2019 嘉定区)将抛物线y=x2﹣2x﹣1向上平移1个单位,平移后所得抛物线的表达式是( )
A.y=x2﹣2x
B.y=x2﹣2x﹣2
C.y=x2﹣x﹣1
D.y=x2﹣3x﹣1
A
解:∵将抛物线y=x2﹣2x﹣1向上平移1个单位,
∴平移后抛物线的表达式y=x2﹣2x﹣1+1,
即y=x2﹣2x.
故选:A.
中考链接
二次函数y=ax2+c(a≠0)的图象和性质
图象
性质
与y=ax2的关系
开口方向由a的符号决定;
c决定顶点位置;
对称轴是y轴.
增减性结合开口方向和对称轴才能确定.
平移规律:
k正向上;
k负向下.
课堂总结
作业布置
教材第36页习题2.3第1、2、3题.
谢谢观看!
