2021-2022学年北师大版九年级数学下册1.4 解直角三角形 课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册1.4 解直角三角形 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-30 13:21:47 | ||
图片预览





文档简介
(共19张PPT)
北师大版 九年级下册
解直角三角形
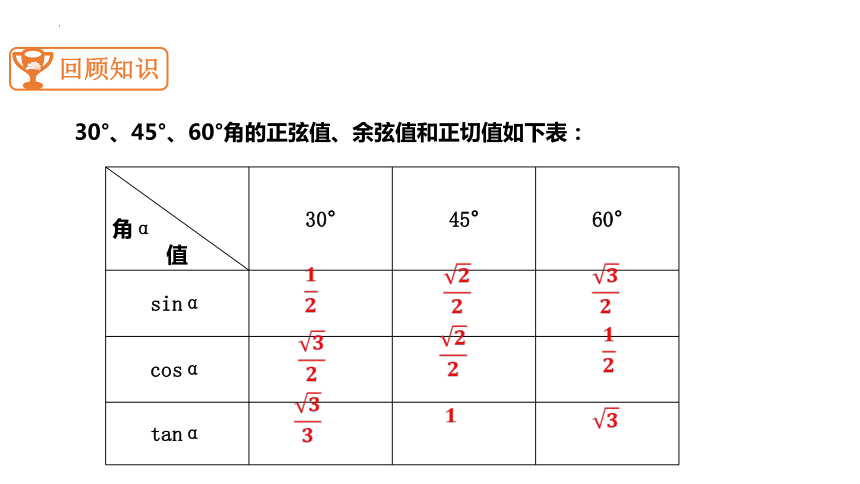
角α 值 30° 45° 60°
sinα
cosα
tanα
30°、45°、60°角的正弦值、余弦值和正切值如下表:
回顾知识
A
C
B
c
b
a
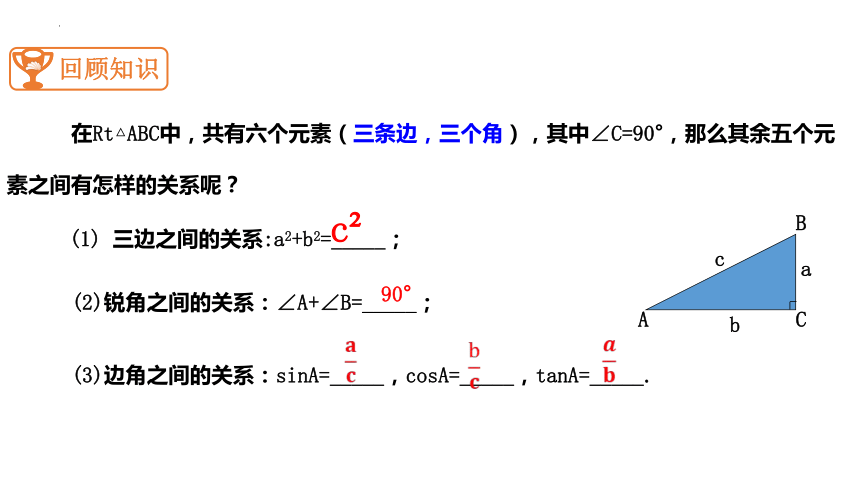
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
90°
c
回顾知识
在一个直角三角形中,除直角外有5个元素(3条边、2个锐角),要至少知道其中的几个元素就可以求出其余的元素?
如果知道的2个元素都是角,不能求解.因为此时的直角三角形有无数多个.
如果已知2个元素,且至少有一个元素是边就可以了.
新课讲解
在直角三角形ABC中,如果已知其中两边的长,你能求出这个三角形的其他元素吗?
【例1】如图,在Rt△ABC中,∠C=90°,a=b=求这个直角三角形的其他元素.
解:在Rt△ABC中,a2+b2=c2, a=b=
∴c=2.
在Rt△ABC中,sinB=
∴ ∠ B = 30° ,∠ A = 60°
A
B
C
如果已知直角三角形两边的长度,可以求出其他元素.
新课讲解
在直角三角形ABC中,如果已知一边和一个锐角,你能求出这个三角形的其他元素吗?
【例2】在 Rt△ABC 中,∠ C 为直角,∠ A,∠ B,∠ C 所对的边分别为 a, b,c,且 b = 30,∠ B=25° ,求这个三角形的其他元素(边长精确到1).
解:在 Rt△ABC 中,∠ C = 90° ,∠ B = 25°,
∴ ∠ A = 65
∵ sin B =,b = 30, ∴ c = = ≈ 71.
∵ tan B = ,b = 30, ∴ a = = ≈ 64.
如果已知直角三角形的一边和一个锐角,可以求出其他元素.
新课讲解
在直角三角形的6个元素(即3条边和3个锐角)中,直角是已知元素,如果再知道一条边和第三个元素,这个三角形的所有元素就可以确定下来
新课讲解
解直角三角形的依据:
(1)三边之间的关系:a2+b2=c2(勾股定理);
(2)锐角之间的关系:∠A+∠B= 90°;
(3)边角之间的关系:sin A=cos A=
(4)面积公式:S△ABC=
在直角三角形中,由直角三角形中已知元素,求出所有未知元素的过程,叫做解直角三角形.
新课讲解
【例3】如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tan A=,
求sin B+cos B的值.
解:在Rt△ACD中,∵∠ADC=90°,
∴tan A===32,∴AD=4,∴BD=AB-AD=12-4=8.
在Rt△BCD中,∵∠BDC=90°,BD=8,CD=6,
∴BC==10,
∴sin B==35,cos B==,∴sin B+cos B=+=.
新课讲解
1.做标注:在遇到解直角三形的问题时,先画一个直角三角形的草图,按题意标明 哪些元素是已知的,哪些元素是未知的,以得于分析解决问题.
2.找关系式:选取关系式时要尽量利用原始数据,以防止“累积错误”.
3.遵循规则:遵循“有斜用弦,无斜用切;宁乘勿除,化斜为直”.
说说解直角三角形时,有哪些注意点?
新课讲解
1.如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别记作a,b,c.
(1)直角三角形的三边之间的关系为________________;
(2)直角三角形的两个锐角之间的关系为__________________;
(3)直角三角形的边和锐角之间的关系为sin A=_____,
cos A=_____,tan A=_____,tan B=_____.
a2+b2=c2(勾股定理)
∠A+∠B=90°
课堂练习
2.在Rt△ABC中,∠C=90°,BC=,AC=,则∠A的度数为( )
A.90° B.60° C.45° D.30°
3.在Rt△ABC中,∠C=90°,AC=3,BC=4,则cos A的值是( )
A. B. C. D.
D
A
课堂练习
4.如图,在Rt△ABC中,∠B=90°,∠A=30°,a=5,求∠B,b,c.
解:∵∠B=90°-∠A=60° ,∠A=30°.且tan B=.
∴b=a·tan B=5·tan60°=5
∵sin A=
∴= 10.
课堂练习
5.如图,在Rt△ABC中,∠C=90°,cos A = ,BC = 5, 试求AB的长.
解:∵ ∠C=90° ,cos A = ,∴
设AB=x,则AC=
又AB =AC +BC ,则x =(x) +5
∴x1=,x2=(舍去)
∴AB的长为.
课堂练习
(2018·上海)如图,已知△ABC中,AB=BC=5,tan∠ABC.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
解:(1)作A作AE⊥BC.
在Rt△ABE中,tan∠ABC,AB=5,
∴AE=3,BE=4,
E
中考链接
(2018·上海)如图,已知△ABC中,AB=BC=5,tan∠ABC.
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
解:∵DF垂直平分BC,
∴BD=CD,BF=CF,
∵tan∠DBF,
∴DF,
在Rt△BFD中,根据勾股定理得:BD,
∴AD=5,则.
中考链接
解直角三角形
2.依据:
(1)三边之间的关系:a2+b2=c2(勾股定理);
(2)锐角之间的关系:∠A+∠B= 90°;
(3)边角之间的关系:sin A=cos A=
(4)面积公式:S△ABC=
1.概念:在直角三角形中,由直角三角形中已知元素,求出所有未知元素的过程,叫做解直角三角形.
课堂总结
作业布置
教材第17页习题1.5第1、2题.
教材第18页习题1.5第3、4题.
谢谢观看!
北师大版 九年级下册
解直角三角形
角α 值 30° 45° 60°
sinα
cosα
tanα
30°、45°、60°角的正弦值、余弦值和正切值如下表:
回顾知识
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:sinA=_____,cosA=_____,tanA=_____.
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
90°
c
回顾知识
在一个直角三角形中,除直角外有5个元素(3条边、2个锐角),要至少知道其中的几个元素就可以求出其余的元素?
如果知道的2个元素都是角,不能求解.因为此时的直角三角形有无数多个.
如果已知2个元素,且至少有一个元素是边就可以了.
新课讲解
在直角三角形ABC中,如果已知其中两边的长,你能求出这个三角形的其他元素吗?
【例1】如图,在Rt△ABC中,∠C=90°,a=b=求这个直角三角形的其他元素.
解:在Rt△ABC中,a2+b2=c2, a=b=
∴c=2.
在Rt△ABC中,sinB=
∴ ∠ B = 30° ,∠ A = 60°
A
B
C
如果已知直角三角形两边的长度,可以求出其他元素.
新课讲解
在直角三角形ABC中,如果已知一边和一个锐角,你能求出这个三角形的其他元素吗?
【例2】在 Rt△ABC 中,∠ C 为直角,∠ A,∠ B,∠ C 所对的边分别为 a, b,c,且 b = 30,∠ B=25° ,求这个三角形的其他元素(边长精确到1).
解:在 Rt△ABC 中,∠ C = 90° ,∠ B = 25°,
∴ ∠ A = 65
∵ sin B =,b = 30, ∴ c = = ≈ 71.
∵ tan B = ,b = 30, ∴ a = = ≈ 64.
如果已知直角三角形的一边和一个锐角,可以求出其他元素.
新课讲解
在直角三角形的6个元素(即3条边和3个锐角)中,直角是已知元素,如果再知道一条边和第三个元素,这个三角形的所有元素就可以确定下来
新课讲解
解直角三角形的依据:
(1)三边之间的关系:a2+b2=c2(勾股定理);
(2)锐角之间的关系:∠A+∠B= 90°;
(3)边角之间的关系:sin A=cos A=
(4)面积公式:S△ABC=
在直角三角形中,由直角三角形中已知元素,求出所有未知元素的过程,叫做解直角三角形.
新课讲解
【例3】如图,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tan A=,
求sin B+cos B的值.
解:在Rt△ACD中,∵∠ADC=90°,
∴tan A===32,∴AD=4,∴BD=AB-AD=12-4=8.
在Rt△BCD中,∵∠BDC=90°,BD=8,CD=6,
∴BC==10,
∴sin B==35,cos B==,∴sin B+cos B=+=.
新课讲解
1.做标注:在遇到解直角三形的问题时,先画一个直角三角形的草图,按题意标明 哪些元素是已知的,哪些元素是未知的,以得于分析解决问题.
2.找关系式:选取关系式时要尽量利用原始数据,以防止“累积错误”.
3.遵循规则:遵循“有斜用弦,无斜用切;宁乘勿除,化斜为直”.
说说解直角三角形时,有哪些注意点?
新课讲解
1.如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别记作a,b,c.
(1)直角三角形的三边之间的关系为________________;
(2)直角三角形的两个锐角之间的关系为__________________;
(3)直角三角形的边和锐角之间的关系为sin A=_____,
cos A=_____,tan A=_____,tan B=_____.
a2+b2=c2(勾股定理)
∠A+∠B=90°
课堂练习
2.在Rt△ABC中,∠C=90°,BC=,AC=,则∠A的度数为( )
A.90° B.60° C.45° D.30°
3.在Rt△ABC中,∠C=90°,AC=3,BC=4,则cos A的值是( )
A. B. C. D.
D
A
课堂练习
4.如图,在Rt△ABC中,∠B=90°,∠A=30°,a=5,求∠B,b,c.
解:∵∠B=90°-∠A=60° ,∠A=30°.且tan B=.
∴b=a·tan B=5·tan60°=5
∵sin A=
∴= 10.
课堂练习
5.如图,在Rt△ABC中,∠C=90°,cos A = ,BC = 5, 试求AB的长.
解:∵ ∠C=90° ,cos A = ,∴
设AB=x,则AC=
又AB =AC +BC ,则x =(x) +5
∴x1=,x2=(舍去)
∴AB的长为.
课堂练习
(2018·上海)如图,已知△ABC中,AB=BC=5,tan∠ABC.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
解:(1)作A作AE⊥BC.
在Rt△ABE中,tan∠ABC,AB=5,
∴AE=3,BE=4,
E
中考链接
(2018·上海)如图,已知△ABC中,AB=BC=5,tan∠ABC.
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
解:∵DF垂直平分BC,
∴BD=CD,BF=CF,
∵tan∠DBF,
∴DF,
在Rt△BFD中,根据勾股定理得:BD,
∴AD=5,则.
中考链接
解直角三角形
2.依据:
(1)三边之间的关系:a2+b2=c2(勾股定理);
(2)锐角之间的关系:∠A+∠B= 90°;
(3)边角之间的关系:sin A=cos A=
(4)面积公式:S△ABC=
1.概念:在直角三角形中,由直角三角形中已知元素,求出所有未知元素的过程,叫做解直角三角形.
课堂总结
作业布置
教材第17页习题1.5第1、2题.
教材第18页习题1.5第3、4题.
谢谢观看!
