人教版数学八年级上册课课练:13.1.1轴对称(Word版含答案)
文档属性
| 名称 | 人教版数学八年级上册课课练:13.1.1轴对称(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 227.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-30 16:18:20 | ||
图片预览

文档简介
[轴对称]
一、选择题
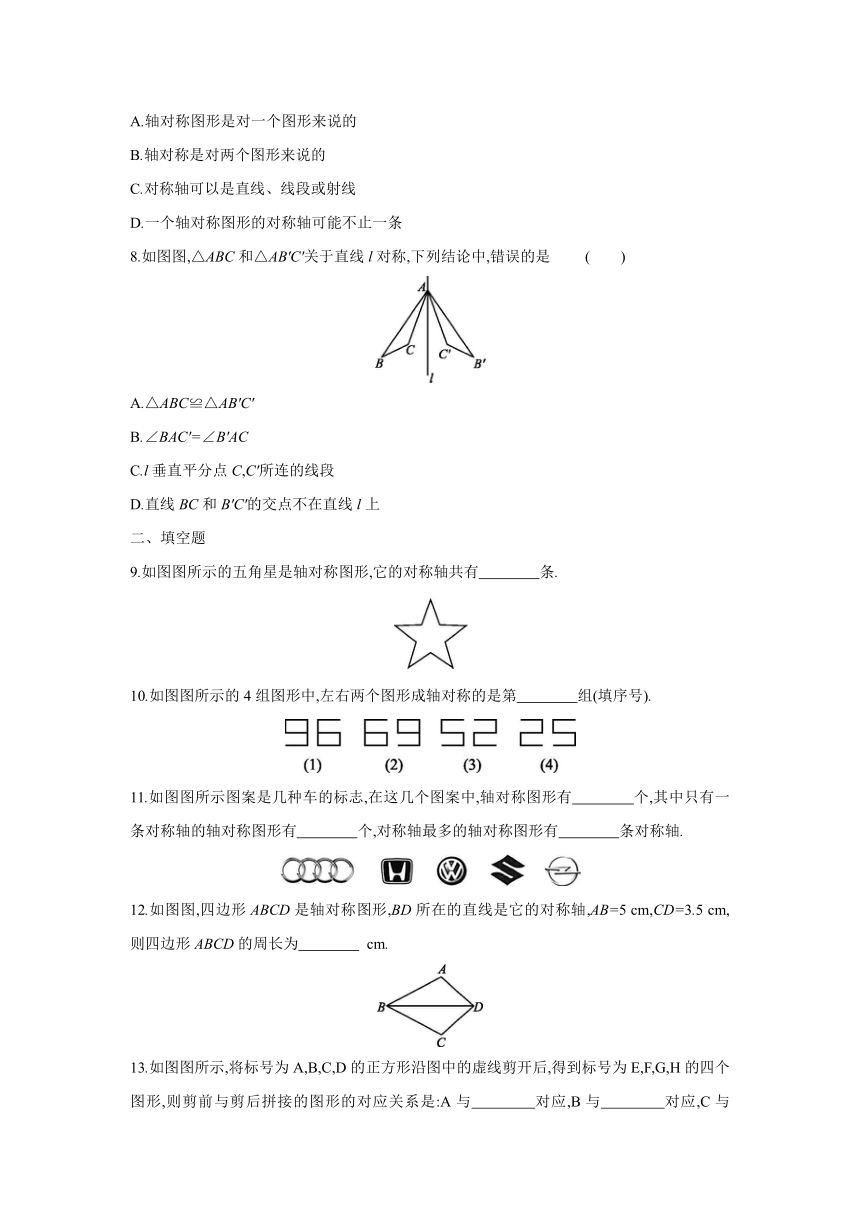
1.下列倡导节约的图案中,属于轴对称图形的是( )
2.在3×3的正方形网格中,每个小正方形都是全等的,其中有3个小正方形被涂上了阴影,下列所组成的图形中,不是轴对称图形的是 ( )
3.下列轴对称图形中,只有一条对称轴的是 ( )
4.角是轴对称图形,它的对称轴是 ( )
A.这个角的平分线
B.这个角的其中一条边所在的直线
C.这个角的其中一条边的垂线
D.这个角的平分线所在的直线
5.如图图,线段AB与A'B'(AB=A'B')不关于直线l成轴对称的是 ( )
6.如图图,△ABC与△DEF关于直线l对称,若∠A=65°,∠B=80°,则∠F等于 ( )
A.80° B.65° C.45° D.35°
7.关于轴对称和轴对称图形,下列说法错误的是 ( )
A.轴对称图形是对一个图形来说的
B.轴对称是对两个图形来说的
C.对称轴可以是直线、线段或射线
D.一个轴对称图形的对称轴可能不止一条
8.如图图,△ABC和△AB'C'关于直线l对称,下列结论中,错误的是 ( )
A.△ABC≌△AB'C'
B.∠BAC'=∠B'AC
C.l垂直平分点C,C'所连的线段
D.直线BC和B'C'的交点不在直线l上
二、填空题
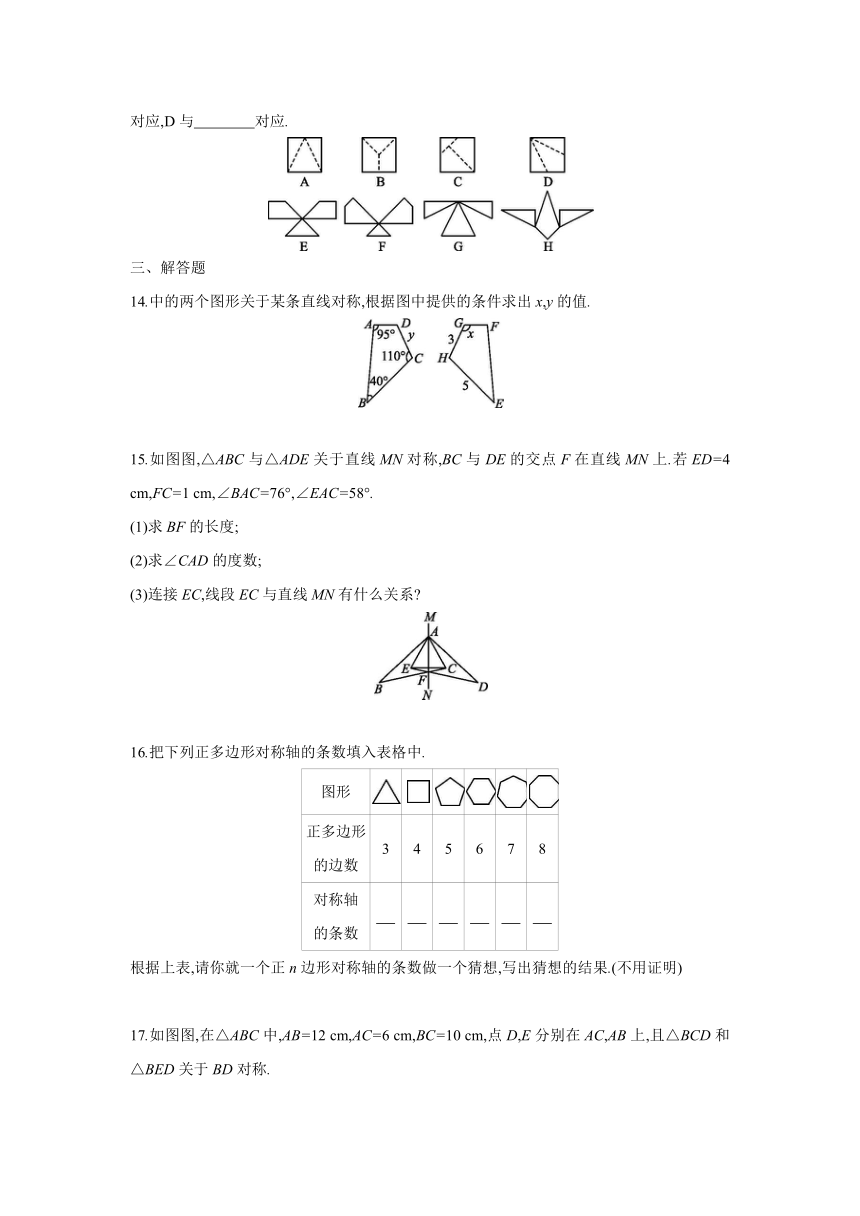
9.如图图所示的五角星是轴对称图形,它的对称轴共有 条.
10.如图图所示的4组图形中,左右两个图形成轴对称的是第 组(填序号).
11.如图图所示图案是几种车的标志,在这几个图案中,轴对称图形有 个,其中只有一条对称轴的轴对称图形有 个,对称轴最多的轴对称图形有 条对称轴.
12.如图图,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=5 cm,CD=3.5 cm,则四边形ABCD的周长为 cm.
13.如图图所示,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为E,F,G,H的四个图形,则剪前与剪后拼接的图形的对应关系是:A与 对应,B与 对应,C与 对应,D与 对应.
三、解答题
14.中的两个图形关于某条直线对称,根据图中提供的条件求出x,y的值.
15.如图图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4 cm,FC=1 cm,∠BAC=76°,∠EAC=58°.
(1)求BF的长度;
(2)求∠CAD的度数;
(3)连接EC,线段EC与直线MN有什么关系
16.把下列正多边形对称轴的条数填入表格中.
图形
正多边形 的边数 3 4 5 6 7 8
对称轴 的条数
根据上表,请你就一个正n边形对称轴的条数做一个猜想,写出猜想的结果.(不用证明)
17.如图图,在△ABC中,AB=12 cm,AC=6 cm,BC=10 cm,点D,E分别在AC,AB上,且△BCD和△BED关于BD对称.
(1)求AE的长;
(2)求△ADE的周长.
如图图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
答案
1.B 2.C 3.B 4.D
5.A 6.D 7.C 8.D
9.5 如图图图,五角星的对称轴共有5条.
10.(3)(4) 11.3 2 2 12.17
13.G E F H A剪开后是三个三角形,B剪开后是两个直角梯形和一个三角形,C剪开后是一个直角三角形和两个四边形,D剪开后是两个三角形和一个四边形,因而,A与G对应,B与E对应,C与F对应,D与H对应.
14. 因为两个图形关于某条直线对称,所以观察发现A和F,B和E,C和H,D和G分别是对称点,因此CD边与HG边是对应边,长度相等,∠ADC和∠FGH是对应角,大小相等.
解:x=∠ADC=360°-40°-95°-110°=115°,y=HG=3.
15.解:(1)∵△ABC与△ADE关于直线MN对称,ED=4 cm,
∴BC=ED=4 cm.
又∵FC=1 cm,
∴BF=BC-FC=3 cm.
(2)∵△ABC与△ADE关于直线MN对称,∠BAC=76°,
∴∠EAD=∠BAC=76°.
又∵∠EAC=58°,∴∠CAD=∠EAD-∠EAC=76°-58°=18°.
(3)直线MN垂直平分线段EC.
理由如图图下:∵点E,C关于直线MN对称,
∴直线MN垂直平分线段EC.
16.解:3 4 5 6 7 8
猜想:一个正n边形有n条对称轴.
17.解:(1)∵△BCD和△BED关于BD对称,
∴△BCD≌△BED.
∴BE=BC=10 cm.
∴AE=AB-BE=12-10=2(cm).
(2)∵△BCD≌△BED,∴DC=DE.
∴△ADE的周长=AE+AD+DE=AE+AC=8 cm.
[素养提升]
解:(1)证明:在长方形ABCD中,DA=BC,∠A=∠D=∠B=∠BCD=90°.
由折叠的性质,得GC=DA,∠G=∠D=90°,∠GCE=∠A=90°.
∴GC=BC,∠GCF+∠FCE=90°.
又∵∠FCE+∠BCE=90°,
∴∠GCF=∠BCE.
又∵∠G=∠B=90°,GC=BC,
∴△FGC≌△EBC(ASA).
(2)由(1)知,DF=GF=BE,
∴S四边形ECGF=S四边形AEFD=====16.
一、选择题
1.下列倡导节约的图案中,属于轴对称图形的是( )
2.在3×3的正方形网格中,每个小正方形都是全等的,其中有3个小正方形被涂上了阴影,下列所组成的图形中,不是轴对称图形的是 ( )
3.下列轴对称图形中,只有一条对称轴的是 ( )
4.角是轴对称图形,它的对称轴是 ( )
A.这个角的平分线
B.这个角的其中一条边所在的直线
C.这个角的其中一条边的垂线
D.这个角的平分线所在的直线
5.如图图,线段AB与A'B'(AB=A'B')不关于直线l成轴对称的是 ( )
6.如图图,△ABC与△DEF关于直线l对称,若∠A=65°,∠B=80°,则∠F等于 ( )
A.80° B.65° C.45° D.35°
7.关于轴对称和轴对称图形,下列说法错误的是 ( )
A.轴对称图形是对一个图形来说的
B.轴对称是对两个图形来说的
C.对称轴可以是直线、线段或射线
D.一个轴对称图形的对称轴可能不止一条
8.如图图,△ABC和△AB'C'关于直线l对称,下列结论中,错误的是 ( )
A.△ABC≌△AB'C'
B.∠BAC'=∠B'AC
C.l垂直平分点C,C'所连的线段
D.直线BC和B'C'的交点不在直线l上
二、填空题
9.如图图所示的五角星是轴对称图形,它的对称轴共有 条.
10.如图图所示的4组图形中,左右两个图形成轴对称的是第 组(填序号).
11.如图图所示图案是几种车的标志,在这几个图案中,轴对称图形有 个,其中只有一条对称轴的轴对称图形有 个,对称轴最多的轴对称图形有 条对称轴.
12.如图图,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=5 cm,CD=3.5 cm,则四边形ABCD的周长为 cm.
13.如图图所示,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为E,F,G,H的四个图形,则剪前与剪后拼接的图形的对应关系是:A与 对应,B与 对应,C与 对应,D与 对应.
三、解答题
14.中的两个图形关于某条直线对称,根据图中提供的条件求出x,y的值.
15.如图图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4 cm,FC=1 cm,∠BAC=76°,∠EAC=58°.
(1)求BF的长度;
(2)求∠CAD的度数;
(3)连接EC,线段EC与直线MN有什么关系
16.把下列正多边形对称轴的条数填入表格中.
图形
正多边形 的边数 3 4 5 6 7 8
对称轴 的条数
根据上表,请你就一个正n边形对称轴的条数做一个猜想,写出猜想的结果.(不用证明)
17.如图图,在△ABC中,AB=12 cm,AC=6 cm,BC=10 cm,点D,E分别在AC,AB上,且△BCD和△BED关于BD对称.
(1)求AE的长;
(2)求△ADE的周长.
如图图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
答案
1.B 2.C 3.B 4.D
5.A 6.D 7.C 8.D
9.5 如图图图,五角星的对称轴共有5条.
10.(3)(4) 11.3 2 2 12.17
13.G E F H A剪开后是三个三角形,B剪开后是两个直角梯形和一个三角形,C剪开后是一个直角三角形和两个四边形,D剪开后是两个三角形和一个四边形,因而,A与G对应,B与E对应,C与F对应,D与H对应.
14. 因为两个图形关于某条直线对称,所以观察发现A和F,B和E,C和H,D和G分别是对称点,因此CD边与HG边是对应边,长度相等,∠ADC和∠FGH是对应角,大小相等.
解:x=∠ADC=360°-40°-95°-110°=115°,y=HG=3.
15.解:(1)∵△ABC与△ADE关于直线MN对称,ED=4 cm,
∴BC=ED=4 cm.
又∵FC=1 cm,
∴BF=BC-FC=3 cm.
(2)∵△ABC与△ADE关于直线MN对称,∠BAC=76°,
∴∠EAD=∠BAC=76°.
又∵∠EAC=58°,∴∠CAD=∠EAD-∠EAC=76°-58°=18°.
(3)直线MN垂直平分线段EC.
理由如图图下:∵点E,C关于直线MN对称,
∴直线MN垂直平分线段EC.
16.解:3 4 5 6 7 8
猜想:一个正n边形有n条对称轴.
17.解:(1)∵△BCD和△BED关于BD对称,
∴△BCD≌△BED.
∴BE=BC=10 cm.
∴AE=AB-BE=12-10=2(cm).
(2)∵△BCD≌△BED,∴DC=DE.
∴△ADE的周长=AE+AD+DE=AE+AC=8 cm.
[素养提升]
解:(1)证明:在长方形ABCD中,DA=BC,∠A=∠D=∠B=∠BCD=90°.
由折叠的性质,得GC=DA,∠G=∠D=90°,∠GCE=∠A=90°.
∴GC=BC,∠GCF+∠FCE=90°.
又∵∠FCE+∠BCE=90°,
∴∠GCF=∠BCE.
又∵∠G=∠B=90°,GC=BC,
∴△FGC≌△EBC(ASA).
(2)由(1)知,DF=GF=BE,
∴S四边形ECGF=S四边形AEFD=====16.
