全国人教版数学八年级上册课课练:13.2.1 作轴对称图形(含答案)
文档属性
| 名称 | 全国人教版数学八年级上册课课练:13.2.1 作轴对称图形(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 240.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-30 00:00:00 | ||
图片预览

文档简介
[作轴对称图形]
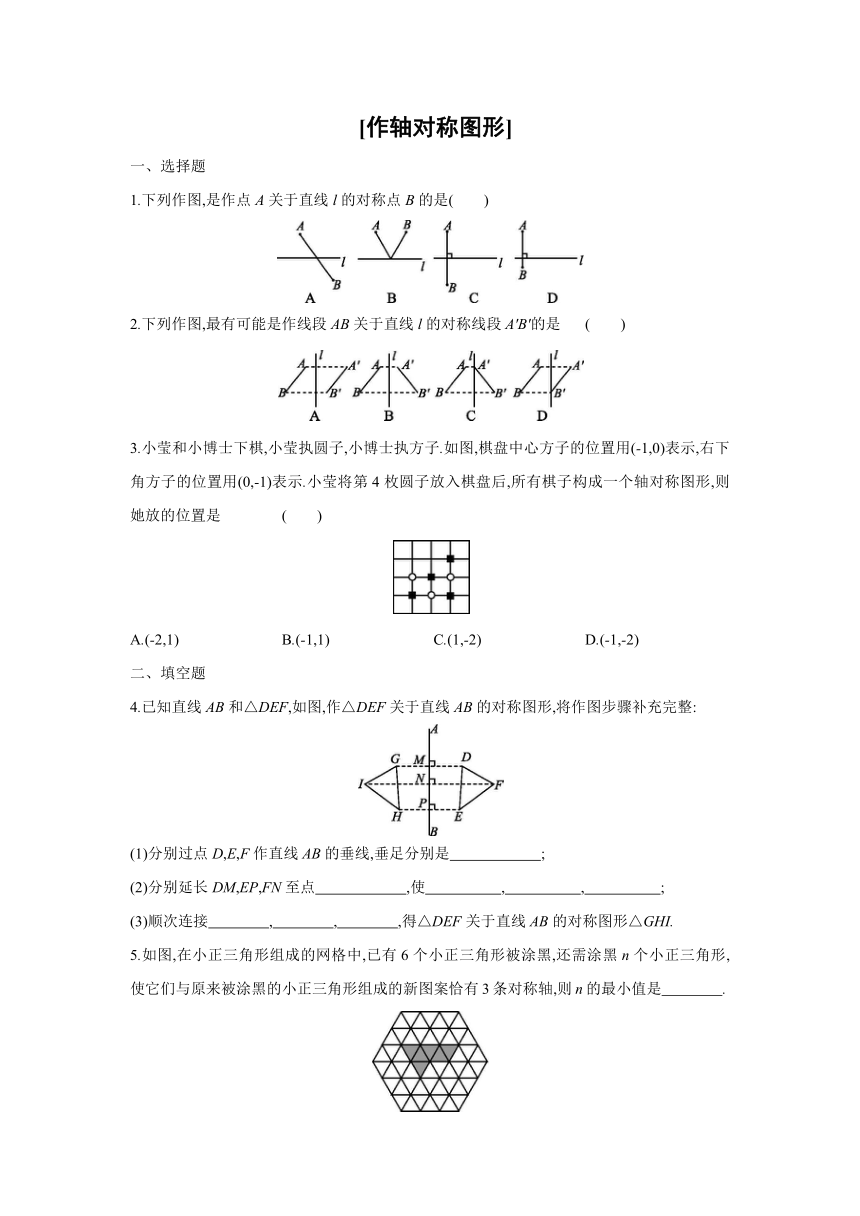
一、选择题
1.下列作图,是作点A关于直线l的对称点B的是( )
2.下列作图,最有可能是作线段AB关于直线l的对称线段A'B'的是 ( )
3.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,则她放的位置是 ( )
A.(-2,1) B.(-1,1) C.(1,-2) D.(-1,-2)
二、填空题
4.已知直线AB和△DEF,如图,作△DEF关于直线AB的对称图形,将作图步骤补充完整:
(1)分别过点D,E,F作直线AB的垂线,垂足分别是 ;
(2)分别延长DM,EP,FN至点 ,使 , , ;
(3)顺次连接 , , ,得△DEF关于直线AB的对称图形△GHI.
5.如图,在小正三角形组成的网格中,已有6个小正三角形被涂黑,还需涂黑n个小正三角形,使它们与原来被涂黑的小正三角形组成的新图案恰有3条对称轴,则n的最小值是 .
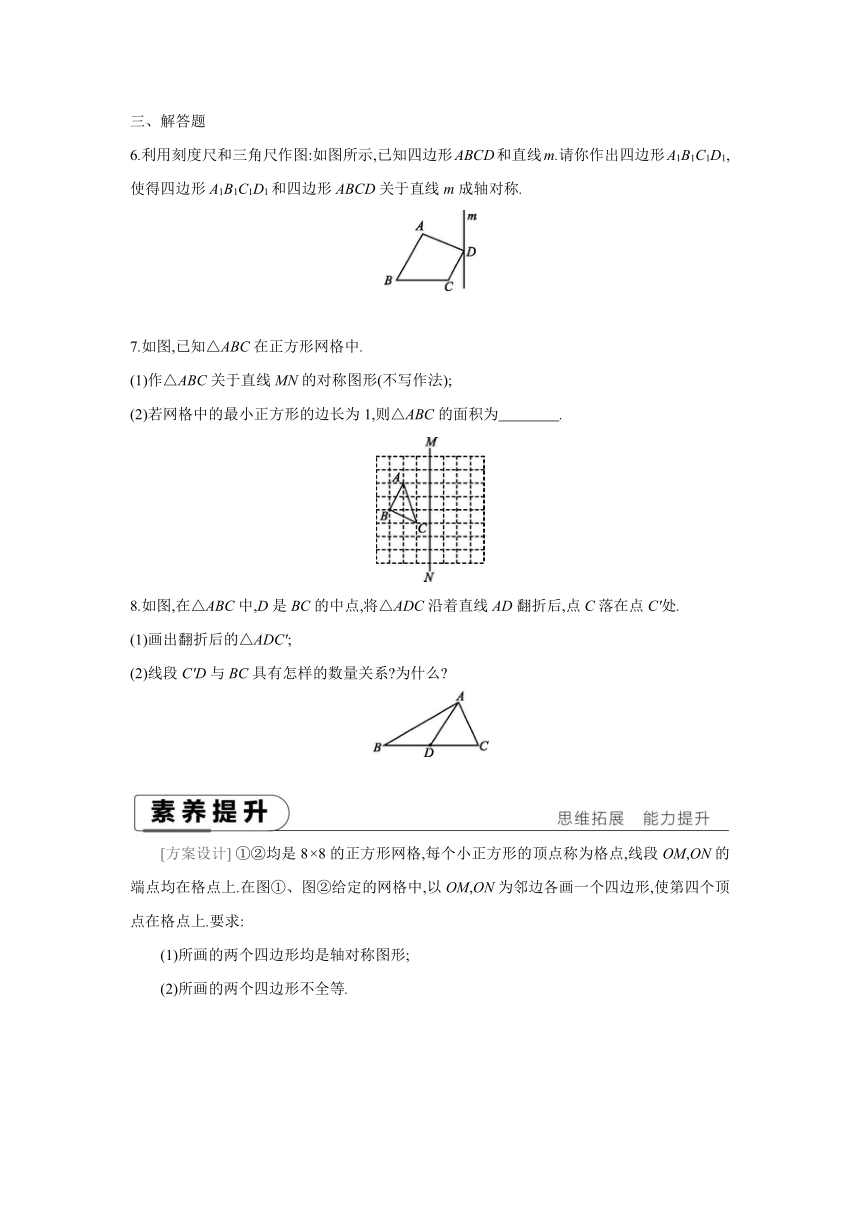
三、解答题
6.利用刻度尺和三角尺作图:如图所示,已知四边形ABCD和直线m.请你作出四边形A1B1C1D1,使得四边形A1B1C1D1和四边形ABCD关于直线m成轴对称.
7.如图,已知△ABC在正方形网格中.
(1)作△ABC关于直线MN的对称图形(不写作法);
(2)若网格中的最小正方形的边长为1,则△ABC的面积为 .
8.如图,在△ABC中,D是BC的中点,将△ADC沿着直线AD翻折后,点C落在点C'处.
(1)画出翻折后的△ADC';
(2)线段C'D与BC具有怎样的数量关系 为什么
[方案设计] ①②均是8×8的正方形网格,每个小正方形的顶点称为格点,线段OM,ON的端点均在格点上.在图①、图②给定的网格中,以OM,ON为邻边各画一个四边形,使第四个顶点在格点上.要求:
(1)所画的两个四边形均是轴对称图形;
(2)所画的两个四边形不全等.
答案
1.C 2.B
3.B 根据方子的位置可知对称轴是从左上斜向下的对角线所在的直线,由此可知第4枚圆子应放入棋盘(-1,1)的位置.故选B.
4.(1)M,P,N
(2)G,H,I MG=DM PH=EP NI=FN
(3)GH HI IG
5.3 如图所示,n的最小值为3.
6.解:如图,四边形A1B1C1D1即为所求.
7.解:(1)如图,分别作点A,B,C关于直线MN的对称点A',B',C',顺次连接A'B',B'C',C'A',则△A'B'C'即为所求.
(2)
8.解:(1)如图所示.
(2)BC=2C'D.理由:由折叠的性质,得CD=C'D.∵D是BC的中点,∴BC=2CD.∴BC=2C'D.
[素养提升]
解:如图所示:
一、选择题
1.下列作图,是作点A关于直线l的对称点B的是( )
2.下列作图,最有可能是作线段AB关于直线l的对称线段A'B'的是 ( )
3.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,则她放的位置是 ( )
A.(-2,1) B.(-1,1) C.(1,-2) D.(-1,-2)
二、填空题
4.已知直线AB和△DEF,如图,作△DEF关于直线AB的对称图形,将作图步骤补充完整:
(1)分别过点D,E,F作直线AB的垂线,垂足分别是 ;
(2)分别延长DM,EP,FN至点 ,使 , , ;
(3)顺次连接 , , ,得△DEF关于直线AB的对称图形△GHI.
5.如图,在小正三角形组成的网格中,已有6个小正三角形被涂黑,还需涂黑n个小正三角形,使它们与原来被涂黑的小正三角形组成的新图案恰有3条对称轴,则n的最小值是 .
三、解答题
6.利用刻度尺和三角尺作图:如图所示,已知四边形ABCD和直线m.请你作出四边形A1B1C1D1,使得四边形A1B1C1D1和四边形ABCD关于直线m成轴对称.
7.如图,已知△ABC在正方形网格中.
(1)作△ABC关于直线MN的对称图形(不写作法);
(2)若网格中的最小正方形的边长为1,则△ABC的面积为 .
8.如图,在△ABC中,D是BC的中点,将△ADC沿着直线AD翻折后,点C落在点C'处.
(1)画出翻折后的△ADC';
(2)线段C'D与BC具有怎样的数量关系 为什么
[方案设计] ①②均是8×8的正方形网格,每个小正方形的顶点称为格点,线段OM,ON的端点均在格点上.在图①、图②给定的网格中,以OM,ON为邻边各画一个四边形,使第四个顶点在格点上.要求:
(1)所画的两个四边形均是轴对称图形;
(2)所画的两个四边形不全等.
答案
1.C 2.B
3.B 根据方子的位置可知对称轴是从左上斜向下的对角线所在的直线,由此可知第4枚圆子应放入棋盘(-1,1)的位置.故选B.
4.(1)M,P,N
(2)G,H,I MG=DM PH=EP NI=FN
(3)GH HI IG
5.3 如图所示,n的最小值为3.
6.解:如图,四边形A1B1C1D1即为所求.
7.解:(1)如图,分别作点A,B,C关于直线MN的对称点A',B',C',顺次连接A'B',B'C',C'A',则△A'B'C'即为所求.
(2)
8.解:(1)如图所示.
(2)BC=2C'D.理由:由折叠的性质,得CD=C'D.∵D是BC的中点,∴BC=2CD.∴BC=2C'D.
[素养提升]
解:如图所示:
