圆的标准方程[上学期]
图片预览





文档简介
课件17张PPT。7.6 圆的标准方程求曲线方程的一般步骤1:建立适当的坐标系,用有序实数对(x,y)表示曲线上任意一点M的坐标;(建立坐标系,设点)
2:写出适合条件P的点M的集合P={M|P(M)}
3:用坐标表示P(M),列出方程f(x,y)=0;(列式)
4:化方程f(x,y)=0为最简形式; (化简)
5:证明化简后的方程的解为坐标的点都是曲线上的点。(证明)圆的轨迹圆的定义:
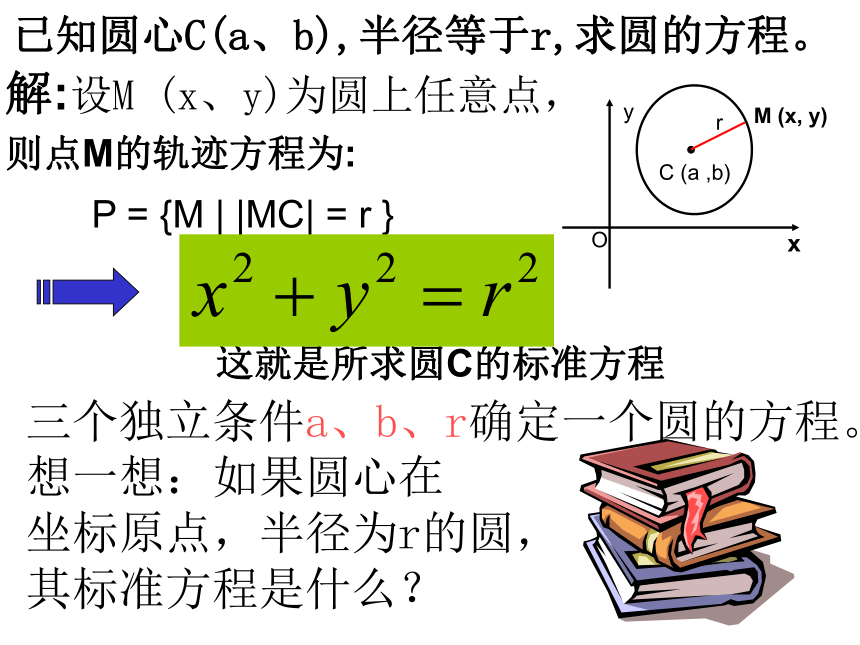
平面内与定点距离等于定长的点的集合(轨迹)是圆。定点就是圆心,定长就是半径。已知圆心C(a、b),半径等于r,求圆的方程。设M (x、y)为圆上任意点,(x-a)2+(y-b)2=r2三个独立条件a、b、r确定一个圆的方程。想一想:如果圆心在
坐标原点,半径为r的圆,
其标准方程是什么?解:则点M的轨迹方程为:P = {M | |MC| = r }这就是所求圆C的标准方程圆的标准方程(1)方程中参数a、b、r的意义是什么?
(2)当圆心在原点时圆的方程的形式是什么?
(3)要确定一个圆的方程,至少需要几个独立条件?
(4)明确给出了圆的大小(半径)和圆的位置(圆心)
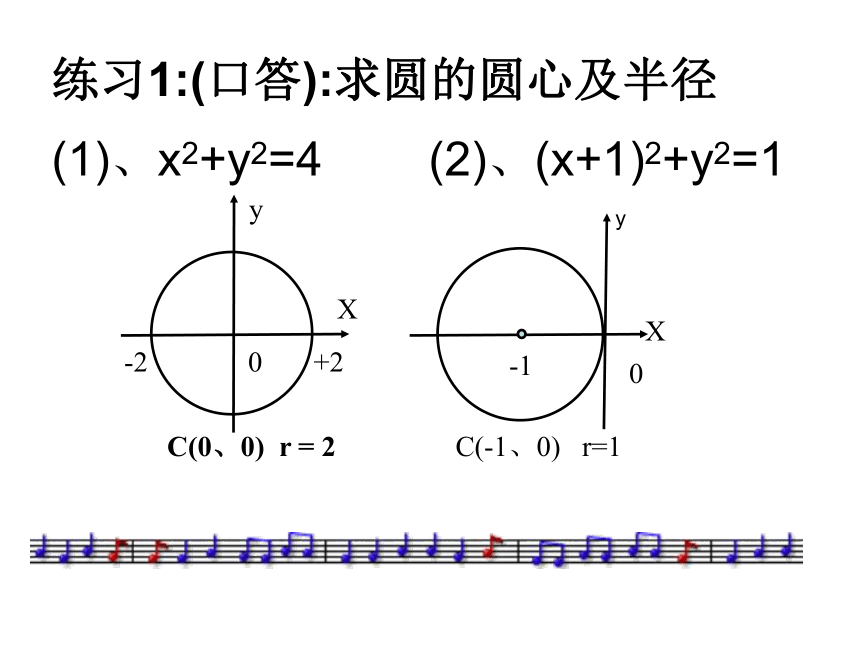
------几何特征(x-a)2+(y-b)2=r2练习1:(口答):求圆的圆心及半径(1)、x2+y2=4 (2)、(x+1)2+y2=1练习2:写出下列圆的方程1、圆心在原点,半径为3。
2、圆心在(3,4),半径为
(1) x2+y2=9(2) (x-3)2+(y-4)2=5解:例1、求以c(1,3)为圆心,并和直线3x - 4y - 6 =0相切的圆的方程。解:练习:求圆心在(-1, 2),与y轴相切的圆的方程
所求圆的方程为:(x+1)2+(y-2)2=1解:练习:求圆心在直线y=x上,同时和两坐标轴相切,半径为2的圆的方程.解:(x-2)2+(y-2)2=4
(x+2)2+(y+2)2=4依题意得所求圆的方程为 练习:已知圆经过P(5,1),圆心在C(8,3),求圆的方程。 解:练习:已知两点A(4,9),B(6,3),求以
AB为直径的圆的方程.解:可用两点间距离公式求r练习:解:解方程组:例2解一:练习:解:解:解:例3解:代入圆的方程得练习:赵州桥的跨度为37.4米,拱高7.2米,求这座圆拱桥的拱圆所在的圆方程。解:代入圆的方程得1、圆的标准方程.
2、圆的标准方程的简单应用.作业 :习题7.7 1、 2、 3. 4四、小结:再见!同学们
2:写出适合条件P的点M的集合P={M|P(M)}
3:用坐标表示P(M),列出方程f(x,y)=0;(列式)
4:化方程f(x,y)=0为最简形式; (化简)
5:证明化简后的方程的解为坐标的点都是曲线上的点。(证明)圆的轨迹圆的定义:
平面内与定点距离等于定长的点的集合(轨迹)是圆。定点就是圆心,定长就是半径。已知圆心C(a、b),半径等于r,求圆的方程。设M (x、y)为圆上任意点,(x-a)2+(y-b)2=r2三个独立条件a、b、r确定一个圆的方程。想一想:如果圆心在
坐标原点,半径为r的圆,
其标准方程是什么?解:则点M的轨迹方程为:P = {M | |MC| = r }这就是所求圆C的标准方程圆的标准方程(1)方程中参数a、b、r的意义是什么?
(2)当圆心在原点时圆的方程的形式是什么?
(3)要确定一个圆的方程,至少需要几个独立条件?
(4)明确给出了圆的大小(半径)和圆的位置(圆心)
------几何特征(x-a)2+(y-b)2=r2练习1:(口答):求圆的圆心及半径(1)、x2+y2=4 (2)、(x+1)2+y2=1练习2:写出下列圆的方程1、圆心在原点,半径为3。
2、圆心在(3,4),半径为
(1) x2+y2=9(2) (x-3)2+(y-4)2=5解:例1、求以c(1,3)为圆心,并和直线3x - 4y - 6 =0相切的圆的方程。解:练习:求圆心在(-1, 2),与y轴相切的圆的方程
所求圆的方程为:(x+1)2+(y-2)2=1解:练习:求圆心在直线y=x上,同时和两坐标轴相切,半径为2的圆的方程.解:(x-2)2+(y-2)2=4
(x+2)2+(y+2)2=4依题意得所求圆的方程为 练习:已知圆经过P(5,1),圆心在C(8,3),求圆的方程。 解:练习:已知两点A(4,9),B(6,3),求以
AB为直径的圆的方程.解:可用两点间距离公式求r练习:解:解方程组:例2解一:练习:解:解:解:例3解:代入圆的方程得练习:赵州桥的跨度为37.4米,拱高7.2米,求这座圆拱桥的拱圆所在的圆方程。解:代入圆的方程得1、圆的标准方程.
2、圆的标准方程的简单应用.作业 :习题7.7 1、 2、 3. 4四、小结:再见!同学们
