9.1三角形的边 课件(共18张PPT)
文档属性
| 名称 | 9.1三角形的边 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 14:31:20 | ||
图片预览





文档简介
(共18张PPT)
猜谜
形状似座山,稳定性能坚.
三竿首尾连,学问不简单.
三角形的边
导入新课
生活中三角形
情景引入
讲授新课
三角形的有关概念
三角形的定义:由不在同一条直线上的三条线段首尾顺次相接所构成的图形叫作三角形.
问题1:结合上图你能试着说一说三角形的定义吗?
问题2:图中有几个三角形?如何表示?
三角形的有关概念
A
B
C
a
c
b
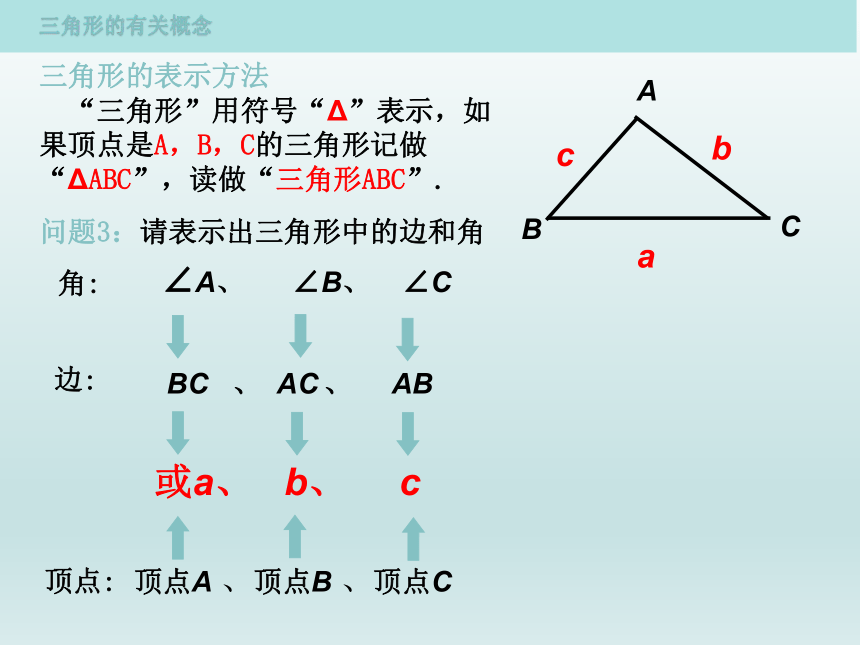
问题3:请表示出三角形中的边和角
BC 、 AC 、 AB
顶点:
∠A、 ∠B、 ∠C
或a、 b、 c
边:
角:
顶点A 、顶点B 、顶点C
三角形的表示方法
“三角形”用符号“Δ”表示,如果顶点是A,B,C的三角形记做“ΔABC”,读做“三角形ABC”.
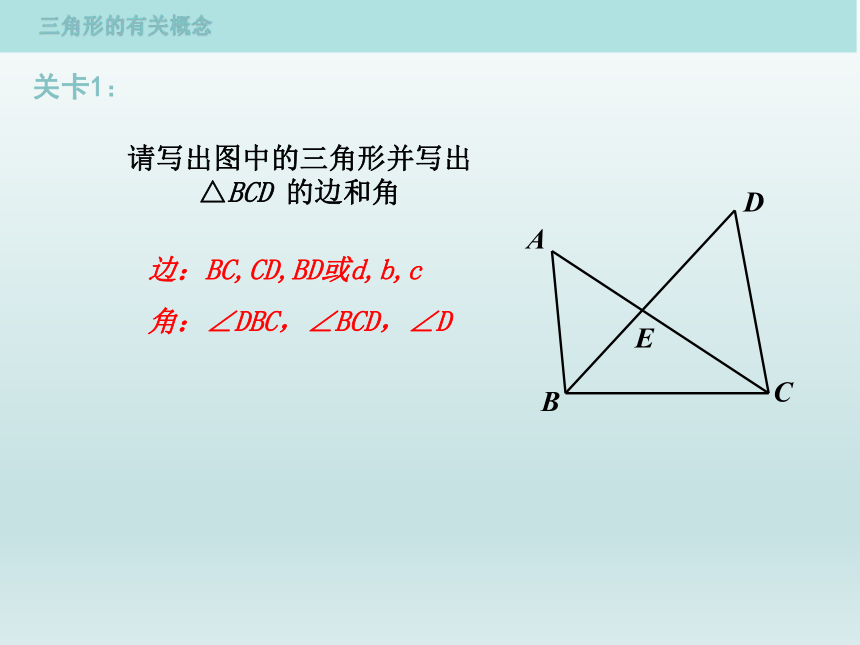
关卡1:
A
B
C
D
E
请写出图中的三角形并写出△BCD 的边和角
边:BC,CD,BD或d,b,c
角:∠DBC,∠BCD,∠D
三角形的有关概念
三角形三边关系------实验探究
实验探究:
1.动手做一做:请随意拿取三根纸棒,将其粘在A4纸上,你能拼成三角形吗?展示你的作品。
2.仔细量一量:同组成员所拼成的三角形的两条边的长度和与第三条边有什么关系?
3.认真想一想:关于三角形三边关系你有何猜想?请把猜想写成命题形式。
4.试着证一证:对你的猜想给与证明
从A到C你会选择哪条路?
证:
∵AB为线段
∴AC+BC>AB(两点之间线段最短)
同理,AB+BC>AC
AC+AB>BC
三角形三边关系------理论证明
C
A
B
三角形的三边关系:
三角形任意两边的和大于第三边。
三角形三边关系------得出结论
三角形三边关系-----例题简析
关卡2:三条线段的长度如下:
(1)1.5cm 2cm 2.5cm
(2) 2cm 3cm 1cm
(3) 1cm 4cm 4cm
哪一组线段能构成三角形?
一定要验证三组两两相加吗?
思考:
已知一个三角形的一边为17cm,另两边分别为22cm和 acm , a的取值范围是什么?
三角形三边关系-----解决问题
三角形的三边关系:
任意两边的差<第三边<任意两边的和
三角形三边关系------得出结论
三角形
(按边分)
不等边三角形
等腰三角形
等腰三角形
(底边和腰不相等的等腰三角形)
等边三角形
(底边和腰相等的等腰三角形)
锐角三角形
直角三角形
钝角三角形
三角形
(按角分)
三角形的分类
三角形
相关概念
三角形的分类
三边的关系:
三角形定义
三角形的边、顶点、角
任意两边的差<第三边<任意两边的和
不等边三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
课堂小结
过关练习
1.若长度分别是a,3,5的三条线段能组成一个三角形,则a的值可以是?
A.1 B.2 C.4 D.8
2.以8,9,x为一个三角形的三边,则第三边x的取值范围是___
3.已知等腰三角形的一边等于5,一边等于11,求它的周长___
争做数学小勇士
作业:课本102页3.4题
答案: 1.C
2.13.27(分类思想的同时注意是否能构成三角形)
谢谢观看
猜谜
形状似座山,稳定性能坚.
三竿首尾连,学问不简单.
三角形的边
导入新课
生活中三角形
情景引入
讲授新课
三角形的有关概念
三角形的定义:由不在同一条直线上的三条线段首尾顺次相接所构成的图形叫作三角形.
问题1:结合上图你能试着说一说三角形的定义吗?
问题2:图中有几个三角形?如何表示?
三角形的有关概念
A
B
C
a
c
b
问题3:请表示出三角形中的边和角
BC 、 AC 、 AB
顶点:
∠A、 ∠B、 ∠C
或a、 b、 c
边:
角:
顶点A 、顶点B 、顶点C
三角形的表示方法
“三角形”用符号“Δ”表示,如果顶点是A,B,C的三角形记做“ΔABC”,读做“三角形ABC”.
关卡1:
A
B
C
D
E
请写出图中的三角形并写出△BCD 的边和角
边:BC,CD,BD或d,b,c
角:∠DBC,∠BCD,∠D
三角形的有关概念
三角形三边关系------实验探究
实验探究:
1.动手做一做:请随意拿取三根纸棒,将其粘在A4纸上,你能拼成三角形吗?展示你的作品。
2.仔细量一量:同组成员所拼成的三角形的两条边的长度和与第三条边有什么关系?
3.认真想一想:关于三角形三边关系你有何猜想?请把猜想写成命题形式。
4.试着证一证:对你的猜想给与证明
从A到C你会选择哪条路?
证:
∵AB为线段
∴AC+BC>AB(两点之间线段最短)
同理,AB+BC>AC
AC+AB>BC
三角形三边关系------理论证明
C
A
B
三角形的三边关系:
三角形任意两边的和大于第三边。
三角形三边关系------得出结论
三角形三边关系-----例题简析
关卡2:三条线段的长度如下:
(1)1.5cm 2cm 2.5cm
(2) 2cm 3cm 1cm
(3) 1cm 4cm 4cm
哪一组线段能构成三角形?
一定要验证三组两两相加吗?
思考:
已知一个三角形的一边为17cm,另两边分别为22cm和 acm , a的取值范围是什么?
三角形三边关系-----解决问题
三角形的三边关系:
任意两边的差<第三边<任意两边的和
三角形三边关系------得出结论
三角形
(按边分)
不等边三角形
等腰三角形
等腰三角形
(底边和腰不相等的等腰三角形)
等边三角形
(底边和腰相等的等腰三角形)
锐角三角形
直角三角形
钝角三角形
三角形
(按角分)
三角形的分类
三角形
相关概念
三角形的分类
三边的关系:
三角形定义
三角形的边、顶点、角
任意两边的差<第三边<任意两边的和
不等边三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
课堂小结
过关练习
1.若长度分别是a,3,5的三条线段能组成一个三角形,则a的值可以是?
A.1 B.2 C.4 D.8
2.以8,9,x为一个三角形的三边,则第三边x的取值范围是___
3.已知等腰三角形的一边等于5,一边等于11,求它的周长___
争做数学小勇士
作业:课本102页3.4题
答案: 1.C
2.1
谢谢观看
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
