11.3.2 多边形的外角和 课件(共20张PPT)
文档属性
| 名称 | 11.3.2 多边形的外角和 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 21:20:28 | ||
图片预览




文档简介
(共20张PPT)
多边形外角和定理
咱班跑完一圈,方向改变了多少度?
多 边 形
外 角 和 定 理
1.三角形的外角
每个顶点处有两个外角,它们是对顶角.
六个.
探究新知
A
B
C
D
复 习 回 顾
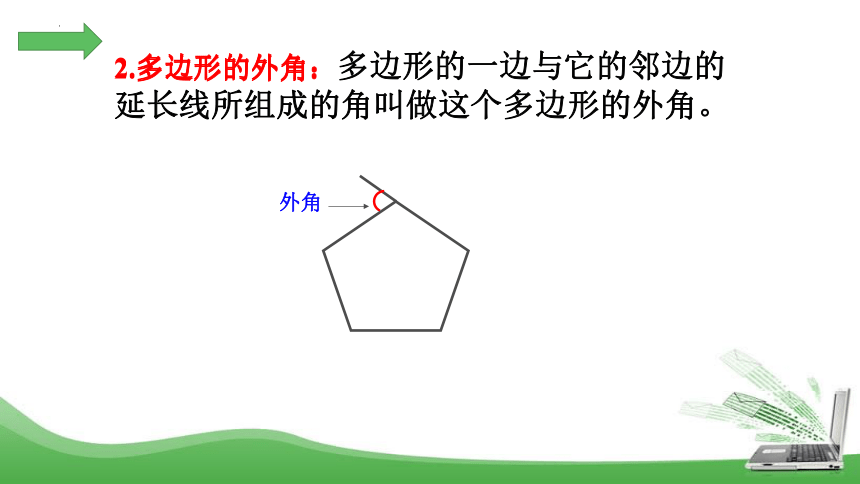
2.多边形的外角:多边形的一边与它的邻边的延长线所组成的角叫做这个多边形的外角。
外角
2.多边形的外角:
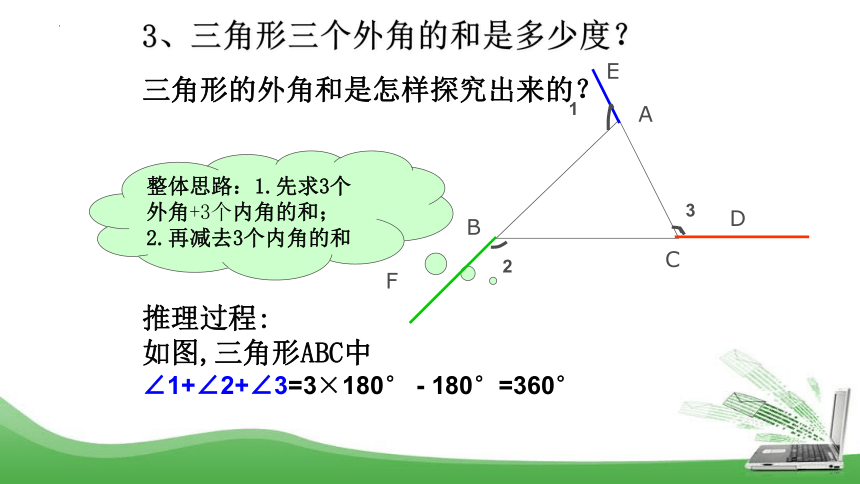
整体思路:1.先求3个外角+3个内角的和;
2.再减去3个内角的和
推理过程:
如图,三角形ABC中
∠1+∠2+∠3=3×180° - 180°=360°
A
B
C
D
E
F
2
1
3
3、三角形三个外角的和是多少度?
三角形的外角和是怎样探究出来的?
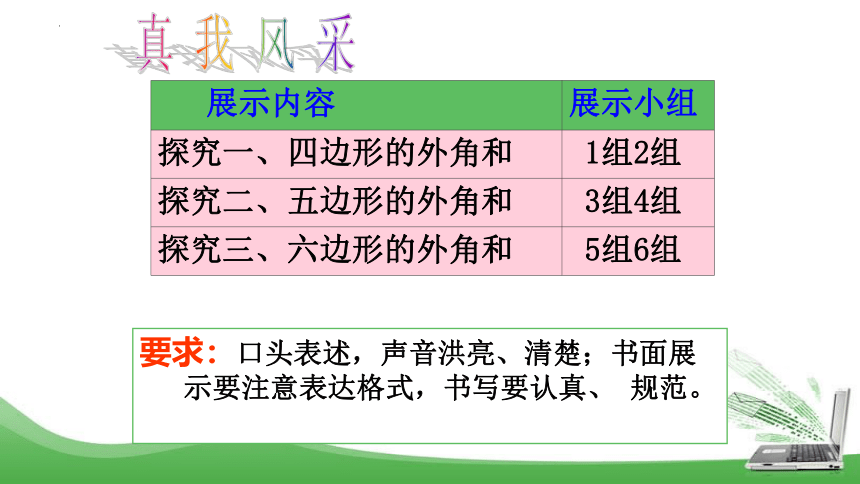
展示内容 展示小组
探究一、四边形的外角和 1组2组
探究二、五边形的外角和 3组4组
探究三、六边形的外角和 5组6组
要求:口头表述,声音洪亮、清楚;书面展示要注意表达格式,书写要认真、 规范。
真 我 风 采
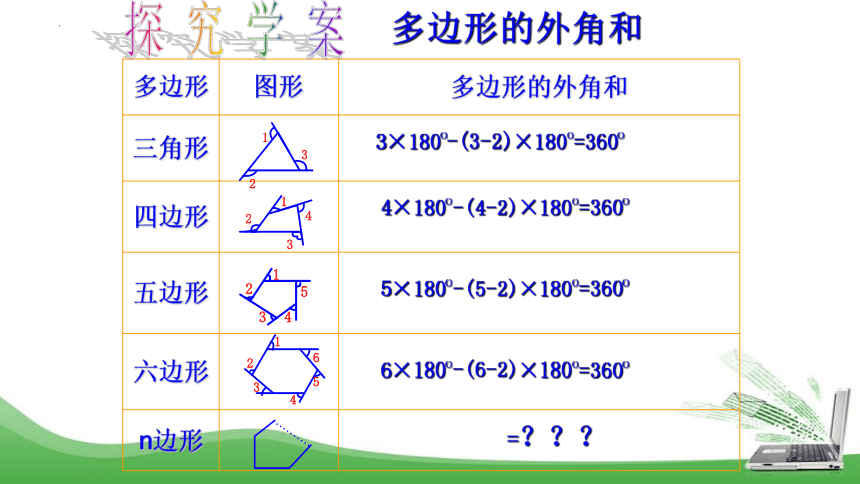
多边形 图形 多边形的外角和
三角形
四边形
五边形
六边形
n边形
3×180o-(3-2)×180o=360o
4×180o-(4-2)×180o=360o
5×180o-(5-2)×180o=360o
6×180o-(6-2)×180o=360o
多边形的外角和
探 究 学 案
=???
推论:任意多边形的外角 和
等于360 。
类比前边的做法,你能归纳出n边形的外角和是多少吗?
∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________
A1
A2
A3
An
A4
证明:
180 ,
(n-2) 180 ,
∴ n 边形的外角和等于n 180 – (n-2) 180 =360 。
n 180 ,
还有没有其它方法可以推导出多边形外角和
想一想:
多边形的外角和等于360°
多边形的外角和定理:
归 纳:
【学以致用1.外角和定理直接应用】
1.判断.
(1)当多边形边数增加时,它的内角和也随着加.( )
(2)当多边形边数增加时,它的外角和也随着加.( )
(3)三角形的外角和与八边形的外角和相等. ( )
2.一个多边形的每一个外角都等于72 ,这个多边形是几边形?
学以致用2:生活实例,外角速算
3.如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是________米.
150
【变式】如图所示小华从点A出发,沿直线前进10米后左转一定角度,再沿直线前进10米,又向左转同样角度,照这样走下去,他第一次回到出发地点A时,走的路程一共是100米,
则他每次转过的角度是___ °.
A
36
学以致用3:内外角结合,方程救助!
4.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解:设多边形的边数为n,
则它的内角和为 (n-2)×180°,它的外角和等于360°,
∴ (n-2)×180°=2× 360
解得 n=6
答:这个多边形的边数为6。
3.如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____.
12
1.十五边形的外角和为_____.
360o
2.已知一个多边形的每一个外角都是60o,这个多边形的边数为______.
6
练习
4.若一个多边形的内角和与它的外角和相等,求该多边形的边数.
5.一个多边形的外角和是内角和的 ,它是几边形?
交流收获
1.多边形的外角和是多少度?
数学知识是无穷的。只要我们能善于运用数学思想方法去探究数学问题,所获得
的数学知识就会越来越多!
—教师寄语
请同学们谈一谈本节课你有哪些收获
2.多边形外角和的推导过程.
3.这节课你体会到了哪些数学思想方法?
分层作业
A.课本24页3题、6题;(5分钟)
B.同步训练15页;(10分钟)
C.学案上的选做题。(10分钟)
多边形外角和定理
咱班跑完一圈,方向改变了多少度?
多 边 形
外 角 和 定 理
1.三角形的外角
每个顶点处有两个外角,它们是对顶角.
六个.
探究新知
A
B
C
D
复 习 回 顾
2.多边形的外角:多边形的一边与它的邻边的延长线所组成的角叫做这个多边形的外角。
外角
2.多边形的外角:
整体思路:1.先求3个外角+3个内角的和;
2.再减去3个内角的和
推理过程:
如图,三角形ABC中
∠1+∠2+∠3=3×180° - 180°=360°
A
B
C
D
E
F
2
1
3
3、三角形三个外角的和是多少度?
三角形的外角和是怎样探究出来的?
展示内容 展示小组
探究一、四边形的外角和 1组2组
探究二、五边形的外角和 3组4组
探究三、六边形的外角和 5组6组
要求:口头表述,声音洪亮、清楚;书面展示要注意表达格式,书写要认真、 规范。
真 我 风 采
多边形 图形 多边形的外角和
三角形
四边形
五边形
六边形
n边形
3×180o-(3-2)×180o=360o
4×180o-(4-2)×180o=360o
5×180o-(5-2)×180o=360o
6×180o-(6-2)×180o=360o
多边形的外角和
探 究 学 案
=???
推论:任意多边形的外角 和
等于360 。
类比前边的做法,你能归纳出n边形的外角和是多少吗?
∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________
A1
A2
A3
An
A4
证明:
180 ,
(n-2) 180 ,
∴ n 边形的外角和等于n 180 – (n-2) 180 =360 。
n 180 ,
还有没有其它方法可以推导出多边形外角和
想一想:
多边形的外角和等于360°
多边形的外角和定理:
归 纳:
【学以致用1.外角和定理直接应用】
1.判断.
(1)当多边形边数增加时,它的内角和也随着加.( )
(2)当多边形边数增加时,它的外角和也随着加.( )
(3)三角形的外角和与八边形的外角和相等. ( )
2.一个多边形的每一个外角都等于72 ,这个多边形是几边形?
学以致用2:生活实例,外角速算
3.如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是________米.
150
【变式】如图所示小华从点A出发,沿直线前进10米后左转一定角度,再沿直线前进10米,又向左转同样角度,照这样走下去,他第一次回到出发地点A时,走的路程一共是100米,
则他每次转过的角度是___ °.
A
36
学以致用3:内外角结合,方程救助!
4.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。
解:设多边形的边数为n,
则它的内角和为 (n-2)×180°,它的外角和等于360°,
∴ (n-2)×180°=2× 360
解得 n=6
答:这个多边形的边数为6。
3.如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____.
12
1.十五边形的外角和为_____.
360o
2.已知一个多边形的每一个外角都是60o,这个多边形的边数为______.
6
练习
4.若一个多边形的内角和与它的外角和相等,求该多边形的边数.
5.一个多边形的外角和是内角和的 ,它是几边形?
交流收获
1.多边形的外角和是多少度?
数学知识是无穷的。只要我们能善于运用数学思想方法去探究数学问题,所获得
的数学知识就会越来越多!
—教师寄语
请同学们谈一谈本节课你有哪些收获
2.多边形外角和的推导过程.
3.这节课你体会到了哪些数学思想方法?
分层作业
A.课本24页3题、6题;(5分钟)
B.同步训练15页;(10分钟)
C.学案上的选做题。(10分钟)
