14.1.1 同底数幂的乘法 课件(共21张PPT)
文档属性
| 名称 | 14.1.1 同底数幂的乘法 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 21:18:09 | ||
图片预览







文档简介
(共21张PPT)
中物理
人教版 数学八年级上册
第十四章 整式的乘法与因式分解
14.1 整式的乘法
14.1.1 同底数幂的乘法
前言
学习目标
重点
运用同底数幂的乘法性质计算和应用。
难点
同底数幂的乘法性质的推导和灵活应用。
1、感受生活中幂的运算的存在价值。
2、经历自主探究同底数幂的乘法的运算性质的过程。
能用代数式和文字表述性质,感受公式的抽象美、
简洁美、对称美,并会用性质计算。
3、逐步形成独立思考、主动探索的习惯,感悟科技
的飞速发展和祖国的强大。
4、通过由特殊到一般的猜想与说理、验证,
培养学生归纳表达能力
2021年10月16日,中国3名航天员翟志刚、王亚平、叶光富开启了6个月的空间生活。号称“快递小哥”的天舟三号,若要按时送达补给物资,需要精准的计算,如果使用的计算,每秒可达1016次运算,那么它工作103秒可进行多少次运算
情景导入
1016×103
= ?
=( 10×10×‥‥‥×10 )
19个
=(10×10×‥‥‥×10)×(10×10×10)
= 1019
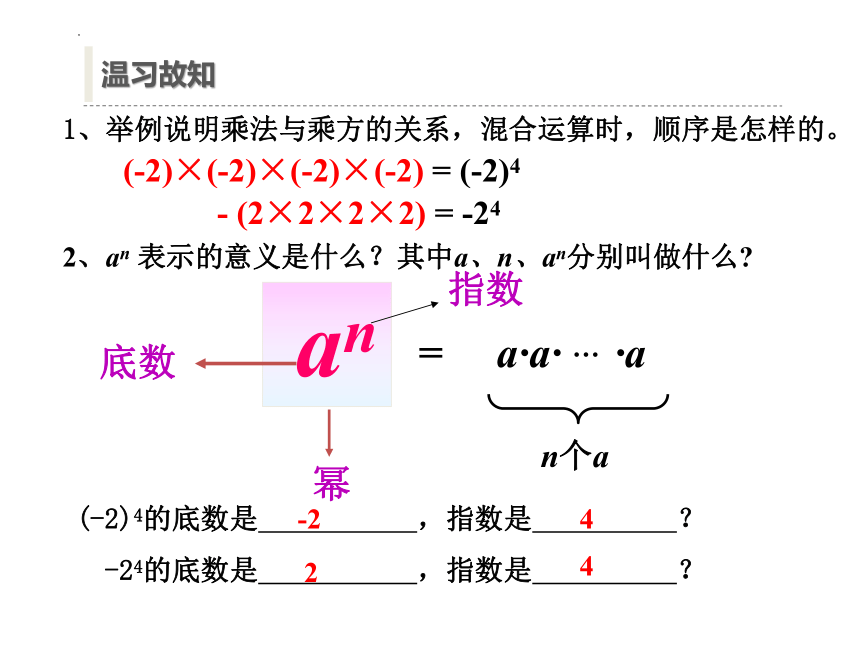
= a·a· … ·a
n个a
2、an 表示的意义是什么?其中a、n、an分别叫做什么
an
底数
幂
指数
(-2)4的底数是 ,指数是 ?
-24的底数是 ,指数是 ?
(-2)×(-2)×(-2)×(-2) = (-2)4
- (2×2×2×2) = -24
温习故知
1、举例说明乘法与乘方的关系,混合运算时,顺序是怎样的。
-2
2
4
4
问题一:根据乘方的意义填空(结果写成幂的形式) 。
问题二:观察左右两边,底数、指数各有什么关系?
问题三:得出你的猜想,并尝试证明你的猜想是否正确。
(1). 23 × 24 =(2 ×2×2)×(2×2×2×2)= 2 ( 3+4 ) =2( 7 )
(2).(—)3×(—)4=( × × )×( × × × )= (—)( ) = (—)( )
(3).0.53 × 0.54 =( × × )× ( × × × )= 0.5( ) =0.5( )
(4).(-3)3 ×(-3)4 =[ × × ]× [ × × × ]=(-3) ( ) =(-3) ( )
(5). a3 · a4 =( · · ) · ( · · · ) = a ( ) = a ( )
(7).(a+b)3×(a+b)4=[ × × ]× [ × × × ]=(a+b)( ) =(a+b)( )
探索新知
2
3
2
3
2
3
(6).(mn)3×(mn)4=[ × × ]× [ × × × ]=(mn) ( ) =(mn) ( )
边思考边解答呦!
2
3
问题一:根据乘方的意义填空(结果写成幂的形式) 。
(1). 23 × 24 = 2 ( )
(2). 0.53 × 0.54 =0.5 ( )
(3).(—)3 × (—)4 =(— ) ( )
(4).(-3)3 × (-3)4 = (-3) ( )
(5). a3 · a4 = a ( )
(6).(mn)3×(mn)4 =(mn)( )
(7).(a+b)3×(a+b)4=(a+b)( )
3+4
猜想: am · an= (m、n都是正整数)
3+4
3+4
3+4
3+4
探索新知
2
3
2
3
2
3
3+4
问题二:观察左右两边,发现底数、指数各有什么规律?
问题三:得出你的猜想,并尝试证明。
3+4
am · an =
=am+n
= aa…a
(m+n)个a
m个a
(aa…a )
n个a
(aa…a)
am · an= (m、n都是正整数)
am+n
(乘法结合律)
(乘方的意义)
归纳、证明
证明:
获得新知
am · an =
同底数幂相乘,
底数 ,指数 。
不变
相加
同底数幂的乘法性质:
am+n (m、n都是正整数)
注意事项:
1.条件:①底数相同,②乘法运算。
2.结果:①底数不变, ②将指数相加。
如:43×45=
43+5
=48
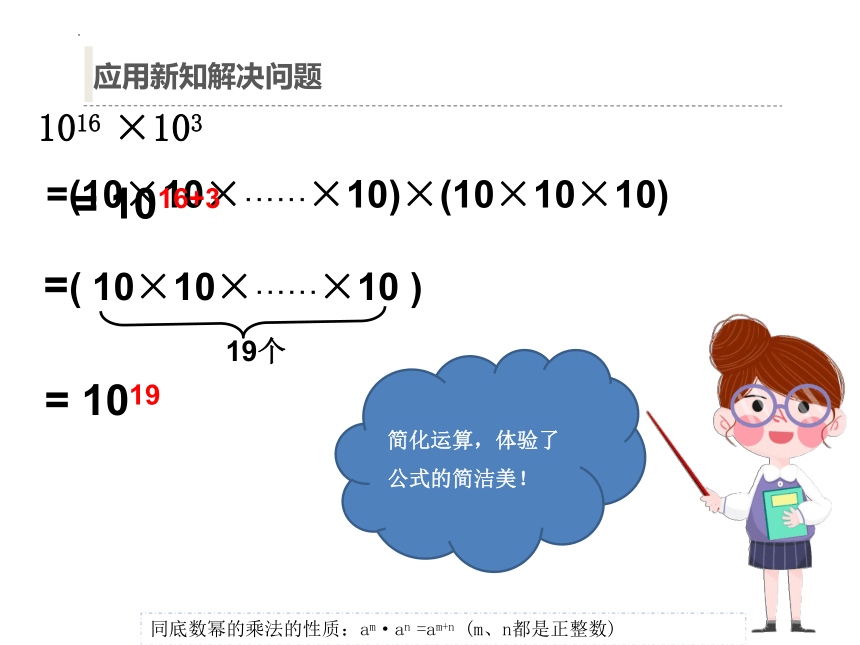
1016 ×103
= 1019
=(10×10×‥‥‥×10)×(10×10×10)
=( 10×10×‥‥‥×10 )
19个
= 1016+3
简化运算,体验了公式的简洁美!
应用新知解决问题
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数)
想一想: 当三个或三个以上同底数幂相乘时,是否也具有这一
性质呢?怎样用公式表示?
如 am · an · ap ?
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数)
公式的推广
例1 计算,结果用幂的形式表示:
(1)x2·x5; (2)a·a6;
(3)(-2)×(-2)4×(-2)3;(4)xm·x3m+1
a=a1
同底数幂的乘法性质:am·an =am+n (m、n都是正整数)
典型例题
1、计算:
(1)105×106=_____; (2)a7·a3=_______;
(3)x5·x7=_______; (4)(-b)3·(-b)2=__________.
2、判断下面的计算对不对?如果不对,应当怎样改正.
(1)b3·b3=2b3
(2)b3+b3=b6
(3)a·a5·a3=a8
(4)(-x)4·(-x)4=(-x)16
1011
a10
x12
(-b)5
=-b5
×
×
×
×
b6
2b3
=x8
a9
(-x)8
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数)
基础训练(抢答)
常见变形:(-a)2=a2, (-a)3=-a3
3、计算结果用幂的形式表示:
(1)(- —) ×(- —)2 × (- —)3 (2)y3×(-y)2
(3)(a+b)4·(a+b)7 (4)2m×2n×8
同底数幂的乘法性质:am·an =am+n (m、n都是正整数)
典型计算
1
3
1
3
1
3
4、判断下面的说法是否正确,如果正确请说明理由,如果不正确请举出反例:
两个幂相乘,如果底数不同就一定不能用性质计算。
请计算:(x-y)2·(y-x)5.
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数)
进阶练习
方法总结:
(1)当底数不同的幂相乘时,化为同底数的幂进行计算;
(2)当底数互为相反数的幂相乘时,根据幂的符号规律,可把不
同底数的幂化成同底数的幂相乘.
,n为偶数
,n为奇数
(a-b)n=
(b-a)n
-(b-a)n
常见变形:(-a)2=a2, (-a)3=-a3 ;
5、2022年4月16日,搭载“太空三人组”的神州十三号载人飞船结束了6个月的“太空出差”。已知神舟飞船在轨道上运行的速度大约为7.8 × 103米/秒,接近第一宇宙速度,那么这半年(大约1.6 × 107秒 )飞行了多少路程
实际应用
解:(7.8×103)×(1.6×107 )
=(7.8 × 1.6)×(103×107)
=12.48× 1010
答:太空三人组这半年共飞行了 1.248× 1011 米。
=1.248× 1011 (米)
【想一想】am+n可以写成哪两个因式的积?
公式的逆用
am+n=am·an
【填一填】若xm=3,xn=2,那么,
(1)xm+n= × = × = ;
(2)x2m= × = × =_ ;
(3)x2m+n= × = × = .
xm
xn
6
3
2
xm
xm
3
3
9
x2m
xn
9
2
18
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数)
=( ) × ( )
x10
【试一试】
6、 (1)若xa=3,xb=4,求xa+b的值.
(2)已知23x+2=32,求x的值;
方法总结:
(1) 逆用同底数幂的乘法性质,将所求代数式转化为几个已知因式的乘积的形式,然后再求值.
(2) 将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
拓展延伸
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数);逆用: am+n = am·an(m、n都是正整数)
通过对本节课的学习,
你有哪些收获呢?
同底数幂的乘法
性质
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用公式
常见变形:(-a)2n=a2n, (-a)2n+1=-a2n+1,
底数相同时
底数不相同时
先变成同底数再应用公式
课堂小结
am·an=am+n (m,n都是正整数)
,n为偶数
,n为奇数
(a-b)n=
(b-a)n
-(b-a)n
1.下列各式的结果等于26的是( )
A.2+25 B.2·25 C.23·25 D.0.22·0.24
2.下列计算结果正确的是( )
A.a3·a3=a9 B.m2·n2=mn4 C.xm·x3=x3m D.y·yn=yn+1
3.计算:(1)xn+1·x2n=_______;(2)(a-b)2·(a-b)3=_______;
(3)-a4·(-a)2=_____;(4)y4·y3·y2·y =_______.
4.填空:
(1)x·x2·x( )=x7;(2)xm·( )=x3m;(3)8×4=2x,则x=( )
B
D
4
5
x2m
-a6
y10
变式训练、自我检验
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数);逆用: am+n = am·an(m、n都是正整数)
x3n+1
(a-b)5
(2 )=
(a )=
(a )=
(a )=
3
3
4
4
m
4
n
m
1、必做题目:课本第96页练习(2)(4),习题14.1第1.(1)(2)题。
2、开放性题目:请给你的同桌用2、3、a、b(a、b为正整数)编计算题。要求如下:(1)所编题目为同底数幂乘法计算题;
(2)以上字母或者数字最多用两次。
3、探究题目:用同底数幂相乘的运算法则计算并观察底数和指数的变化规律。(选做)
课后作业与探究
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数);逆用: am+n = am·an(m、n都是正整数)
中物理
人教版 数学八年级上册
第十四章 整式的乘法与因式分解
14.1 整式的乘法
14.1.1 同底数幂的乘法
前言
学习目标
重点
运用同底数幂的乘法性质计算和应用。
难点
同底数幂的乘法性质的推导和灵活应用。
1、感受生活中幂的运算的存在价值。
2、经历自主探究同底数幂的乘法的运算性质的过程。
能用代数式和文字表述性质,感受公式的抽象美、
简洁美、对称美,并会用性质计算。
3、逐步形成独立思考、主动探索的习惯,感悟科技
的飞速发展和祖国的强大。
4、通过由特殊到一般的猜想与说理、验证,
培养学生归纳表达能力
2021年10月16日,中国3名航天员翟志刚、王亚平、叶光富开启了6个月的空间生活。号称“快递小哥”的天舟三号,若要按时送达补给物资,需要精准的计算,如果使用的计算,每秒可达1016次运算,那么它工作103秒可进行多少次运算
情景导入
1016×103
= ?
=( 10×10×‥‥‥×10 )
19个
=(10×10×‥‥‥×10)×(10×10×10)
= 1019
= a·a· … ·a
n个a
2、an 表示的意义是什么?其中a、n、an分别叫做什么
an
底数
幂
指数
(-2)4的底数是 ,指数是 ?
-24的底数是 ,指数是 ?
(-2)×(-2)×(-2)×(-2) = (-2)4
- (2×2×2×2) = -24
温习故知
1、举例说明乘法与乘方的关系,混合运算时,顺序是怎样的。
-2
2
4
4
问题一:根据乘方的意义填空(结果写成幂的形式) 。
问题二:观察左右两边,底数、指数各有什么关系?
问题三:得出你的猜想,并尝试证明你的猜想是否正确。
(1). 23 × 24 =(2 ×2×2)×(2×2×2×2)= 2 ( 3+4 ) =2( 7 )
(2).(—)3×(—)4=( × × )×( × × × )= (—)( ) = (—)( )
(3).0.53 × 0.54 =( × × )× ( × × × )= 0.5( ) =0.5( )
(4).(-3)3 ×(-3)4 =[ × × ]× [ × × × ]=(-3) ( ) =(-3) ( )
(5). a3 · a4 =( · · ) · ( · · · ) = a ( ) = a ( )
(7).(a+b)3×(a+b)4=[ × × ]× [ × × × ]=(a+b)( ) =(a+b)( )
探索新知
2
3
2
3
2
3
(6).(mn)3×(mn)4=[ × × ]× [ × × × ]=(mn) ( ) =(mn) ( )
边思考边解答呦!
2
3
问题一:根据乘方的意义填空(结果写成幂的形式) 。
(1). 23 × 24 = 2 ( )
(2). 0.53 × 0.54 =0.5 ( )
(3).(—)3 × (—)4 =(— ) ( )
(4).(-3)3 × (-3)4 = (-3) ( )
(5). a3 · a4 = a ( )
(6).(mn)3×(mn)4 =(mn)( )
(7).(a+b)3×(a+b)4=(a+b)( )
3+4
猜想: am · an= (m、n都是正整数)
3+4
3+4
3+4
3+4
探索新知
2
3
2
3
2
3
3+4
问题二:观察左右两边,发现底数、指数各有什么规律?
问题三:得出你的猜想,并尝试证明。
3+4
am · an =
=am+n
= aa…a
(m+n)个a
m个a
(aa…a )
n个a
(aa…a)
am · an= (m、n都是正整数)
am+n
(乘法结合律)
(乘方的意义)
归纳、证明
证明:
获得新知
am · an =
同底数幂相乘,
底数 ,指数 。
不变
相加
同底数幂的乘法性质:
am+n (m、n都是正整数)
注意事项:
1.条件:①底数相同,②乘法运算。
2.结果:①底数不变, ②将指数相加。
如:43×45=
43+5
=48
1016 ×103
= 1019
=(10×10×‥‥‥×10)×(10×10×10)
=( 10×10×‥‥‥×10 )
19个
= 1016+3
简化运算,体验了公式的简洁美!
应用新知解决问题
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数)
想一想: 当三个或三个以上同底数幂相乘时,是否也具有这一
性质呢?怎样用公式表示?
如 am · an · ap ?
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数)
公式的推广
例1 计算,结果用幂的形式表示:
(1)x2·x5; (2)a·a6;
(3)(-2)×(-2)4×(-2)3;(4)xm·x3m+1
a=a1
同底数幂的乘法性质:am·an =am+n (m、n都是正整数)
典型例题
1、计算:
(1)105×106=_____; (2)a7·a3=_______;
(3)x5·x7=_______; (4)(-b)3·(-b)2=__________.
2、判断下面的计算对不对?如果不对,应当怎样改正.
(1)b3·b3=2b3
(2)b3+b3=b6
(3)a·a5·a3=a8
(4)(-x)4·(-x)4=(-x)16
1011
a10
x12
(-b)5
=-b5
×
×
×
×
b6
2b3
=x8
a9
(-x)8
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数)
基础训练(抢答)
常见变形:(-a)2=a2, (-a)3=-a3
3、计算结果用幂的形式表示:
(1)(- —) ×(- —)2 × (- —)3 (2)y3×(-y)2
(3)(a+b)4·(a+b)7 (4)2m×2n×8
同底数幂的乘法性质:am·an =am+n (m、n都是正整数)
典型计算
1
3
1
3
1
3
4、判断下面的说法是否正确,如果正确请说明理由,如果不正确请举出反例:
两个幂相乘,如果底数不同就一定不能用性质计算。
请计算:(x-y)2·(y-x)5.
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数)
进阶练习
方法总结:
(1)当底数不同的幂相乘时,化为同底数的幂进行计算;
(2)当底数互为相反数的幂相乘时,根据幂的符号规律,可把不
同底数的幂化成同底数的幂相乘.
,n为偶数
,n为奇数
(a-b)n=
(b-a)n
-(b-a)n
常见变形:(-a)2=a2, (-a)3=-a3 ;
5、2022年4月16日,搭载“太空三人组”的神州十三号载人飞船结束了6个月的“太空出差”。已知神舟飞船在轨道上运行的速度大约为7.8 × 103米/秒,接近第一宇宙速度,那么这半年(大约1.6 × 107秒 )飞行了多少路程
实际应用
解:(7.8×103)×(1.6×107 )
=(7.8 × 1.6)×(103×107)
=12.48× 1010
答:太空三人组这半年共飞行了 1.248× 1011 米。
=1.248× 1011 (米)
【想一想】am+n可以写成哪两个因式的积?
公式的逆用
am+n=am·an
【填一填】若xm=3,xn=2,那么,
(1)xm+n= × = × = ;
(2)x2m= × = × =_ ;
(3)x2m+n= × = × = .
xm
xn
6
3
2
xm
xm
3
3
9
x2m
xn
9
2
18
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数)
=( ) × ( )
x10
【试一试】
6、 (1)若xa=3,xb=4,求xa+b的值.
(2)已知23x+2=32,求x的值;
方法总结:
(1) 逆用同底数幂的乘法性质,将所求代数式转化为几个已知因式的乘积的形式,然后再求值.
(2) 将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
拓展延伸
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数);逆用: am+n = am·an(m、n都是正整数)
通过对本节课的学习,
你有哪些收获呢?
同底数幂的乘法
性质
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用公式
常见变形:(-a)2n=a2n, (-a)2n+1=-a2n+1,
底数相同时
底数不相同时
先变成同底数再应用公式
课堂小结
am·an=am+n (m,n都是正整数)
,n为偶数
,n为奇数
(a-b)n=
(b-a)n
-(b-a)n
1.下列各式的结果等于26的是( )
A.2+25 B.2·25 C.23·25 D.0.22·0.24
2.下列计算结果正确的是( )
A.a3·a3=a9 B.m2·n2=mn4 C.xm·x3=x3m D.y·yn=yn+1
3.计算:(1)xn+1·x2n=_______;(2)(a-b)2·(a-b)3=_______;
(3)-a4·(-a)2=_____;(4)y4·y3·y2·y =_______.
4.填空:
(1)x·x2·x( )=x7;(2)xm·( )=x3m;(3)8×4=2x,则x=( )
B
D
4
5
x2m
-a6
y10
变式训练、自我检验
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数);逆用: am+n = am·an(m、n都是正整数)
x3n+1
(a-b)5
(2 )=
(a )=
(a )=
(a )=
3
3
4
4
m
4
n
m
1、必做题目:课本第96页练习(2)(4),习题14.1第1.(1)(2)题。
2、开放性题目:请给你的同桌用2、3、a、b(a、b为正整数)编计算题。要求如下:(1)所编题目为同底数幂乘法计算题;
(2)以上字母或者数字最多用两次。
3、探究题目:用同底数幂相乘的运算法则计算并观察底数和指数的变化规律。(选做)
课后作业与探究
同底数幂的乘法的性质:am·an =am+n (m、n都是正整数);逆用: am+n = am·an(m、n都是正整数)
