1.6实数(1) 课件(共31张PPT)
文档属性
| 名称 | 1.6实数(1) 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 00:00:00 | ||
图片预览










文档简介
课时1
实数
一般地,如果一个数的立方等于 a,那么这个数叫做 a 的立方根或三次方根.这就是说,如果 x3=a,那么 x 叫做 a 的立方根.
求一个数的立方根的运算叫做开立方.开立方与立方互为逆运算,可以利用开立方求一个数的立方根.
知识回顾
1.了解实数的意义,并能将实数按要求进行准确的分类.
3.了解实数和数轴上的点一一对应,能用数轴上的点表示无理数.
2.熟练掌握实数大小的比较方法.
学习目标
我们知道有理数包括整数和分数,请把下列分数写成小数的形式,你有什么发现?
52 -35 274 119 911
?
52 = 2.5 -35 = -0.6 274 = 6.75 119 = 1.2 911 = 0.81
?
?
? ?
知识点1:实数的概念和分类
新知探究
它们都可以写成有限小数或无限循环小数的形式.
事实上,如果把整数看成小数点后是 0 的小数,那么任何一个有理数都可以写成有限小数或无限循环小数的形式.反过来,任何有限小数或无限循环小数也都是有理数.
整数能写成小数的形式吗?
整数可以看成是小数点后是0的小数.
所有的数都可以写成有限小数或无限循环小数的形式吗?
π=3.1415926535897932384626…
1.01001000100001…(两个1之间依次多一个0)
不是. 如:
2=1.41421356…
?
35=1.70997594…
?
无限不循环小数叫做无理数.
有理数和无理数统称为实数.
注意:1.无理数都是无限小数,但无限小数不一定是无理数,只有无限不循环小数才是无理数.
2.某些数的平方根或立方根是无理数,但带根号的数不一定都是无理数.
常见的无理数的形式:
(1)开方开不尽的数的方根,如:3,35等;
(2) π 及化简后含 π 的数,如:π2,π+1等;
(3)具有特殊结构的数,如:0.3030030003…(相邻两个 3之间依次多一个 0 ).
?
像有理数一样,无理数也有正负之分.例如,3是正无理数,?3是负无理数.
?
无理数与有理数的区别
(1)任何有理数都能化成分数(整数可以看成分母是1的分数),无理数不能化成分数.
(2)任何一个有理数都可以化成有限小数(把整数看成小数点后是0的小数)或无限循环小数,无理数是无限不循环小数.
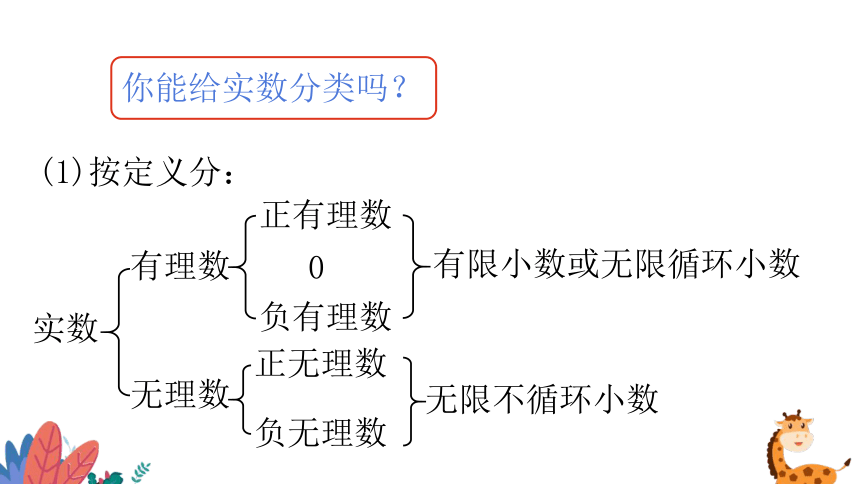
(1)按定义分:
你能给实数分类吗?
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
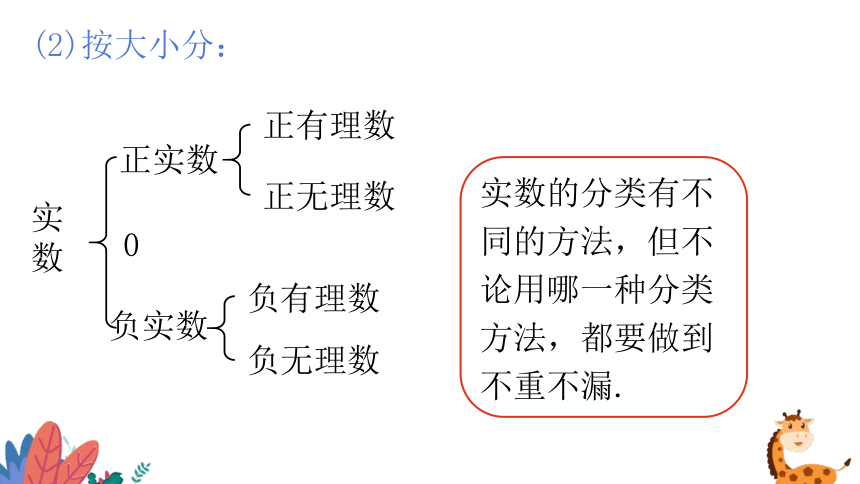
(2)按大小分:
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
实数的分类有不同的方法,但不论用哪一种分类方法,都要做到不重不漏.
把下列各数填在相应的大括号内.
正实数:{ …};
有理数:{ …} ;
无理数:{ …}.
π4,227,6,64
?
?6,?23,??3,227,?0.4,0,64,?312564
?
π4,6
?
?6,π4,?23,??3,227,?0.4,6,0,64,?312564.
?
跟踪训练
新知探究
非负整数:{ …};
整数:{ …};
负分数:{ …};
?0,64
?
?6,???3,0,64
?
??23,?0.4,??312564
?
把下列各数填在相应的大括号内.
?6,π4,?23,??3,227,?0.4,6,0,64,?312564.
?
感悟新知
把下列各数填入相应的集合内
-????????, -????, ????????, ???????? , -????-???? ,0, -π, - ???????????????? , -4.????0????,3.1010010001…(每相邻两个 1 之间 0 的个数逐次加 1) .
无理数集合:{ …} .
分数集合:{ …} .
负实数集合:{ …} .
?
新知探究
跟踪训练
感悟新知
解题秘方:根据有理数、无理数等概念进行分类时,应注意先把一些数进行化简,再进行判断,如 - ????-???? =2.
?
感悟新知
解: 无理数集合:{ -???? , ?????????, - π,3.101 001 000 1… (每相邻两个 1 之间 0 的个数逐次加 1 ) ,… . }
分数集合: {- ???????? ,????????, - ???????????????? , - 4. ????0?????,… . }
负实数集合: {- ???????? , - ???? , - π, - ???????????????? ,
- 4. ????0?????,… . }
?
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点 O',点 O' 对应的数是多少?
知识点2:实数与数轴上的点
新知探究
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
O'
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?
从图中可以看出,OO' 的长是这个圆的周长 π,所以点 O' 对应的数是 π.
这样,无理数 π 可以用数轴上的点表示出来.
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
O'
把两个边长为1的小正方形通过剪、拼,得到一个大正方形,大正方形的边长为 2 ,从而说明边长为1的小正方形的对角线长为?2.
?
你能在数轴上表示出 2 和 ?2 吗?
?
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一个点都表示一个实数.
-2
-1
0
1
2
2
?
?2
?
实数和数轴上的点一 一对应
2
?
与有理数一样,实数也可以比较大小.
对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大.
1.正实数大于0,负实数小于0,正实数大于一切负实数;
2. 两个负实数比较大小,绝对值大的反而小.
不用计算器, 5 与 2 比较哪个大?与 3 比较呢?
?
5 ,2可以分别看作是面积为5,4的正方形的边长,可以推断:面积较大的正方形,它的边长也比较大,因此 5>2 .
?
因为5<9,所以5<3.
?
1.下列说法正确的有( )
①数轴上任意一点都表示一个有理数;
②任意一个无理数都可以用数轴上的一个点来表示;
③任意一个实数都可以用数轴上的一个点来表示;
④有理数与数轴上的点一 一对应.
B
A.1个 B.2个 C.3 D.4个
跟踪训练
新知探究
实数
实数
感悟新知
1、用“<”连接下列各数: - ???????? , ????, - 2???? ,2.5,0.
?
解题秘方:比较一组实数的大小和比较一组有理数的大小一样,可先将这些数在数轴上表示出来,然后根据“数轴上右边的点表示的数总比左边的点表示的数大”求解 .
新知探究
跟踪训练
感悟新知
解: 将各数的大致位置在数轴上表示出来,如图 2-6-1.
由图可知, -2 ???? <-???????? <0< ???? <2.5.
?
1. 已知a,b两数在数轴上对应的点的位置如图所示,则下列结论中正确的是( )
A.a>b B.|a|<|b|
C.ab>0 D.-a>b
返回
D
随堂练习
2. 实数 +1在如图所示的数轴上的对应点可能是( )
A.A点 B.B点
C. C点 D.D点
D
3.比较 32?1 与 1+22 的大小.
?
解:32?1?1+22=32?1?1?22 =2?2.
∵2<4,
∴2<4,即2<2,
∴2?2<0,
∴32?1?1+22<0,
∴32?1 < 1+22 .
?
1.实数 a,b 在数轴上的对应点的位置如图所示.下列结论正确的是( )
A. a>b B. a> -b C. -a>b D. -aC
拓展提升
2.比较3,10,325的大小( )
A. 3<10<325?
B. 3<325<10
C. 325<3<10?
D. 10<325<3
?
C
10>9=3
?
325<327=3
?
3.设?x,y?是有理数,且?x,y?满足等式 x2+2y+2y=17-42?,求 x-y 的值.
?
解:∵ x,y 是有理数,且 x,y 满足等式 x2+2y+2y=17-42?,
∴ ????2+2????=17,????=?4, 解得 ????=5,????=?4, 或 ????=?5,????=?4,
∴ 当 x=5,y=-4 时,x-y=5-(-4)=9,
当 x=-5,y=-4 时,x-y=-5-(-4)=-1.
实数
一般地,如果一个数的立方等于 a,那么这个数叫做 a 的立方根或三次方根.这就是说,如果 x3=a,那么 x 叫做 a 的立方根.
求一个数的立方根的运算叫做开立方.开立方与立方互为逆运算,可以利用开立方求一个数的立方根.
知识回顾
1.了解实数的意义,并能将实数按要求进行准确的分类.
3.了解实数和数轴上的点一一对应,能用数轴上的点表示无理数.
2.熟练掌握实数大小的比较方法.
学习目标
我们知道有理数包括整数和分数,请把下列分数写成小数的形式,你有什么发现?
52 -35 274 119 911
?
52 = 2.5 -35 = -0.6 274 = 6.75 119 = 1.2 911 = 0.81
?
?
? ?
知识点1:实数的概念和分类
新知探究
它们都可以写成有限小数或无限循环小数的形式.
事实上,如果把整数看成小数点后是 0 的小数,那么任何一个有理数都可以写成有限小数或无限循环小数的形式.反过来,任何有限小数或无限循环小数也都是有理数.
整数能写成小数的形式吗?
整数可以看成是小数点后是0的小数.
所有的数都可以写成有限小数或无限循环小数的形式吗?
π=3.1415926535897932384626…
1.01001000100001…(两个1之间依次多一个0)
不是. 如:
2=1.41421356…
?
35=1.70997594…
?
无限不循环小数叫做无理数.
有理数和无理数统称为实数.
注意:1.无理数都是无限小数,但无限小数不一定是无理数,只有无限不循环小数才是无理数.
2.某些数的平方根或立方根是无理数,但带根号的数不一定都是无理数.
常见的无理数的形式:
(1)开方开不尽的数的方根,如:3,35等;
(2) π 及化简后含 π 的数,如:π2,π+1等;
(3)具有特殊结构的数,如:0.3030030003…(相邻两个 3之间依次多一个 0 ).
?
像有理数一样,无理数也有正负之分.例如,3是正无理数,?3是负无理数.
?
无理数与有理数的区别
(1)任何有理数都能化成分数(整数可以看成分母是1的分数),无理数不能化成分数.
(2)任何一个有理数都可以化成有限小数(把整数看成小数点后是0的小数)或无限循环小数,无理数是无限不循环小数.
(1)按定义分:
你能给实数分类吗?
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
(2)按大小分:
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
实数的分类有不同的方法,但不论用哪一种分类方法,都要做到不重不漏.
把下列各数填在相应的大括号内.
正实数:{ …};
有理数:{ …} ;
无理数:{ …}.
π4,227,6,64
?
?6,?23,??3,227,?0.4,0,64,?312564
?
π4,6
?
?6,π4,?23,??3,227,?0.4,6,0,64,?312564.
?
跟踪训练
新知探究
非负整数:{ …};
整数:{ …};
负分数:{ …};
?0,64
?
?6,???3,0,64
?
??23,?0.4,??312564
?
把下列各数填在相应的大括号内.
?6,π4,?23,??3,227,?0.4,6,0,64,?312564.
?
感悟新知
把下列各数填入相应的集合内
-????????, -????, ????????, ???????? , -????-???? ,0, -π, - ???????????????? , -4.????0????,3.1010010001…(每相邻两个 1 之间 0 的个数逐次加 1) .
无理数集合:{ …} .
分数集合:{ …} .
负实数集合:{ …} .
?
新知探究
跟踪训练
感悟新知
解题秘方:根据有理数、无理数等概念进行分类时,应注意先把一些数进行化简,再进行判断,如 - ????-???? =2.
?
感悟新知
解: 无理数集合:{ -???? , ?????????, - π,3.101 001 000 1… (每相邻两个 1 之间 0 的个数逐次加 1 ) ,… . }
分数集合: {- ???????? ,????????, - ???????????????? , - 4. ????0?????,… . }
负实数集合: {- ???????? , - ???? , - π, - ???????????????? ,
- 4. ????0?????,… . }
?
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点 O',点 O' 对应的数是多少?
知识点2:实数与数轴上的点
新知探究
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
O'
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?
从图中可以看出,OO' 的长是这个圆的周长 π,所以点 O' 对应的数是 π.
这样,无理数 π 可以用数轴上的点表示出来.
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
O'
把两个边长为1的小正方形通过剪、拼,得到一个大正方形,大正方形的边长为 2 ,从而说明边长为1的小正方形的对角线长为?2.
?
你能在数轴上表示出 2 和 ?2 吗?
?
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一个点都表示一个实数.
-2
-1
0
1
2
2
?
?2
?
实数和数轴上的点一 一对应
2
?
与有理数一样,实数也可以比较大小.
对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大.
1.正实数大于0,负实数小于0,正实数大于一切负实数;
2. 两个负实数比较大小,绝对值大的反而小.
不用计算器, 5 与 2 比较哪个大?与 3 比较呢?
?
5 ,2可以分别看作是面积为5,4的正方形的边长,可以推断:面积较大的正方形,它的边长也比较大,因此 5>2 .
?
因为5<9,所以5<3.
?
1.下列说法正确的有( )
①数轴上任意一点都表示一个有理数;
②任意一个无理数都可以用数轴上的一个点来表示;
③任意一个实数都可以用数轴上的一个点来表示;
④有理数与数轴上的点一 一对应.
B
A.1个 B.2个 C.3 D.4个
跟踪训练
新知探究
实数
实数
感悟新知
1、用“<”连接下列各数: - ???????? , ????, - 2???? ,2.5,0.
?
解题秘方:比较一组实数的大小和比较一组有理数的大小一样,可先将这些数在数轴上表示出来,然后根据“数轴上右边的点表示的数总比左边的点表示的数大”求解 .
新知探究
跟踪训练
感悟新知
解: 将各数的大致位置在数轴上表示出来,如图 2-6-1.
由图可知, -2 ???? <-???????? <0< ???? <2.5.
?
1. 已知a,b两数在数轴上对应的点的位置如图所示,则下列结论中正确的是( )
A.a>b B.|a|<|b|
C.ab>0 D.-a>b
返回
D
随堂练习
2. 实数 +1在如图所示的数轴上的对应点可能是( )
A.A点 B.B点
C. C点 D.D点
D
3.比较 32?1 与 1+22 的大小.
?
解:32?1?1+22=32?1?1?22 =2?2.
∵2<4,
∴2<4,即2<2,
∴2?2<0,
∴32?1?1+22<0,
∴32?1 < 1+22 .
?
1.实数 a,b 在数轴上的对应点的位置如图所示.下列结论正确的是( )
A. a>b B. a> -b C. -a>b D. -aC
拓展提升
2.比较3,10,325的大小( )
A. 3<10<325?
B. 3<325<10
C. 325<3<10?
D. 10<325<3
?
C
10>9=3
?
325<327=3
?
3.设?x,y?是有理数,且?x,y?满足等式 x2+2y+2y=17-42?,求 x-y 的值.
?
解:∵ x,y 是有理数,且 x,y 满足等式 x2+2y+2y=17-42?,
∴ ????2+2????=17,????=?4, 解得 ????=5,????=?4, 或 ????=?5,????=?4,
∴ 当 x=5,y=-4 时,x-y=5-(-4)=9,
当 x=-5,y=-4 时,x-y=-5-(-4)=-1.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
