圆的标准方程[上学期]
图片预览


文档简介
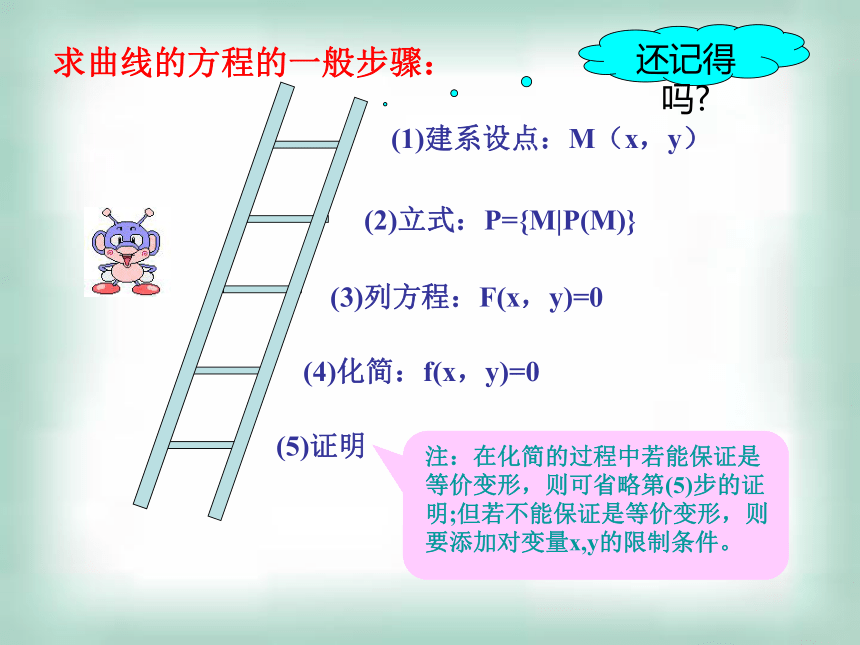
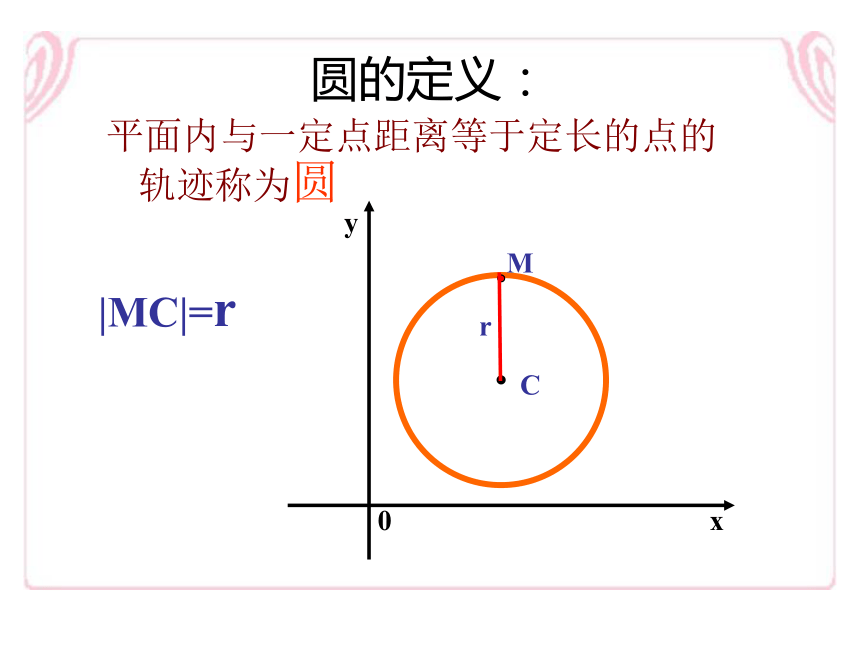
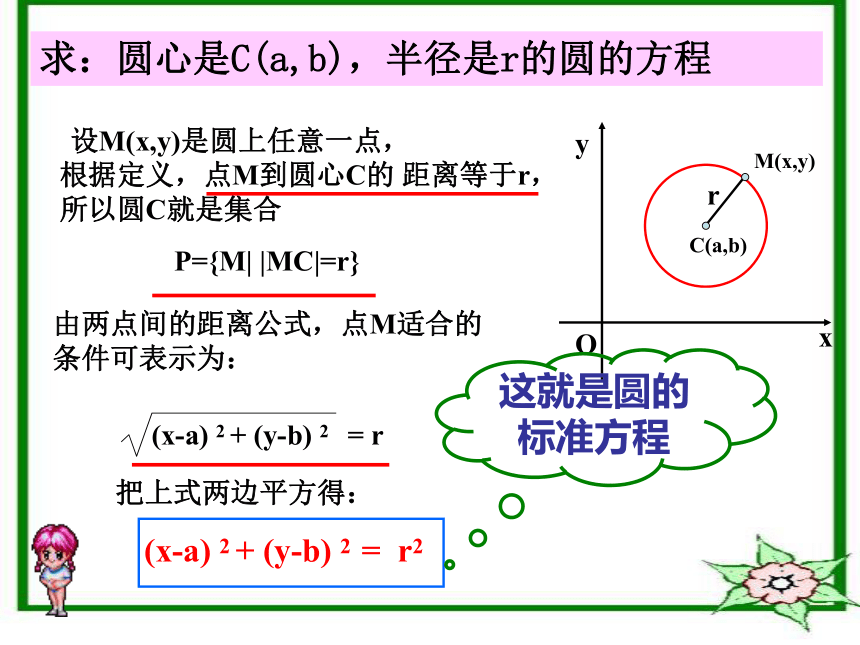
课件15张PPT。课件制作人:龙南中学 段文琼课题:圆的标准方程复习引入圆的方程例题分析课堂小结布置作业圆的标准方程求曲线的方程的一般步骤:(3)列方程:F(x,y)=0(4)化简:f(x,y)=0(5)证明(1)建系设点:M(x,y)(2)立式:P={M|P(M)}还记得吗?圆的定义:平面内与一定点距离等于定长的点的轨迹称为圆Mr|MC|=r求:圆心是C(a,b),半径是r的圆的方程设M(x,y)是圆上任意一点,这就是圆的标准方程其实并不难!
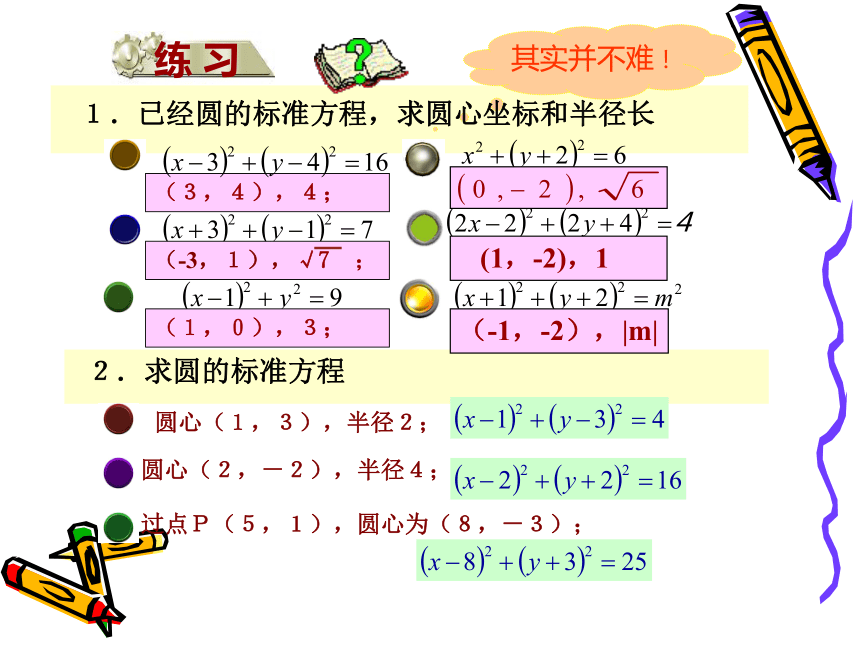
1.已经圆的标准方程,求圆心坐标和半径长2.求圆的标准方程圆心(1,3),半径2;圆心(2,-2),半径4;过点P(5,1),圆心为(8,-3);(3,4),4;(1,0),3;练 习 (1,-2),1(-1,-2),|m|设点到圆心的距离为d,圆半径为r:(2) d=r(3) d>r(1) d<r点与圆的位置关系点在圆上点在圆内点在圆外例1(1)求以C(1,3)为圆心,并且和直线3x-4y-7=0 相切的圆的方程。因为圆C和直线3x-4y-7=0相切,
所以圆心C到这条直线的距离等于半径r , 解:设所求圆的方程为:
(x-1)2+(y-3)2=r2
(2)过两点A(1,-1),B(-1,1)且圆心在直线x+y-2=0上的圆的方程.KAB=-1,则Kl=1AB中点坐标为(0,0),
l方程为:x-y=0ABx+y-2=0lr=2圆的方程为:(x-1)2+(y-1)2=4解:如图作AB的中垂线l,例2 已知圆的方程是 ,求经过圆上一点 的切线的方程。当点M在坐标轴上时,可以验证,上面方程同样适用.过圆 x2+y2=r2 上一点M(x0,y0) 的切线的方程为:过圆(x-a)2+(y-b)2=r2 上一点M(x0,y0) 的切线方程为: 例3:如图是某圆拱桥的一孔圆拱的示意图.该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01m)解:建立如图所示的坐标系,设圆心坐标是(0,b)圆的半径是r ,则圆的方程是
x2+(y-b)2=r2 。答:支柱A2P2的长度约为3.86m。1.求圆的方程的两种方法:
(1)待定系数法,确定a,b,r;
(2)轨迹法,求曲线方程的一般方法.记住了吗?小结2.过圆 x2+y2=r2 上一点M(x0,y0) 的切线的方程为:过圆(x-a)2+(y-b)2=r2 上一点M(x0,y0) 的切线方程为: x0x +y0 y = r2(x0-a)(x-a)+(y0-b)(y-b)=r2 思考题(2)过点A(3,2),圆心在直线y=2x上,且与直线y=2x+5相切.(1)圆心为 C(3,-5),并且与直线x-7y+2=0相切;1.求下列条件所决定的圆的方程:谢谢指导!
1.已经圆的标准方程,求圆心坐标和半径长2.求圆的标准方程圆心(1,3),半径2;圆心(2,-2),半径4;过点P(5,1),圆心为(8,-3);(3,4),4;(1,0),3;练 习 (1,-2),1(-1,-2),|m|设点到圆心的距离为d,圆半径为r:(2) d=r(3) d>r(1) d<r点与圆的位置关系点在圆上点在圆内点在圆外例1(1)求以C(1,3)为圆心,并且和直线3x-4y-7=0 相切的圆的方程。因为圆C和直线3x-4y-7=0相切,
所以圆心C到这条直线的距离等于半径r , 解:设所求圆的方程为:
(x-1)2+(y-3)2=r2
(2)过两点A(1,-1),B(-1,1)且圆心在直线x+y-2=0上的圆的方程.KAB=-1,则Kl=1AB中点坐标为(0,0),
l方程为:x-y=0ABx+y-2=0lr=2圆的方程为:(x-1)2+(y-1)2=4解:如图作AB的中垂线l,例2 已知圆的方程是 ,求经过圆上一点 的切线的方程。当点M在坐标轴上时,可以验证,上面方程同样适用.过圆 x2+y2=r2 上一点M(x0,y0) 的切线的方程为:过圆(x-a)2+(y-b)2=r2 上一点M(x0,y0) 的切线方程为: 例3:如图是某圆拱桥的一孔圆拱的示意图.该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01m)解:建立如图所示的坐标系,设圆心坐标是(0,b)圆的半径是r ,则圆的方程是
x2+(y-b)2=r2 。答:支柱A2P2的长度约为3.86m。1.求圆的方程的两种方法:
(1)待定系数法,确定a,b,r;
(2)轨迹法,求曲线方程的一般方法.记住了吗?小结2.过圆 x2+y2=r2 上一点M(x0,y0) 的切线的方程为:过圆(x-a)2+(y-b)2=r2 上一点M(x0,y0) 的切线方程为: x0x +y0 y = r2(x0-a)(x-a)+(y0-b)(y-b)=r2 思考题(2)过点A(3,2),圆心在直线y=2x上,且与直线y=2x+5相切.(1)圆心为 C(3,-5),并且与直线x-7y+2=0相切;1.求下列条件所决定的圆的方程:谢谢指导!
