圆的标准方程[上学期]
图片预览





文档简介
(共18张PPT)
*
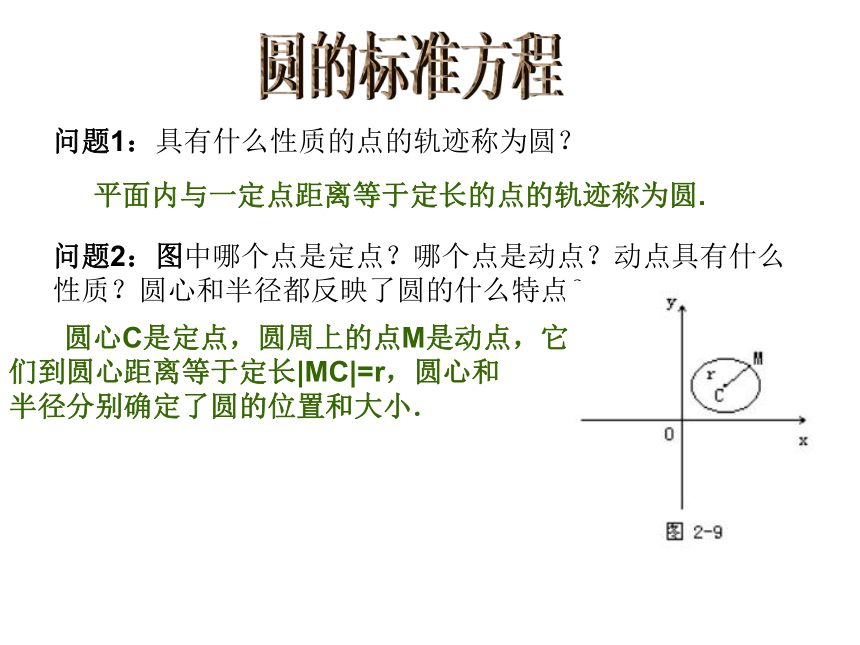
问题1:具有什么性质的点的轨迹称为圆?
平面内与一定点距离等于定长的点的轨迹称为圆.
问题2:图中哪个点是定点?哪个点是动点?动点具有什么性质?圆心和半径都反映了圆的什么特点?
圆心C是定点,圆周上的点M是动点,它
们到圆心距离等于定长|MC|=r,圆心和
半径分别确定了圆的位置和大小.
下面我们用求曲线方程的一般步骤来建立圆的标准方程.
解:设M(x,y)是圆上任意一点,
x
y
O
.
r
M
根据圆的定义|MC|=r
C
由两点间距离公式,得
①
把①式两边平方,得
说明:
1.特点:明确给出了圆心和
半径。
2.确定圆的方程必须具备三个
独立的条件。
练习 1.写出下列各圆的方程:
(1)圆心在圆点,半径是3;
(3)经过点P(5,1),圆心在点C(8,-3)
(2)圆心在点C(3,4),半径是 ;
练习2.写出下列各圆的圆心坐标和半径
(1)
(2)
(3)
(-1,2) 3
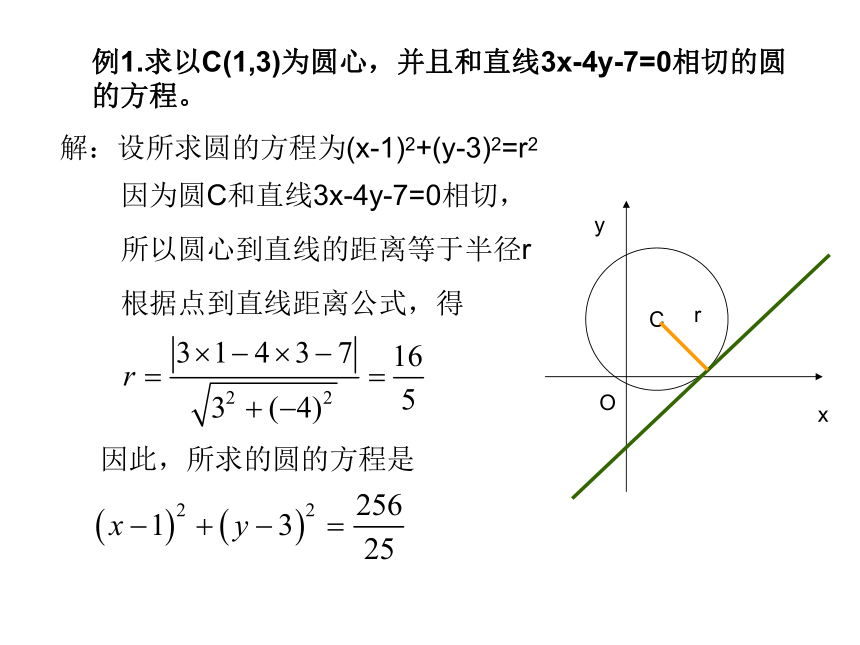
例1.求以C(1,3)为圆心,并且和直线3x-4y-7=0相切的圆
的方程。
解:设所求圆的方程为(x-1)2+(y-3)2=r2
因为圆C和直线3x-4y-7=0相切,
所以圆心到直线的距离等于半径r
C
x
y
O
r
根据点到直线距离公式,得
因此,所求的圆的方程是
练习3.已知一个圆的圆心在原点,并与直线4x+3y-70=0
相切,求圆的方程。
例2.已知圆的方程是x2+y2=r2,求经过圆上一点M(x0,y0)
的切线的方程。
解:如图,
x
y
O
.
M(x0,y0)
设切线的斜率为k
半径OM的斜率为k1,
因为圆的切线垂直于过切点的
半径,于是
经过点M的切线方程是
整理得,x0x+y0y=x02+y02
因为点M(x0,y0)在圆上,所以x02+y02=r2
所求切线方程是x0x+y0y=r2
当点M在坐标轴上时,可以验证上面方程同样适用。
1.圆的方程是x2+y2=r2,经过圆上一点M(x0,y0)的切线的方程是
2.圆的方程为(x-a)2+(y-b)2=r2上的点的切线方程是(x-a)( -a)+(y-b)( -b)=r2
x0x+y0y=r2
y0
例2 已知圆的方程是 ,求经过圆上一点
的切线的方程。
P(x , y )
由勾股定理:|OM|2+|MP|2=|OP|2
解法二(利用平面几何知识):
在直角三角形OMP中
y
x
O
x0x +y0 y = r2
P(x , y )
y
x
O
例2 已知圆的方程是 ,求经过圆上一点
的切线的方程。
解法三(利用平面向量知识):
OM MP= 0
OM MP
x0x +y0 y = r2
x2 + y2 = r2
练习4.写出过圆x2+y2=10上一点M 的切线的方程
练习5.已知圆的方程是x2+y2=1,求
(1)斜率等于1的切线的方程;
(2)在y轴上截距是 的切线的方程。
所以切线方程为:y = x±
2
提示:设切线方程为 y=x+b ,由圆心到切线的距离等于半径1,得: |b|
12+(-1)2
=1 解得b=±
2
2
(2)在y轴上截距是 的切线方程。
y = ± x+
2
例3 过点A(1,-1),B(-1,1)且圆心在直线
X+y-2=0上的圆的方程
圆心的性质:
1,圆心在过切点且与切线垂直的直线上
2,圆心在弦的中垂线上
3,两圆内切或外切时,切点与两圆圆心三点共线
例4 求与x轴切于点(5,0)并在y轴上
截得弦长为10的圆的方程.
小结:
直线与圆相交,求弦长或与弦长有关的问题
到垂径定理,和利用半弦长,弦心距,及
半径组成的直角三角形
小结
(1) 圆心为C(a,b),半径为r 的圆的标准方程为
(x-a) 2 + (y-b) 2 = r2
当圆心在原点时 a=b=0,圆的标准方程为:
x2 + y2 = r2
(2) 由于圆的标准方程中含有 a , b , r 三个参数,因此必须具备三个独立的条件才能确定圆;对于由已知条件容易求得圆心坐标和圆的半径或需利用圆心坐标列方程的问题一般采用圆的标准方程。
(3) 注意圆的平面几何知识的运用以及应用圆的方程解决实际问题。
作业:
书P81习题7.6___4
*
问题1:具有什么性质的点的轨迹称为圆?
平面内与一定点距离等于定长的点的轨迹称为圆.
问题2:图中哪个点是定点?哪个点是动点?动点具有什么性质?圆心和半径都反映了圆的什么特点?
圆心C是定点,圆周上的点M是动点,它
们到圆心距离等于定长|MC|=r,圆心和
半径分别确定了圆的位置和大小.
下面我们用求曲线方程的一般步骤来建立圆的标准方程.
解:设M(x,y)是圆上任意一点,
x
y
O
.
r
M
根据圆的定义|MC|=r
C
由两点间距离公式,得
①
把①式两边平方,得
说明:
1.特点:明确给出了圆心和
半径。
2.确定圆的方程必须具备三个
独立的条件。
练习 1.写出下列各圆的方程:
(1)圆心在圆点,半径是3;
(3)经过点P(5,1),圆心在点C(8,-3)
(2)圆心在点C(3,4),半径是 ;
练习2.写出下列各圆的圆心坐标和半径
(1)
(2)
(3)
(-1,2) 3
例1.求以C(1,3)为圆心,并且和直线3x-4y-7=0相切的圆
的方程。
解:设所求圆的方程为(x-1)2+(y-3)2=r2
因为圆C和直线3x-4y-7=0相切,
所以圆心到直线的距离等于半径r
C
x
y
O
r
根据点到直线距离公式,得
因此,所求的圆的方程是
练习3.已知一个圆的圆心在原点,并与直线4x+3y-70=0
相切,求圆的方程。
例2.已知圆的方程是x2+y2=r2,求经过圆上一点M(x0,y0)
的切线的方程。
解:如图,
x
y
O
.
M(x0,y0)
设切线的斜率为k
半径OM的斜率为k1,
因为圆的切线垂直于过切点的
半径,于是
经过点M的切线方程是
整理得,x0x+y0y=x02+y02
因为点M(x0,y0)在圆上,所以x02+y02=r2
所求切线方程是x0x+y0y=r2
当点M在坐标轴上时,可以验证上面方程同样适用。
1.圆的方程是x2+y2=r2,经过圆上一点M(x0,y0)的切线的方程是
2.圆的方程为(x-a)2+(y-b)2=r2上的点的切线方程是(x-a)( -a)+(y-b)( -b)=r2
x0x+y0y=r2
y0
例2 已知圆的方程是 ,求经过圆上一点
的切线的方程。
P(x , y )
由勾股定理:|OM|2+|MP|2=|OP|2
解法二(利用平面几何知识):
在直角三角形OMP中
y
x
O
x0x +y0 y = r2
P(x , y )
y
x
O
例2 已知圆的方程是 ,求经过圆上一点
的切线的方程。
解法三(利用平面向量知识):
OM MP= 0
OM MP
x0x +y0 y = r2
x2 + y2 = r2
练习4.写出过圆x2+y2=10上一点M 的切线的方程
练习5.已知圆的方程是x2+y2=1,求
(1)斜率等于1的切线的方程;
(2)在y轴上截距是 的切线的方程。
所以切线方程为:y = x±
2
提示:设切线方程为 y=x+b ,由圆心到切线的距离等于半径1,得: |b|
12+(-1)2
=1 解得b=±
2
2
(2)在y轴上截距是 的切线方程。
y = ± x+
2
例3 过点A(1,-1),B(-1,1)且圆心在直线
X+y-2=0上的圆的方程
圆心的性质:
1,圆心在过切点且与切线垂直的直线上
2,圆心在弦的中垂线上
3,两圆内切或外切时,切点与两圆圆心三点共线
例4 求与x轴切于点(5,0)并在y轴上
截得弦长为10的圆的方程.
小结:
直线与圆相交,求弦长或与弦长有关的问题
到垂径定理,和利用半弦长,弦心距,及
半径组成的直角三角形
小结
(1) 圆心为C(a,b),半径为r 的圆的标准方程为
(x-a) 2 + (y-b) 2 = r2
当圆心在原点时 a=b=0,圆的标准方程为:
x2 + y2 = r2
(2) 由于圆的标准方程中含有 a , b , r 三个参数,因此必须具备三个独立的条件才能确定圆;对于由已知条件容易求得圆心坐标和圆的半径或需利用圆心坐标列方程的问题一般采用圆的标准方程。
(3) 注意圆的平面几何知识的运用以及应用圆的方程解决实际问题。
作业:
书P81习题7.6___4
