全国人教版数学九年级上册课课练:24章 专题训练 圆中常用辅助线的作法(含答案解析)
文档属性
| 名称 | 全国人教版数学九年级上册课课练:24章 专题训练 圆中常用辅助线的作法(含答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 791.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-30 00:00:00 | ||
图片预览




文档简介
专题训练 圆中常用辅助线的作法
作法一 作半径或直径
①作半径(或直径):构造等腰三角形或直角三角形
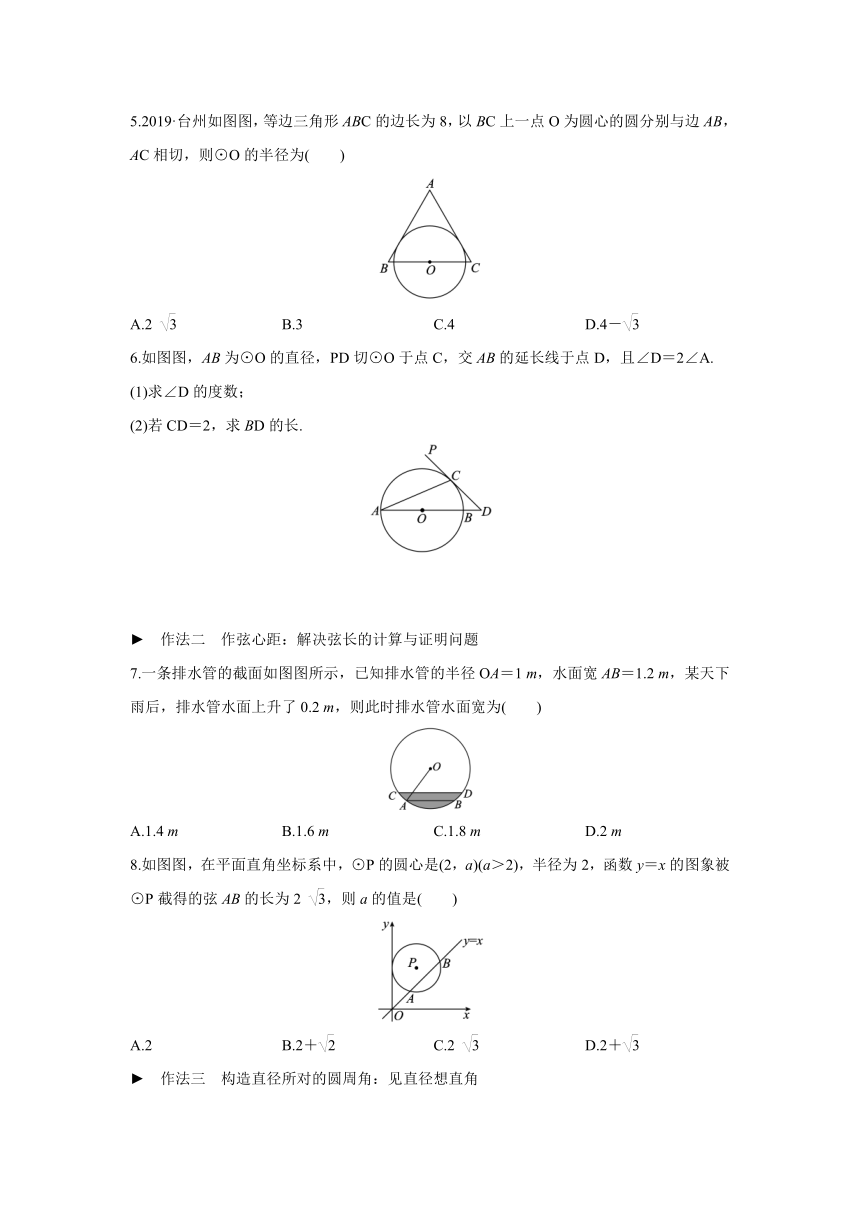
1.如图图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5.若P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
A.5 B. C.5 D.5
2.2019·绍兴如图图,△ABC内接于⊙O,∠B=65°,∠C=70°.若BC=2 ,则的长为( )
A.π B.π C.2π D.2 π
3.2020·攀枝花如图图,已知锐角三角形ABC内接于半径为2的⊙O,OD⊥BC于点D,∠BAC=60°,则OD=________.
②连接过切点的半径或直径:见切线,连切点,得垂直
4.2019·青岛如图图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为( )
A.π B.2π C.2 π D.4π
5.2019·台州如图图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为( )
A.2 B.3 C.4 D.4-
6.如图图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠A.
(1)求∠D的度数;
(2)若CD=2,求BD的长.
作法二 作弦心距:解决弦长的计算与证明问题
7.一条排水管的截面如图图所示,已知排水管的半径OA=1 m,水面宽AB=1.2 m,某天下雨后,排水管水面上升了0.2 m,则此时排水管水面宽为( )
A.1.4 m B.1.6 m C.1.8 m D.2 m
8.如图图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为2 ,则a的值是( )
A.2 B.2+ C.2 D.2+
作法三 构造直径所对的圆周角:见直径想直角
9.2020·泰安如图图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4 B.4 C. D.2
10.2019·绵阳如图图,AB是⊙O的直径,C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
作法四 判定直线与圆相切(作半径或作垂直)
①有交点 作半径,证垂直
11.如图图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆O交AC于点D,E为BC的中点,连接DE.
(1)求证:DE是半圆O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
12.如图图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.求证:直线DM是⊙O的切线.
②无交点 作垂直,证半径
13.如图图,△ABC是等边三角形,AO⊥BC,垂足为O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点.
(1)求证:AB与⊙O相切;
(2)若等边三角形ABC的边长是4,求线段BF的长.
答案
1.D 如图图图,连接OB,OA,
设OB与AP交于点D.由PB=AB可知=,从而可知OB⊥AP.运用“一条弧所对的圆周角等于它所对的圆心角的一半”及“同圆的半径相等”可知△OAB为等边三角形,在Rt△OAD中,运用“在直角三角形中,30°角所对的直角边等于斜边的一半”及勾股定理列方程可求得AD的长,从而可求出AP的长为5 .故选D.
2.A 在△ABC中,由三角形内角和定理,得∠A=180°-∠ABC-∠ACB=45°.
连接OB,OC,则∠BOC=2∠A=90°.
设圆的半径为r,由勾股定理,得r2+r2=(2 )2,解得r=2,所以的长为=π.
3.1 如图图图,连接OB,OC,
则易知∠BOC=2∠BAC=120°,由垂径定理可知∠BOD=∠BOC=60°,
则∠OBD=30°,∴OD=OB=1.
4.B 如图图图,连接CO,DO.
因为AC,BD分别与⊙O相切于点C,D,
所以∠ACO=∠BDO=90°.
又因为∠A=45°,
所以∠AOC=45°=∠A,所以CO=AC=4.
因为AC=BD,∠ACO=∠BDO,CO=DO,
所以△ACO≌△BDO,
所以∠DOB=∠AOC=45°,
所以∠DOC=180°-∠DOB-∠AOC=180°-45°-45°=90°,所以的长==2π.
故选B.
5.A 如图图图,设⊙O与AC的切点为E,连接AO,OE.
∵等边三角形ABC的边长为8,
∴AC=8,∠C=∠BAC=60°.
∵⊙O分别与边AB,AC相切,
∴∠OEC=90°,∠BAO=∠CAO=∠BAC=30°,
∴∠AOC=90°,
∴OC=AC=4.
在Rt△OCE中,∠OEC=90°,∠C=60°,
∴∠COE=30°,
∴CE=OC=2,∴OE=2 ,
∴⊙O的半径为2 .
6.解:(1)连接OC.
∵∠COD=2∠A,∠D=2∠A,
∴∠COD=∠D.
∵PD与⊙O相切于点C,
∴OC⊥PD,即∠OCD=90°,
∴∠D=×(180°-90°)=45°.
(2)由(1)可知∠COD=∠D,∴OC=CD=2.
由勾股定理,得OD==2 ,
∴BD=OD-OB=2 -2.
7.B 如图图图,过点O作OE⊥AB于点E,交CD于点F,连接OC.
∵AB=1.2 m,OE⊥AB,
∴AE=AB=0.6 m.
又∵OA=1 m,
∴由勾股定理,得OE=0.8 m.
∵排水管水面上升了0.2 m,
∴OF=0.8-0.2=0.6(m).
由题意可知CD∥AB.
∵OE⊥AB,∴OE⊥CD,
∴CF==0.8 m,CD=2CF,
∴CD=1.6 m.故选B.
8.B 如图图图,
连接PB,过点P作PC⊥AB于点C,过点P作横轴的垂线,垂足为E,交AB于点D,则PB=2,BC=.在Rt△PBC中,由勾股定理得PC=1.∵直线y=x平分第一象限的夹角,∴△PCD和△DEO都是等腰直角三角形,∴PD=,DE=OE=2,∴a=PE=2+.故选B.
9.B 连接CD,如图图图.
∵AB=BC,∠BAC=30°,
∴∠ACB=∠BAC=30°,
∴∠B=180°-30°-30°=120°,
∴∠D=180°-∠B=60°.
∵AD是直径,
∴∠ACD=90°,∴∠CAD=30°.
又∵AD=8,∴CD=AD=4,
∴AC===4 .
10.解:(1)证明:∵C为的中点,
∴=.
∵AB是⊙O的直径,且CF⊥AB,
∴=,∴=,
∴CD=BF.
在△BFG和△CDG中,
∴△BFG≌△CDG(AAS).
(2)解法一:如图图图①,连接OF.设⊙O的半径为r.
∵AB是⊙O的直径,
∴∠ADB=90°.
在Rt△ADB中,BD2=AB2-AD2,
即BD2=(2r)2-22.
在Rt△OEF中,OF2=OE2+EF2,
即EF2=r2-(r-2)2.
由(1)知==,
∴=,∴BD=CF,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2-22=4[r2-(r-2)2],
解得r=1(不合题意,舍去)或r=3,
∴BF2=EF2+BE2=32-(3-2)2+22=12,
∴BF=2 .
解法二:如图图图②,连接OC,交BD于点H.
∵C是的中点,
∴OC⊥BD,
∴DH=BH.
∵OA=OB,
∴OH=AD=1.
∵∠COE=∠BOH,∠OEC=∠OHB=90°,OC=OB,
∴△COE≌△BOH(AAS),
∴OE=OH=1,
∴OC=OB=OE+BE=3.
∵CF⊥AB,
∴CE=EF===2 ,
∴BF===2 .
11.解:(1)证明:如图图图,连接BD,OD,OE.
∵AB为半圆O的直径,
∴∠ADB=∠BDC=90°.
在Rt△BDC中,E为斜边BC的中点,
∴DE=BE.
在△OBE和△ODE中,
∴△OBE≌△ODE(SSS),
∴∠ODE=∠ABC=90°,即OD⊥DE.
又∵OD是半圆O的半径,
∴DE是半圆O的切线.
(2)在Rt△ABC中,∵∠BAC=30°,
∴BC=AC.
∵BC=2DE=4,∴AC=8.
又∵∠C=90°-∠BAC=60°,DE=BE=EC,
∴△DEC为等边三角形,∴DC=DE=2,
∴AD=AC-DC=6.
12.证明:如图图图,作直径DG,连接BG.
∵点E是△ABC的内心,
∴AD平分∠BAC,
∴∠BAD=∠DAC.
∵∠G=∠BAD,∠BDM=∠DAC,
∴∠BDM=∠G.
∵DG为⊙O的直径,∴∠GBD=90°,
∴∠G+∠BDG=90°,
∴∠BDM+∠BDG=90°,即∠MDG=90°.
又∵OD是⊙O的半径,
∴直线DM是⊙O的切线.
13.解:(1)证明:如图图图,过点O作OM⊥AB,垂足为M.
∵⊙O与AC相切于点D,∴OD⊥AC.
∵△ABC是等边三角形,∴AB=AC.
又∵AO⊥BC,
∴∠DAO=∠MAO.
又∵OM⊥AB,OD⊥AC,
∴OM=OD,∴AB与⊙O相切.
(2)如图图图,过点O作ON⊥BE,垂足为N,连接OF.
依题意得O是BC的中点,∴OB=2.
∵在Rt△OBM中,∠ABC=60°,OB=2,
∴BM=1,OM=.
∵BE⊥AB,OM⊥AB,ON⊥BE,
∴四边形OMBN是矩形,
∴ON=BM=1,BN=OM=.
在Rt△NOF中,∵OF=OM=,ON=1,
∴由勾股定理得NF=,
∴BF=BN+NF=+.
作法一 作半径或直径
①作半径(或直径):构造等腰三角形或直角三角形
1.如图图,△ABC是⊙O的内接三角形,∠C=30°,⊙O的半径为5.若P是⊙O上的一点,在△ABP中,PB=AB,则PA的长为( )
A.5 B. C.5 D.5
2.2019·绍兴如图图,△ABC内接于⊙O,∠B=65°,∠C=70°.若BC=2 ,则的长为( )
A.π B.π C.2π D.2 π
3.2020·攀枝花如图图,已知锐角三角形ABC内接于半径为2的⊙O,OD⊥BC于点D,∠BAC=60°,则OD=________.
②连接过切点的半径或直径:见切线,连切点,得垂直
4.2019·青岛如图图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为( )
A.π B.2π C.2 π D.4π
5.2019·台州如图图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为( )
A.2 B.3 C.4 D.4-
6.如图图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠A.
(1)求∠D的度数;
(2)若CD=2,求BD的长.
作法二 作弦心距:解决弦长的计算与证明问题
7.一条排水管的截面如图图所示,已知排水管的半径OA=1 m,水面宽AB=1.2 m,某天下雨后,排水管水面上升了0.2 m,则此时排水管水面宽为( )
A.1.4 m B.1.6 m C.1.8 m D.2 m
8.如图图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为2 ,则a的值是( )
A.2 B.2+ C.2 D.2+
作法三 构造直径所对的圆周角:见直径想直角
9.2020·泰安如图图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4 B.4 C. D.2
10.2019·绵阳如图图,AB是⊙O的直径,C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
作法四 判定直线与圆相切(作半径或作垂直)
①有交点 作半径,证垂直
11.如图图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆O交AC于点D,E为BC的中点,连接DE.
(1)求证:DE是半圆O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
12.如图图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.求证:直线DM是⊙O的切线.
②无交点 作垂直,证半径
13.如图图,△ABC是等边三角形,AO⊥BC,垂足为O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点.
(1)求证:AB与⊙O相切;
(2)若等边三角形ABC的边长是4,求线段BF的长.
答案
1.D 如图图图,连接OB,OA,
设OB与AP交于点D.由PB=AB可知=,从而可知OB⊥AP.运用“一条弧所对的圆周角等于它所对的圆心角的一半”及“同圆的半径相等”可知△OAB为等边三角形,在Rt△OAD中,运用“在直角三角形中,30°角所对的直角边等于斜边的一半”及勾股定理列方程可求得AD的长,从而可求出AP的长为5 .故选D.
2.A 在△ABC中,由三角形内角和定理,得∠A=180°-∠ABC-∠ACB=45°.
连接OB,OC,则∠BOC=2∠A=90°.
设圆的半径为r,由勾股定理,得r2+r2=(2 )2,解得r=2,所以的长为=π.
3.1 如图图图,连接OB,OC,
则易知∠BOC=2∠BAC=120°,由垂径定理可知∠BOD=∠BOC=60°,
则∠OBD=30°,∴OD=OB=1.
4.B 如图图图,连接CO,DO.
因为AC,BD分别与⊙O相切于点C,D,
所以∠ACO=∠BDO=90°.
又因为∠A=45°,
所以∠AOC=45°=∠A,所以CO=AC=4.
因为AC=BD,∠ACO=∠BDO,CO=DO,
所以△ACO≌△BDO,
所以∠DOB=∠AOC=45°,
所以∠DOC=180°-∠DOB-∠AOC=180°-45°-45°=90°,所以的长==2π.
故选B.
5.A 如图图图,设⊙O与AC的切点为E,连接AO,OE.
∵等边三角形ABC的边长为8,
∴AC=8,∠C=∠BAC=60°.
∵⊙O分别与边AB,AC相切,
∴∠OEC=90°,∠BAO=∠CAO=∠BAC=30°,
∴∠AOC=90°,
∴OC=AC=4.
在Rt△OCE中,∠OEC=90°,∠C=60°,
∴∠COE=30°,
∴CE=OC=2,∴OE=2 ,
∴⊙O的半径为2 .
6.解:(1)连接OC.
∵∠COD=2∠A,∠D=2∠A,
∴∠COD=∠D.
∵PD与⊙O相切于点C,
∴OC⊥PD,即∠OCD=90°,
∴∠D=×(180°-90°)=45°.
(2)由(1)可知∠COD=∠D,∴OC=CD=2.
由勾股定理,得OD==2 ,
∴BD=OD-OB=2 -2.
7.B 如图图图,过点O作OE⊥AB于点E,交CD于点F,连接OC.
∵AB=1.2 m,OE⊥AB,
∴AE=AB=0.6 m.
又∵OA=1 m,
∴由勾股定理,得OE=0.8 m.
∵排水管水面上升了0.2 m,
∴OF=0.8-0.2=0.6(m).
由题意可知CD∥AB.
∵OE⊥AB,∴OE⊥CD,
∴CF==0.8 m,CD=2CF,
∴CD=1.6 m.故选B.
8.B 如图图图,
连接PB,过点P作PC⊥AB于点C,过点P作横轴的垂线,垂足为E,交AB于点D,则PB=2,BC=.在Rt△PBC中,由勾股定理得PC=1.∵直线y=x平分第一象限的夹角,∴△PCD和△DEO都是等腰直角三角形,∴PD=,DE=OE=2,∴a=PE=2+.故选B.
9.B 连接CD,如图图图.
∵AB=BC,∠BAC=30°,
∴∠ACB=∠BAC=30°,
∴∠B=180°-30°-30°=120°,
∴∠D=180°-∠B=60°.
∵AD是直径,
∴∠ACD=90°,∴∠CAD=30°.
又∵AD=8,∴CD=AD=4,
∴AC===4 .
10.解:(1)证明:∵C为的中点,
∴=.
∵AB是⊙O的直径,且CF⊥AB,
∴=,∴=,
∴CD=BF.
在△BFG和△CDG中,
∴△BFG≌△CDG(AAS).
(2)解法一:如图图图①,连接OF.设⊙O的半径为r.
∵AB是⊙O的直径,
∴∠ADB=90°.
在Rt△ADB中,BD2=AB2-AD2,
即BD2=(2r)2-22.
在Rt△OEF中,OF2=OE2+EF2,
即EF2=r2-(r-2)2.
由(1)知==,
∴=,∴BD=CF,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2-22=4[r2-(r-2)2],
解得r=1(不合题意,舍去)或r=3,
∴BF2=EF2+BE2=32-(3-2)2+22=12,
∴BF=2 .
解法二:如图图图②,连接OC,交BD于点H.
∵C是的中点,
∴OC⊥BD,
∴DH=BH.
∵OA=OB,
∴OH=AD=1.
∵∠COE=∠BOH,∠OEC=∠OHB=90°,OC=OB,
∴△COE≌△BOH(AAS),
∴OE=OH=1,
∴OC=OB=OE+BE=3.
∵CF⊥AB,
∴CE=EF===2 ,
∴BF===2 .
11.解:(1)证明:如图图图,连接BD,OD,OE.
∵AB为半圆O的直径,
∴∠ADB=∠BDC=90°.
在Rt△BDC中,E为斜边BC的中点,
∴DE=BE.
在△OBE和△ODE中,
∴△OBE≌△ODE(SSS),
∴∠ODE=∠ABC=90°,即OD⊥DE.
又∵OD是半圆O的半径,
∴DE是半圆O的切线.
(2)在Rt△ABC中,∵∠BAC=30°,
∴BC=AC.
∵BC=2DE=4,∴AC=8.
又∵∠C=90°-∠BAC=60°,DE=BE=EC,
∴△DEC为等边三角形,∴DC=DE=2,
∴AD=AC-DC=6.
12.证明:如图图图,作直径DG,连接BG.
∵点E是△ABC的内心,
∴AD平分∠BAC,
∴∠BAD=∠DAC.
∵∠G=∠BAD,∠BDM=∠DAC,
∴∠BDM=∠G.
∵DG为⊙O的直径,∴∠GBD=90°,
∴∠G+∠BDG=90°,
∴∠BDM+∠BDG=90°,即∠MDG=90°.
又∵OD是⊙O的半径,
∴直线DM是⊙O的切线.
13.解:(1)证明:如图图图,过点O作OM⊥AB,垂足为M.
∵⊙O与AC相切于点D,∴OD⊥AC.
∵△ABC是等边三角形,∴AB=AC.
又∵AO⊥BC,
∴∠DAO=∠MAO.
又∵OM⊥AB,OD⊥AC,
∴OM=OD,∴AB与⊙O相切.
(2)如图图图,过点O作ON⊥BE,垂足为N,连接OF.
依题意得O是BC的中点,∴OB=2.
∵在Rt△OBM中,∠ABC=60°,OB=2,
∴BM=1,OM=.
∵BE⊥AB,OM⊥AB,ON⊥BE,
∴四边形OMBN是矩形,
∴ON=BM=1,BN=OM=.
在Rt△NOF中,∵OF=OM=,ON=1,
∴由勾股定理得NF=,
∴BF=BN+NF=+.
同课章节目录
