全国人教版数学九年级上册课课练:25.1.2概率(word版含答案)
文档属性
| 名称 | 全国人教版数学九年级上册课课练:25.1.2概率(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 555.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-30 21:38:37 | ||
图片预览


文档简介
[概率]
一、选择题
1.2020·温州一个不透明的布袋里装有7个只有颜色不同的球,其中4个白球,2个红球,1个黄球.从布袋里任意摸出1个球,是红球的概率为( )
A. B. C. D.
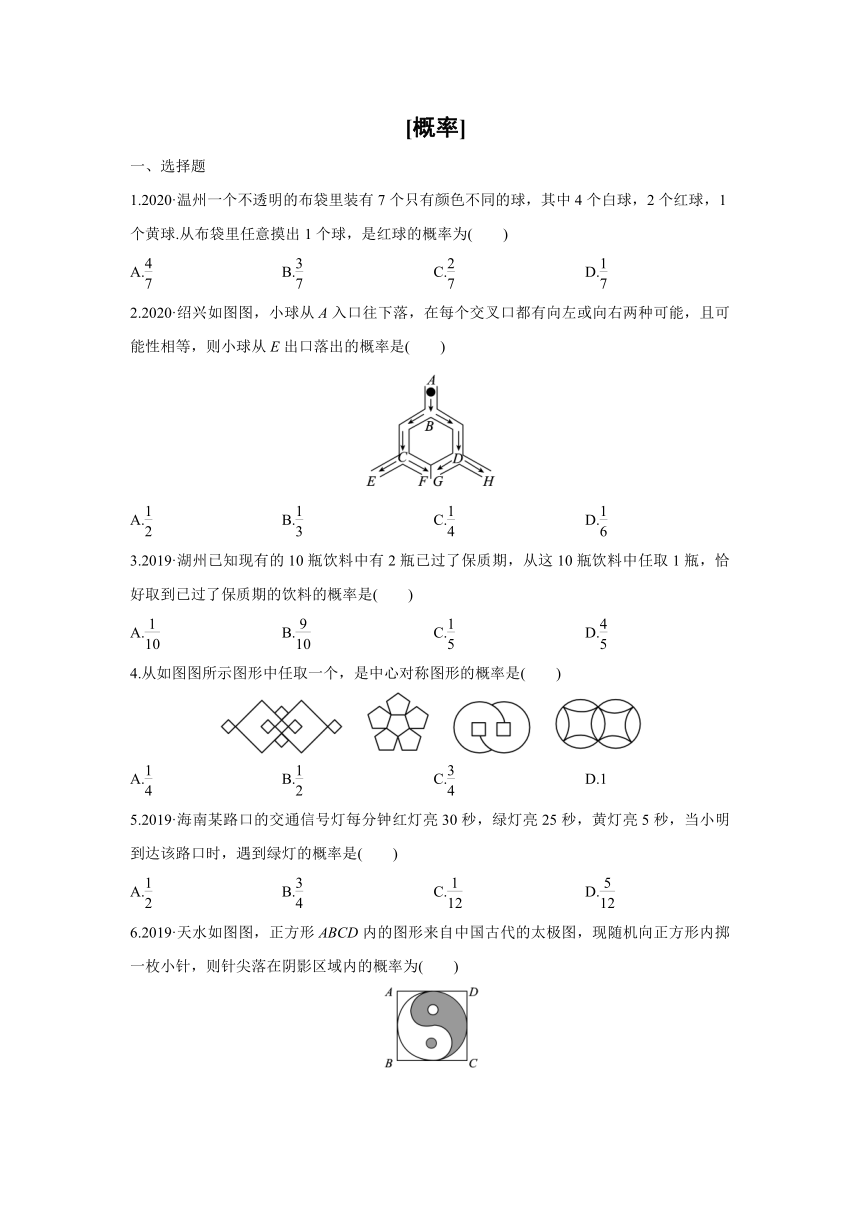
2.2020·绍兴如图图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等,则小球从E出口落出的概率是( )
A. B. C. D.
3.2019·湖州已知现有的10瓶饮料中有2瓶已过了保质期,从这10瓶饮料中任取1瓶,恰好取到已过了保质期的饮料的概率是( )
A. B. C. D.
4.从如图图所示图形中任取一个,是中心对称图形的概率是( )
A. B. C. D.1
5.2019·海南某路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小明到达该路口时,遇到绿灯的概率是( )
A. B. C. D.
6.2019·天水如图图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在阴影区域内的概率为( )
A. B. C. D.
7.如图图,在4×4的正方形网格中,阴影部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂上阴影,使阴影部分的图形仍然构成一个轴对称图形的概率是( )
A. B. C. D.
二、填空题
8.2019·岳阳分别写有数字,,-1,0,π的五张大小和质地均相同的卡片,从中任意抽取一张,抽到无理数的概率是________.
9.一枚质地均匀的骰子的6个面上分别刻有1~6的点数,抛掷这枚骰子一次,向上一面的点数是4的概率是________.
10.一只蚂蚁在如图图所示的树枝上寻觅食物,假定蚂蚁在岔路口随机选择一条路径,它获得食物的概率是________.
11.如图图,转盘中6个扇形的面积相等,任意转动转盘1次,转盘停止转动后,指针指向的数小于5的概率为________.
12.如图图所示的圆面图案是用半径相同的圆与圆弧构成的.若向圆面投掷飞镖,则飞镖落在阴影区域的概率为________.
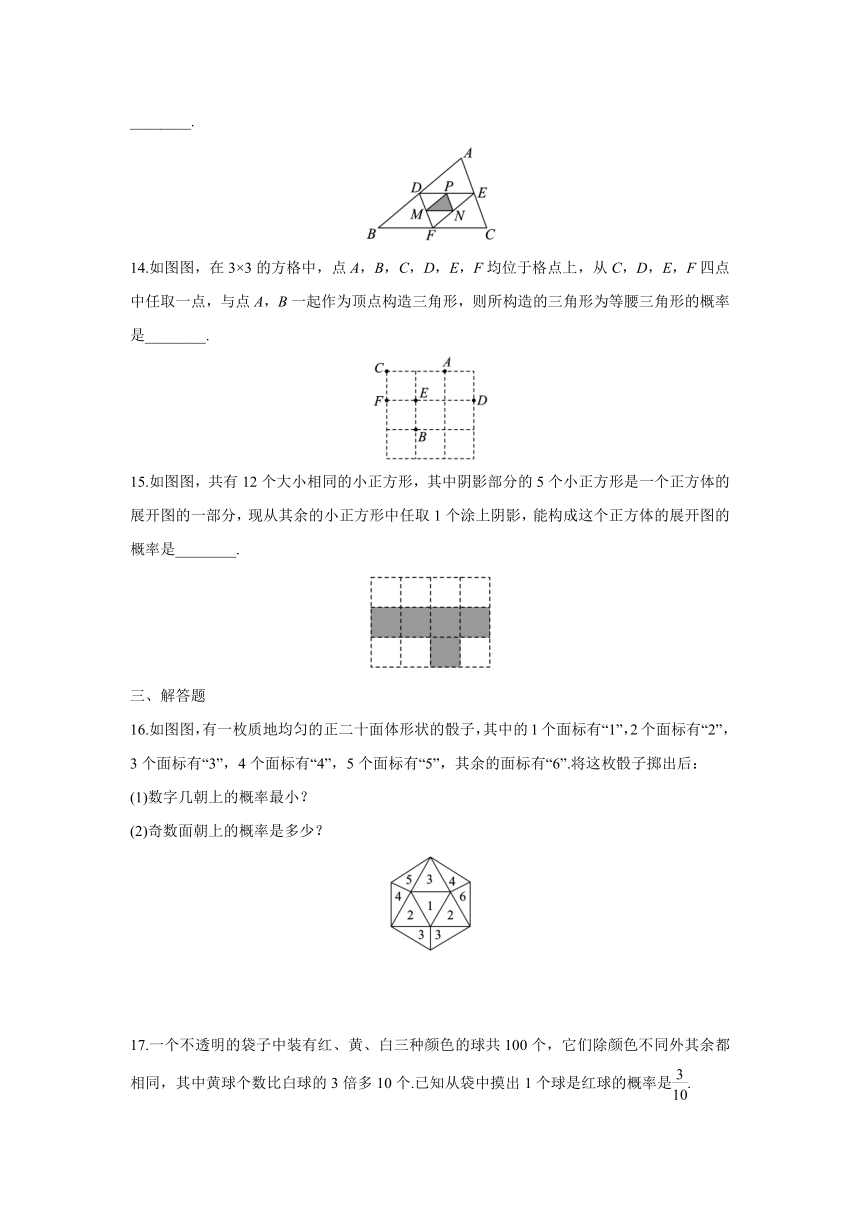
13.2020·随州如图图,在△ABC中,D,E,F分别为AB,AC,BC的中点,P,M,N分别为DE,DF,EF的中点,若随机向△ABC内投一粒米,则米粒落在图中阴影部分的概率为________.
14.如图图,在3×3的方格中,点A,B,C,D,E,F均位于格点上,从C,D,E,F四点中任取一点,与点A,B一起作为顶点构造三角形,则所构造的三角形为等腰三角形的概率是________.
15.如图图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的展开图的一部分,现从其余的小正方形中任取1个涂上阴影,能构成这个正方体的展开图的概率是________.
三、解答题
16.如图图,有一枚质地均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这枚骰子掷出后:
(1)数字几朝上的概率最小?
(2)奇数面朝上的概率是多少?
17.一个不透明的袋子中装有红、黄、白三种颜色的球共100个,它们除颜色不同外其余都相同,其中黄球个数比白球的3倍多10个.已知从袋中摸出1个球是红球的概率是.
(1)求袋中红球的个数;
(2)求从袋中摸出1个球是白球的概率;
(3)取走5个球(其中没有红球),求从剩余球中摸出1个球是红球的概率.
转化思想如图图①,在Rt△ABC中,∠C=90°,两条直角边长分别为a,b,斜边长为c.如图图图②,现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN.
(1)若Rt△ABC的两直角边长之比为2∶3,现随机向图②掷一枚小针,则针尖落在四个直角三角形区域的概率是多少?
(2)若正方形EFMN的边长为8,Rt△ABC的周长为18,求Rt△ABC的面积.
答案
1.C 2.C 3.C
4.C 因为共有4种等可能的结果,任取一个,是中心对称图形的有3种结果,所以任取一个,是中心对称图形的概率是.故选C.
5.D 一个循环是30+25+5=60(秒),所以遇到绿灯的概率为=.故选D.
6.C 设正方形ABCD的边长为2a,则针尖落在阴影区域内的概率==.
故选C.
7.B 因为根据轴对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合,白色的小正方形有13个,共13种情况,而能构成一个轴对称图形的有下列5种情况:
所以使阴影部分的图形仍然构成一个轴对称图形的概率是.故选B.
8. 五个数中和π是无理数,故从中任意抽取一张,抽到无理数的概率是.
9. 抛掷骰子一次,向上一面的点数可能是1,2,3,4,5,6,一共有6种等可能的结果,其中向上一面的点数是4的结果有1种,所以P(向上一面的点数是4)=.
10.
11. 转动转盘一次,出现6种等可能的结果,小于5的结果共有4种,故指针指向的数小于5的概率为=.
12.
13. ∵D,E,F分别为AB,AC,BC的中点,∴S△DEF=S△ABC.
∵P,M,N分别为DE,DF,EF的中点,
∴S△PMN=S△DEF,∴S△PMN=S△ABC,
∴米粒落在图中阴影部分的概率为.
14. 从C,D,E,F四点中任取一点,一共有4种等可能的结果.当选取点D,C,F时,所构造的三角形是等腰三角形,故P(所构造的三角形是等腰三角形)=.
15. 余下的小正方形共有7个,从上面的4个小正方形中任选一个涂上阴影都能构成正方体的展开图,所以任取1个小正方形涂上阴影,能构成正方体的展开图的概率为.
16.解:(1)因为骰子有20个面,1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”,
所以P(1朝上)=,P(2朝上)==,P(3朝上)=,P(4朝上)==,P(5朝上)==,P(6朝上)===,所以数字1朝上的概率最小.
(2)因为1—6中奇数有1,3,5,
所以P(奇数面朝上)==.
17.解:(1)根据题意,得100×=30(个).
答:袋中红球的个数是30个.
(2)设白球有x个,则黄球有(3x+10)个.
根据题意,得x+3x+10=100-30,
解得x=15,
则从袋中摸出1个球是白球的概率是=.
(3)因为取走5个球后,还剩95个球,且其中红球的个数没有变化,
所以从剩余球中摸出1个球是红球的概率是=.
[素养提升]
解:(1)因为Rt△ABC的两直角边长之比为2∶3,
所以设b=2k,a=3k,
由勾股定理,得c==k,
所以针尖落在四个直角三角形区域的概率为=.
(2)因为正方形EFMN的边长为8,所以c=8,所以a2+b2=c2=64.
因为Rt△ABC的周长为18,
即a+b+c=18,
所以a+b=10,
所以Rt△ABC的面积=ab
=[(a+b)2-(a2+b2)]
=9.
一、选择题
1.2020·温州一个不透明的布袋里装有7个只有颜色不同的球,其中4个白球,2个红球,1个黄球.从布袋里任意摸出1个球,是红球的概率为( )
A. B. C. D.
2.2020·绍兴如图图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等,则小球从E出口落出的概率是( )
A. B. C. D.
3.2019·湖州已知现有的10瓶饮料中有2瓶已过了保质期,从这10瓶饮料中任取1瓶,恰好取到已过了保质期的饮料的概率是( )
A. B. C. D.
4.从如图图所示图形中任取一个,是中心对称图形的概率是( )
A. B. C. D.1
5.2019·海南某路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小明到达该路口时,遇到绿灯的概率是( )
A. B. C. D.
6.2019·天水如图图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在阴影区域内的概率为( )
A. B. C. D.
7.如图图,在4×4的正方形网格中,阴影部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂上阴影,使阴影部分的图形仍然构成一个轴对称图形的概率是( )
A. B. C. D.
二、填空题
8.2019·岳阳分别写有数字,,-1,0,π的五张大小和质地均相同的卡片,从中任意抽取一张,抽到无理数的概率是________.
9.一枚质地均匀的骰子的6个面上分别刻有1~6的点数,抛掷这枚骰子一次,向上一面的点数是4的概率是________.
10.一只蚂蚁在如图图所示的树枝上寻觅食物,假定蚂蚁在岔路口随机选择一条路径,它获得食物的概率是________.
11.如图图,转盘中6个扇形的面积相等,任意转动转盘1次,转盘停止转动后,指针指向的数小于5的概率为________.
12.如图图所示的圆面图案是用半径相同的圆与圆弧构成的.若向圆面投掷飞镖,则飞镖落在阴影区域的概率为________.
13.2020·随州如图图,在△ABC中,D,E,F分别为AB,AC,BC的中点,P,M,N分别为DE,DF,EF的中点,若随机向△ABC内投一粒米,则米粒落在图中阴影部分的概率为________.
14.如图图,在3×3的方格中,点A,B,C,D,E,F均位于格点上,从C,D,E,F四点中任取一点,与点A,B一起作为顶点构造三角形,则所构造的三角形为等腰三角形的概率是________.
15.如图图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的展开图的一部分,现从其余的小正方形中任取1个涂上阴影,能构成这个正方体的展开图的概率是________.
三、解答题
16.如图图,有一枚质地均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这枚骰子掷出后:
(1)数字几朝上的概率最小?
(2)奇数面朝上的概率是多少?
17.一个不透明的袋子中装有红、黄、白三种颜色的球共100个,它们除颜色不同外其余都相同,其中黄球个数比白球的3倍多10个.已知从袋中摸出1个球是红球的概率是.
(1)求袋中红球的个数;
(2)求从袋中摸出1个球是白球的概率;
(3)取走5个球(其中没有红球),求从剩余球中摸出1个球是红球的概率.
转化思想如图图①,在Rt△ABC中,∠C=90°,两条直角边长分别为a,b,斜边长为c.如图图图②,现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN.
(1)若Rt△ABC的两直角边长之比为2∶3,现随机向图②掷一枚小针,则针尖落在四个直角三角形区域的概率是多少?
(2)若正方形EFMN的边长为8,Rt△ABC的周长为18,求Rt△ABC的面积.
答案
1.C 2.C 3.C
4.C 因为共有4种等可能的结果,任取一个,是中心对称图形的有3种结果,所以任取一个,是中心对称图形的概率是.故选C.
5.D 一个循环是30+25+5=60(秒),所以遇到绿灯的概率为=.故选D.
6.C 设正方形ABCD的边长为2a,则针尖落在阴影区域内的概率==.
故选C.
7.B 因为根据轴对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合,白色的小正方形有13个,共13种情况,而能构成一个轴对称图形的有下列5种情况:
所以使阴影部分的图形仍然构成一个轴对称图形的概率是.故选B.
8. 五个数中和π是无理数,故从中任意抽取一张,抽到无理数的概率是.
9. 抛掷骰子一次,向上一面的点数可能是1,2,3,4,5,6,一共有6种等可能的结果,其中向上一面的点数是4的结果有1种,所以P(向上一面的点数是4)=.
10.
11. 转动转盘一次,出现6种等可能的结果,小于5的结果共有4种,故指针指向的数小于5的概率为=.
12.
13. ∵D,E,F分别为AB,AC,BC的中点,∴S△DEF=S△ABC.
∵P,M,N分别为DE,DF,EF的中点,
∴S△PMN=S△DEF,∴S△PMN=S△ABC,
∴米粒落在图中阴影部分的概率为.
14. 从C,D,E,F四点中任取一点,一共有4种等可能的结果.当选取点D,C,F时,所构造的三角形是等腰三角形,故P(所构造的三角形是等腰三角形)=.
15. 余下的小正方形共有7个,从上面的4个小正方形中任选一个涂上阴影都能构成正方体的展开图,所以任取1个小正方形涂上阴影,能构成正方体的展开图的概率为.
16.解:(1)因为骰子有20个面,1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”,
所以P(1朝上)=,P(2朝上)==,P(3朝上)=,P(4朝上)==,P(5朝上)==,P(6朝上)===,所以数字1朝上的概率最小.
(2)因为1—6中奇数有1,3,5,
所以P(奇数面朝上)==.
17.解:(1)根据题意,得100×=30(个).
答:袋中红球的个数是30个.
(2)设白球有x个,则黄球有(3x+10)个.
根据题意,得x+3x+10=100-30,
解得x=15,
则从袋中摸出1个球是白球的概率是=.
(3)因为取走5个球后,还剩95个球,且其中红球的个数没有变化,
所以从剩余球中摸出1个球是红球的概率是=.
[素养提升]
解:(1)因为Rt△ABC的两直角边长之比为2∶3,
所以设b=2k,a=3k,
由勾股定理,得c==k,
所以针尖落在四个直角三角形区域的概率为=.
(2)因为正方形EFMN的边长为8,所以c=8,所以a2+b2=c2=64.
因为Rt△ABC的周长为18,
即a+b+c=18,
所以a+b=10,
所以Rt△ABC的面积=ab
=[(a+b)2-(a2+b2)]
=9.
同课章节目录
