全国人教版数学九年级上册课课练:25.3用频率估计概率(含答案解析)
文档属性
| 名称 | 全国人教版数学九年级上册课课练:25.3用频率估计概率(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 186.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-30 00:00:00 | ||
图片预览


文档简介
[用频率估计概率]
一、选择题
1.用频率估计概率可以发现,抛掷一枚均匀的硬币,“正面朝上”的概率为0.5,是指( )
A.连续抛掷2次,结果一定是“正面朝上”和“反面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.抛掷2n次,恰好有n次“正面朝上”
D.抛掷n次,当n越来越大时,“正面朝上”的频率会越来越接近0.5
2.2019·绍兴为了解某地区九年级男生的身高情况,随机抽取了该地区100名九年级男生,他们的身高x(cm)统计如图图下:
组别(cm) x<160 160≤x<170 170≤x<180 x≥180
人数 5 38 42 15
根据以上结果,抽查该地区一名九年级男生,估计他的身高不低于180 cm的概率是( )
A.0.85 B.0.57 C.0.42 D.0.15
3.如图图显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟此试验,则当投掷次数为1000时,“钉尖向上”的频率一定是0.620.
其中合理的是( )
A.① B.② C.①② D.①③
4.某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图如图图所示,则符合这一结果的试验可能是( )
A.抛掷一枚硬币,出现正面朝上
B.掷一枚正六面体骰子,向上一面的点数是3
C.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球、1个黑球的袋子中任取一个球,取到的是黑球
5.如图图,正方形ABCD内有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数为a,⊙O内的点数为b(在正方形边上和圆上的点不在统计中).根据用频率估计概率的原理,可推得π的大小是( )
A.π≈ B.π≈ C.π≈ D.π≈
二、填空题
6.2020·宜昌技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为________.(结果要求保留两位小数)
7.2020·广西某射击运动员在同一条件下的射击成绩记录如图图下:
射击次数 20 40 100 200 400 1000
“射中9环以 上”的次数 15 33 78 158 321 801
“射中9环以上”的频 率(结果保留小数点 后两位) 0.75 0.83 0.78 0.79 0.80 0.80
根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率是________(结果保留小数点后一位).
8.2020·马鞍山在一个不透明的袋子中装有6个红球和若干个白球,这些球除颜色外其余都相同,将球搅匀后随机摸出一个球,记下颜色后放回,不断重复这一过程,共摸球100次,发现有20次摸到红球,估计袋子中白球的个数约为________.
三、解答题
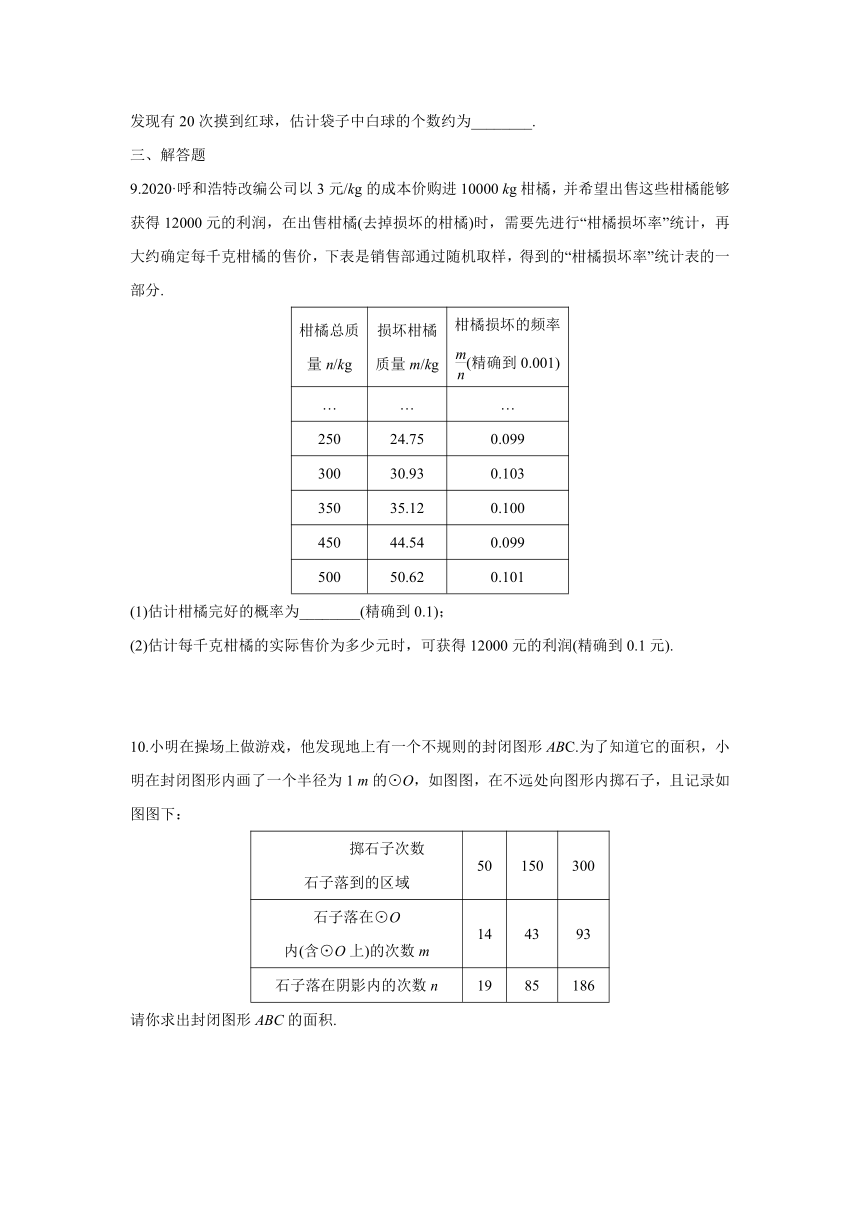
9.2020·呼和浩特改编公司以3元/kg的成本价购进10000 kg柑橘,并希望出售这些柑橘能够获得12000元的利润,在出售柑橘(去掉损坏的柑橘)时,需要先进行“柑橘损坏率”统计,再大约确定每千克柑橘的售价,下表是销售部通过随机取样,得到的“柑橘损坏率”统计表的一部分.
柑橘总质 量n/kg 损坏柑橘 质量m/kg 柑橘损坏的频率 (精确到0.001)
… … …
250 24.75 0.099
300 30.93 0.103
350 35.12 0.100
450 44.54 0.099
500 50.62 0.101
(1)估计柑橘完好的概率为________(精确到0.1);
(2)估计每千克柑橘的实际售价为多少元时,可获得12000元的利润(精确到0.1元).
10.小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,小明在封闭图形内画了一个半径为1 m的⊙O,如图图,在不远处向图形内掷石子,且记录如图图下:
掷石子次数 石子落到的区域 50 150 300
石子落在⊙O 内(含⊙O上)的次数m 14 43 93
石子落在阴影内的次数n 19 85 186
请你求出封闭图形ABC的面积.
统计思想一只不透明的袋子中装有4个小球,分别标有数字2,3,4,x,这些小球除所标数字不同外其余都相同.甲、乙两人每次同时从袋中各随机摸出1个小球,并计算摸出的这2个小球上的数字之和.记录后再将小球都放回袋中搅匀,进行重复试验.试验数据如图图下表:
摸球总次数 10 20 30 60 90 120 180 240 330 450
“和为7”出 现的次数 1 9 14 24 26 37 58 82 109 150
“和为7”出 现的频率 0.10 0.45 0.47 0.40 0.29 0.31 0.32 0.34 0.33 0.33
解答下列问题:
(1)如图图果试验继续进行下去,根据上表数据,试估计出现“和为7”的概率;
(2)根据(1),若x是不等于2,3,4的自然数,试求x的值.
答案
1.D
2.D 结合表格,根据频率=频数÷样本容量,即身高不低于180 cm的频率是15÷100=0.15,再用频率估计概率进行解答.
3.B
4.D 由折线图可知,这一结果出现的概率约为0.33.
A.抛掷一枚硬币,出现正面朝上的概率为=0.5,不符合题意;
B.掷一枚正六面体骰子,向上一面的点数是3的概率为≈0.17,不符合题意;
C.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为=0.25,不符合题意;
D.从一个装有2个红球、1个黑球的袋子中任取一个球,取到的是黑球的概率为≈0.33,符合题意.故选D.
5.B 设圆的半径为r,则正方形的边长为2r.根据题意,得≈,故π≈.故选B.
6.0.99
7.0.8 根据表格数据可知“射中9环以上”的频率稳定于0.8,所以估计这名运动员射击一次时“射中9环以上”的概率是0.8.
8.24 设白球有x个,根据题意,得=,解得x=24.
经检验,x=24是分式方程的解且符合题意,故白球的个数约为24个.
9.解:(1)0.9
(2)设每千克柑橘的实际销售价为x元,则应有10000×0.9x-3×10000=12000,
解得x=≈4.7.
答:每千克柑橘的实际售价约为4.7元时,可获得12000元的利润.
10.解:因为≈0.424,≈0.336,≈0.333,
所以P(石子落在⊙O内)≈.
又因为P(石子落在⊙O内)=,
所以≈,
所以S封闭图形ABC≈3S⊙O=3π m2.
[素养提升]
解:(1)估计出现“和为7”的概率是0.33.
(2)列表如图图下:
甲 和 乙 2 3 4 x
2 5 6 2+x
3 5 7 3+x
4 6 7 4+x
x 2+x 3+x 4+x
由表可知一共有12种等可能的结果.
由(1)可知,出现“和为7”的概率为0.33,
所以“和为7”出现的次数为0.33×12=3.96≈4.
若2+x=7,则x=5,此时P(“和为7”)=≈0.33,符合题意;
若3+x=7,则x=4,不符合题意;
若4+x=7,则x=3,不符合题意.
综上所述,x=5.
一、选择题
1.用频率估计概率可以发现,抛掷一枚均匀的硬币,“正面朝上”的概率为0.5,是指( )
A.连续抛掷2次,结果一定是“正面朝上”和“反面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.抛掷2n次,恰好有n次“正面朝上”
D.抛掷n次,当n越来越大时,“正面朝上”的频率会越来越接近0.5
2.2019·绍兴为了解某地区九年级男生的身高情况,随机抽取了该地区100名九年级男生,他们的身高x(cm)统计如图图下:
组别(cm) x<160 160≤x<170 170≤x<180 x≥180
人数 5 38 42 15
根据以上结果,抽查该地区一名九年级男生,估计他的身高不低于180 cm的概率是( )
A.0.85 B.0.57 C.0.42 D.0.15
3.如图图显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟此试验,则当投掷次数为1000时,“钉尖向上”的频率一定是0.620.
其中合理的是( )
A.① B.② C.①② D.①③
4.某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图如图图所示,则符合这一结果的试验可能是( )
A.抛掷一枚硬币,出现正面朝上
B.掷一枚正六面体骰子,向上一面的点数是3
C.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球、1个黑球的袋子中任取一个球,取到的是黑球
5.如图图,正方形ABCD内有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数为a,⊙O内的点数为b(在正方形边上和圆上的点不在统计中).根据用频率估计概率的原理,可推得π的大小是( )
A.π≈ B.π≈ C.π≈ D.π≈
二、填空题
6.2020·宜昌技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为________.(结果要求保留两位小数)
7.2020·广西某射击运动员在同一条件下的射击成绩记录如图图下:
射击次数 20 40 100 200 400 1000
“射中9环以 上”的次数 15 33 78 158 321 801
“射中9环以上”的频 率(结果保留小数点 后两位) 0.75 0.83 0.78 0.79 0.80 0.80
根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率是________(结果保留小数点后一位).
8.2020·马鞍山在一个不透明的袋子中装有6个红球和若干个白球,这些球除颜色外其余都相同,将球搅匀后随机摸出一个球,记下颜色后放回,不断重复这一过程,共摸球100次,发现有20次摸到红球,估计袋子中白球的个数约为________.
三、解答题
9.2020·呼和浩特改编公司以3元/kg的成本价购进10000 kg柑橘,并希望出售这些柑橘能够获得12000元的利润,在出售柑橘(去掉损坏的柑橘)时,需要先进行“柑橘损坏率”统计,再大约确定每千克柑橘的售价,下表是销售部通过随机取样,得到的“柑橘损坏率”统计表的一部分.
柑橘总质 量n/kg 损坏柑橘 质量m/kg 柑橘损坏的频率 (精确到0.001)
… … …
250 24.75 0.099
300 30.93 0.103
350 35.12 0.100
450 44.54 0.099
500 50.62 0.101
(1)估计柑橘完好的概率为________(精确到0.1);
(2)估计每千克柑橘的实际售价为多少元时,可获得12000元的利润(精确到0.1元).
10.小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,小明在封闭图形内画了一个半径为1 m的⊙O,如图图,在不远处向图形内掷石子,且记录如图图下:
掷石子次数 石子落到的区域 50 150 300
石子落在⊙O 内(含⊙O上)的次数m 14 43 93
石子落在阴影内的次数n 19 85 186
请你求出封闭图形ABC的面积.
统计思想一只不透明的袋子中装有4个小球,分别标有数字2,3,4,x,这些小球除所标数字不同外其余都相同.甲、乙两人每次同时从袋中各随机摸出1个小球,并计算摸出的这2个小球上的数字之和.记录后再将小球都放回袋中搅匀,进行重复试验.试验数据如图图下表:
摸球总次数 10 20 30 60 90 120 180 240 330 450
“和为7”出 现的次数 1 9 14 24 26 37 58 82 109 150
“和为7”出 现的频率 0.10 0.45 0.47 0.40 0.29 0.31 0.32 0.34 0.33 0.33
解答下列问题:
(1)如图图果试验继续进行下去,根据上表数据,试估计出现“和为7”的概率;
(2)根据(1),若x是不等于2,3,4的自然数,试求x的值.
答案
1.D
2.D 结合表格,根据频率=频数÷样本容量,即身高不低于180 cm的频率是15÷100=0.15,再用频率估计概率进行解答.
3.B
4.D 由折线图可知,这一结果出现的概率约为0.33.
A.抛掷一枚硬币,出现正面朝上的概率为=0.5,不符合题意;
B.掷一枚正六面体骰子,向上一面的点数是3的概率为≈0.17,不符合题意;
C.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为=0.25,不符合题意;
D.从一个装有2个红球、1个黑球的袋子中任取一个球,取到的是黑球的概率为≈0.33,符合题意.故选D.
5.B 设圆的半径为r,则正方形的边长为2r.根据题意,得≈,故π≈.故选B.
6.0.99
7.0.8 根据表格数据可知“射中9环以上”的频率稳定于0.8,所以估计这名运动员射击一次时“射中9环以上”的概率是0.8.
8.24 设白球有x个,根据题意,得=,解得x=24.
经检验,x=24是分式方程的解且符合题意,故白球的个数约为24个.
9.解:(1)0.9
(2)设每千克柑橘的实际销售价为x元,则应有10000×0.9x-3×10000=12000,
解得x=≈4.7.
答:每千克柑橘的实际售价约为4.7元时,可获得12000元的利润.
10.解:因为≈0.424,≈0.336,≈0.333,
所以P(石子落在⊙O内)≈.
又因为P(石子落在⊙O内)=,
所以≈,
所以S封闭图形ABC≈3S⊙O=3π m2.
[素养提升]
解:(1)估计出现“和为7”的概率是0.33.
(2)列表如图图下:
甲 和 乙 2 3 4 x
2 5 6 2+x
3 5 7 3+x
4 6 7 4+x
x 2+x 3+x 4+x
由表可知一共有12种等可能的结果.
由(1)可知,出现“和为7”的概率为0.33,
所以“和为7”出现的次数为0.33×12=3.96≈4.
若2+x=7,则x=5,此时P(“和为7”)=≈0.33,符合题意;
若3+x=7,则x=4,不符合题意;
若4+x=7,则x=3,不符合题意.
综上所述,x=5.
同课章节目录
