全国人教版数学九年级上册课课练:24章 圆 综合检测(word版含答案)
文档属性
| 名称 | 全国人教版数学九年级上册课课练:24章 圆 综合检测(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 767.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-30 21:21:12 | ||
图片预览

文档简介
第二十四章综合检测
[范围:圆 时间:90分钟 分值:100分]
一、选择题(本大题共10小题,每小题3分,共30分)
1.已知:如图图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( )
A.45° B.35° C.25° D.20°
2.已知⊙O的半径为5 cm,P是⊙O内一点,则OP的长可能是( )
A.4 cm B.5 cm C.6 cm D.7 cm
3.如图图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
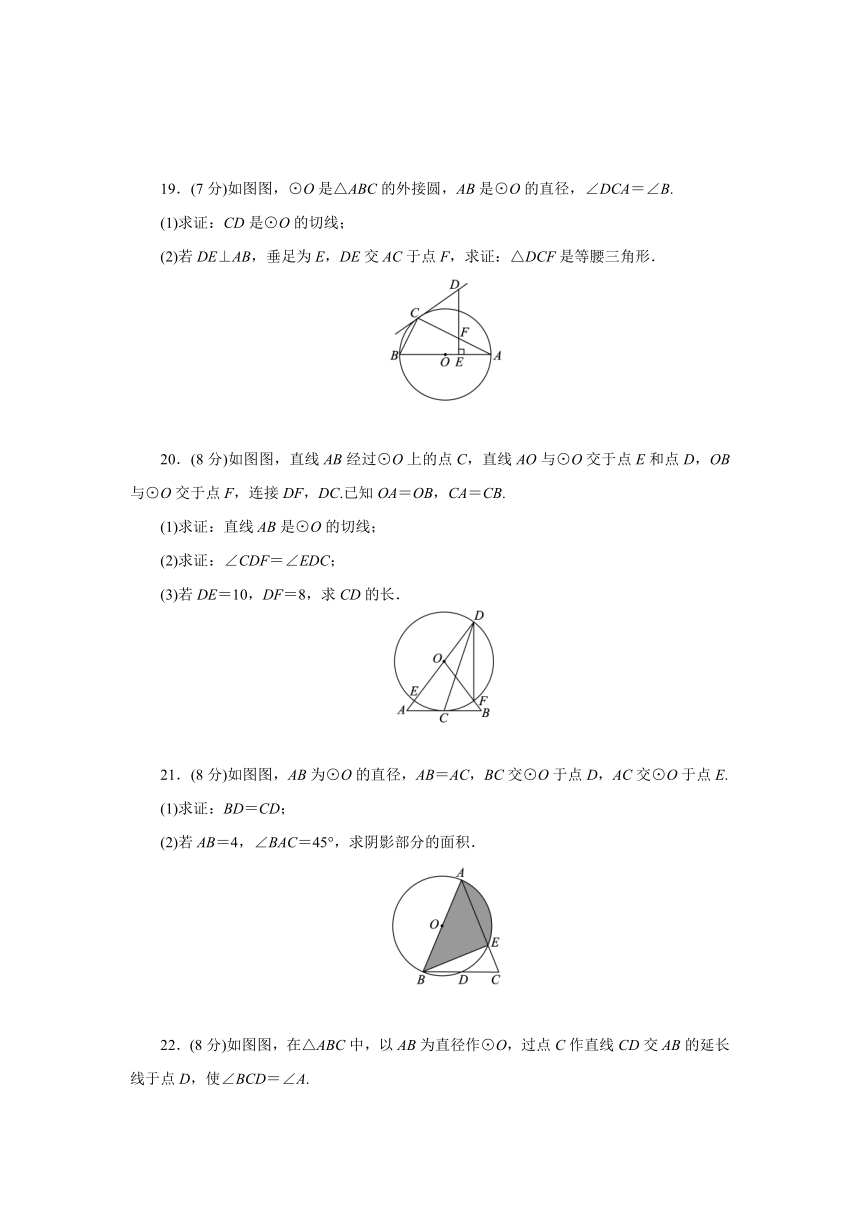
A.4 B.6.25 C.7.5 D.9
4.如图图,点A,B,C,D在⊙O上,∠AOC=120°,B是的中点,则∠D的度数是( )
A.30° B.40° C.50° D.60°
5.有一道题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A的度数.”嘉嘉的解答为:画△ABC以及它的外接圆⊙O,连接OB,OC,如图图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是( )
A.淇淇说得对,且∠A的另一个值是115°
B.淇淇说得不对,∠A就得65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同的值
6.如图图,AB为⊙O的切线,A为切点,OB交⊙O于点C,点D在⊙O上,连接AD,CD,OA,若∠ADC=35°,则∠ABO的度数为( )
A.25° B.20° C.30° D.35°
7.如图图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π B.3 π C.2 π D.2π
8.用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(如图图所示),则这个纸帽的高是( )
A. cm B.3 cm C.4 cm D.4 cm
9.如图图,A是⊙O上一点,BC是⊙O的直径,AC=2,AB=4,点D在⊙O上且平分,则CD的长为( )
A.2 B. C.2 D.
10.已知一个圆心角为270°的扇形工件,未搬动前如图图所示,A,B两点触地放置,搬动时,先将扇形以点B为圆心,作如图图图所示的无滑动旋转,再使它紧贴地面滚动,当A,B两点再次触地时停止,扇形工件所在圆的直径为6 m,则圆心O所经过的路线长是(结果用含π的式子表示)( )
A.6π m B.8π m C.10π m D.12π m
二、填空题(本大题共6小题,每小题3分,共18分)
11.一个圆内接正六边形的边长为2,那么这个正六边形的边心距为________.
12.如图图,C,D两点在以AB为直径的圆上,AB=2,∠ACD=30°,则AD=________.
13.当宽为3 cm的刻度尺的一边与⊙O相切于点A时,另一边与⊙O的两个交点B,C处的读数如图图所示(单位: cm),那么该圆的半径为________cm.
14.如图图(示意图),边长为2 cm的正六边形螺帽,中心为点O,OA垂直平分边CD,垂足为B,AB=17 cm,用扳手拧动螺帽旋转90°,则点A在该过程中所经过的路径长为________cm.
15.如图图,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,以AO长为半径画弧,分别与正方形的边相交,则图中阴影部分的面积为________.(结果保留π)
16.如图图所示,⊙O的半径是2,直线l与⊙O相交于A,B两点,M,N是⊙O上的两个动点,且在直线l的异侧.若∠AMB=45°,则四边形MANB面积的最大值是________.
三、解答题(本大题共7小题,共52分)
17.(6分)如图图,的半径OA=2,OC⊥AB于点C,∠AOC=60°.
(1)求弦AB的长;
(2)求的长.
18.(6分)如图图,在⊙O中,AB是⊙O的弦,CD是⊙O的直径,且AB⊥CD,垂足为G,点E在上,连接AE,CE,BE.
(1)求证:EC平分∠AEB;
(2)连接BC,若BC∥AE,且CG=4,AB=6,求BE的长.
19.(7分)如图图,⊙O是△ABC的外接圆,AB是⊙O的直径,∠DCA=∠B.
(1)求证:CD是⊙O的切线;
(2)若DE⊥AB,垂足为E,DE交AC于点F,求证:△DCF是等腰三角形.
20.(8分)如图图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF,DC.已知OA=OB,CA=CB.
(1)求证:直线AB是⊙O的切线;
(2)求证:∠CDF=∠EDC;
(3)若DE=10,DF=8,求CD的长.
21.(8分)如图图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.
(1)求证:BD=CD;
(2)若AB=4,∠BAC=45°,求阴影部分的面积.
22.(8分)如图图,在△ABC中,以AB为直径作⊙O,过点C作直线CD交AB的延长线于点D,使∠BCD=∠A.
(1)求证:CD为⊙O的切线;
(2)若DE平分∠ADC,且分别交AC,BC于点E,F,当CE=2时,求EF的长.
23.(9分)在△ABC中,AB=AC,O为AB上一动点,以点O为圆心,OB长为半径的圆交BC于点D,过点D作DE⊥AC,垂足为E.
(1)当O是AB的中点时,如图图①,判断DE与⊙O的位置关系.(直接写出结论,不必证明)
(2)当O不是AB的中点时,如图图图②,此时(1)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由.
(3)若⊙O与AC相切于点F,如图图图③,且⊙O的半径为3,CE=1,求AF的长.
答案
1.A 2.A 3.A
4.A 连接OB.∵B是的中点,
∴∠AOB=∠AOC=60°.
由圆周角定理,得∠D=∠AOB=30°.因此本题选A.
5.A 如图图图所示:
∠A还应有另一个不同的值,且∠A′与∠A互补,
故∠A′=180°-65°=115°.故选A.
6.B ∵AB与⊙O相切于点A,∴OA⊥AB,∴∠OAB=90°.∵∠AOC=2∠ADC,∠ADC=35°,∴∠AOC=70°,∴∠ABO=90°-70°=20°.因此本题选B.
7.A 如图图图,连接OB.
∵四边形OABC是平行四边形,
∴AB∥OC,AB=OC,∴AB=OA=OB,
∴△AOB是等边三角形,∴∠AOB=60°.
∵AB∥OC,∴S△AOB=S△ABC,
∴图中阴影部分的面积=S扇形OAB==6π.故选A.
8.C 设纸帽底面圆的半径为r cm,则2πr=,解得r=2.设圆锥的高为h cm,由勾股定理得h2+r2=62,所以h2+22=62,解得h=4 .
9.D ∵点D在⊙O上且平分,
∴=,
∴BD=CD.
∵BC是⊙O的直径,
∴∠BAC=∠D=90°.
∵AC=2,AB=4,
∴BC==2 .
在Rt△BDC中,由勾股定理,
得CD2+BD2=BC2,
∴2CD2=20,
∴CD=.
故选D.
10.A 如图图图,∠AOB=360°-270°=90°,则∠ABO=45°,
∴∠OBC=45°,
点O旋转的长度是2×=π(m),
点O移动的距离是=π(m),
则圆心O所经过的路线长是π+π=6π(m).
11.
12.1 ∵AB为⊙O的直径,
∴∠ADB=90°.
∵∠B=∠ACD=30°,
∴AD=AB=×2=1.
13.
14.10π 如图图图,连接OC,OD.
∵螺帽是正六边形,
∴△COD是等边三角形.
又∵OA垂直平分边CD,垂足为B,
∴CB=CD=×2 =,∴OB=3.
又∵AB=17,∴OA=AB+OB=17+3=20.
∵用扳手拧动螺帽旋转90°,∴点A在该过程中所经过的路径长为=10π(cm).
15.4-π 如图图图,因为正方形ABCD的边长为2,所以AO=AC=×=.
因为S正方形ABCD=22=4,S扇形EAF=,
所以S阴影部分=4-2×=4-π.
16.4
如图图图,
过点O作OC⊥AB于点C,交⊙O于D,E两点,连接OA,OB,DA,DB,EA,EB.
∵∠AMB=45°,
∴∠AOB=2∠AMB=90°.
又∵OA=OB,
∴△OAB为等腰直角三角形,
∴AB==2 .
∵S四边形MANB=S△MAB+S△NAB,
又当点M到AB的距离最大时,△MAB的面积最大;当点N到AB的距离最大时,△NAB的面积最大,
∴当点M运动到点D,点N运动到点E时,四边形MANB的面积最大,此时S四边形DAEB=S△DAB+S△EAB=AB·CD+AB·CE=AB·(CD+CE)=AB·DE=×2 ×4=4 .
17.解:(1)∵的半径OA=2,OC⊥AB于点C,∠AOC=60°,
∴∠OAC=30°,AC=BC=AB,
∴OC=1,则AC=,∴AB=2AC=2 .
(2)∵OA=OB,OC⊥AB,∠AOC=60°,
∴∠AOB=120°.
∵OA=2,∴的长是=.
18.解:(1)证明:∵CD⊥AB,CD是⊙O的直径,
∴=,
∴∠AEC=∠BEC,
∴EC平分∠AEB.
(2)∵CD⊥AB,
∴BG=AG=AB=3,∠BGC=90°.
在Rt△BGC中,
∵CG=4,BG=3,
∴BC=5.
∵BC∥AE,
∴∠AEC=∠BCE.
又∵∠AEC=∠BEC,
∴∠BCE=∠BEC,
∴BE=BC=5.
19.证明:(1)如图图图,连接OC.
∵OC=OA,
∴∠OCA=∠A.
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠A+∠B=90°.
又∵∠DCA=∠B,
∴∠OCA+∠DCA=∠OCD=90°,
∴OC⊥CD.
又∵点C在⊙O上,
∴CD是⊙O的切线.
(2)∵∠OCA+∠DCA=90°,∠OCA=∠A,
∴∠A+∠DCA=90°.
∵DE⊥AB,
∴∠A+∠EFA=90°,
∴∠DCA=∠EFA.
又∵∠EFA=∠DFC,
∴∠DCA=∠DFC,
∴DC=DF,∴△DCF是等腰三角形.
20.解:(1)证明:如图图图,连接OC.
∵OA=OB,CA=CB,
∴OC⊥AB.
又∵点C在⊙O上,
∴直线AB是⊙O的切线.
(2)证明:∵OA=OB,CA=CB,
∴∠AOC=∠BOC,
∴=,
∴∠CDF=∠EDC.
(3)如图图图,过点O作ON⊥DF于点N,延长DF交AB于点M.
∵ON⊥DF,
∴DN=NF=4.
在Rt△ODN中,∵∠OND=90°,OD=5,DN=4,
∴ON==3.
∵OC=OD,∴∠OCD=∠ODC.
又∵∠ODC=∠CDF,
∴∠OCD=∠CDF,
∴OC∥DF,
∴∠OCM+∠CMN=180°.
由(1)知∠OCM=90°,
∴∠CMN=90°=∠OCM=∠MNO,
∴四边形OCMN是矩形,
∴CM=ON=3,MN=OC=5.
在Rt△CDM中,∵∠DMC=90°,CM=3,DM=DN+MN=9,
∴CD===3.
21.解:(1)证明:如图图图,连接AD.
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC.
又∵AB=AC,
∴BD=CD.
(2)如图图图,连接OE.
∵AB=4,∠BAC=45°,
∴∠BOE=90°,BO=EO=2,∴∠AOE=90°,
∴S阴影=S△BOE+S扇形OAE=×2×2+=π+2.
22.解:(1)证明:如图图图,连接OC.
∵AB为⊙O的直径,
∴∠ACB=90°,∴∠A+∠ABC=90°.
∵OC=OB,
∴∠ABC=∠OCB.
又∵∠BCD=∠A,
∴∠BCD+∠OCB=90°,即∠OCD=90°.
又∵OC为⊙O的半径,
∴CD为⊙O的切线.
(2)∵DE平分∠ADC,∴∠CDE=∠ADE.
又∵∠BCD=∠A,
∴∠A+∠ADE=∠BCD+∠CDE,
即∠CEF=∠CFE,
∴CF=CE=2.
∵∠ACB=90°,
∴EF==2 .
23.解:(1)DE与⊙O相切.
(2)成立.
证明:连接OD.∵OB=OD,
∴∠B=∠ODB.
∵AB=AC,∴∠B=∠C,
∴∠ODB=∠C,∴OD∥AC.
∵DE⊥AC,
∴DE⊥OD.
又∵OD是⊙O的半径,
∴DE与⊙O相切,即(1)中的结论仍成立.
(3)连接OD,OF.由(2)知DE⊥OD,
∴∠ODE=90°.
∵AC与⊙O相切于点F,
∴∠OFE=90°.
∵DE⊥AC,
∴∠DEF=90°,
∴四边形ODEF是矩形.
又∵OD=OF,
∴四边形ODEF是正方形,
∴EF=OF=OB=3.
设AF=x,则AC=x+4,
∴AO=AB-OB=AC-OB=(x+4)-3=x+1.
在Rt△AOF中,
由勾股定理,得(x+1)2-x2=32,
解得x=4.∴AF=4.
[范围:圆 时间:90分钟 分值:100分]
一、选择题(本大题共10小题,每小题3分,共30分)
1.已知:如图图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( )
A.45° B.35° C.25° D.20°
2.已知⊙O的半径为5 cm,P是⊙O内一点,则OP的长可能是( )
A.4 cm B.5 cm C.6 cm D.7 cm
3.如图图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
A.4 B.6.25 C.7.5 D.9
4.如图图,点A,B,C,D在⊙O上,∠AOC=120°,B是的中点,则∠D的度数是( )
A.30° B.40° C.50° D.60°
5.有一道题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A的度数.”嘉嘉的解答为:画△ABC以及它的外接圆⊙O,连接OB,OC,如图图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是( )
A.淇淇说得对,且∠A的另一个值是115°
B.淇淇说得不对,∠A就得65°
C.嘉嘉求的结果不对,∠A应得50°
D.两人都不对,∠A应有3个不同的值
6.如图图,AB为⊙O的切线,A为切点,OB交⊙O于点C,点D在⊙O上,连接AD,CD,OA,若∠ADC=35°,则∠ABO的度数为( )
A.25° B.20° C.30° D.35°
7.如图图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π B.3 π C.2 π D.2π
8.用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(如图图所示),则这个纸帽的高是( )
A. cm B.3 cm C.4 cm D.4 cm
9.如图图,A是⊙O上一点,BC是⊙O的直径,AC=2,AB=4,点D在⊙O上且平分,则CD的长为( )
A.2 B. C.2 D.
10.已知一个圆心角为270°的扇形工件,未搬动前如图图所示,A,B两点触地放置,搬动时,先将扇形以点B为圆心,作如图图图所示的无滑动旋转,再使它紧贴地面滚动,当A,B两点再次触地时停止,扇形工件所在圆的直径为6 m,则圆心O所经过的路线长是(结果用含π的式子表示)( )
A.6π m B.8π m C.10π m D.12π m
二、填空题(本大题共6小题,每小题3分,共18分)
11.一个圆内接正六边形的边长为2,那么这个正六边形的边心距为________.
12.如图图,C,D两点在以AB为直径的圆上,AB=2,∠ACD=30°,则AD=________.
13.当宽为3 cm的刻度尺的一边与⊙O相切于点A时,另一边与⊙O的两个交点B,C处的读数如图图所示(单位: cm),那么该圆的半径为________cm.
14.如图图(示意图),边长为2 cm的正六边形螺帽,中心为点O,OA垂直平分边CD,垂足为B,AB=17 cm,用扳手拧动螺帽旋转90°,则点A在该过程中所经过的路径长为________cm.
15.如图图,在边长为2的正方形ABCD中,对角线AC的中点为O,分别以点A,C为圆心,以AO长为半径画弧,分别与正方形的边相交,则图中阴影部分的面积为________.(结果保留π)
16.如图图所示,⊙O的半径是2,直线l与⊙O相交于A,B两点,M,N是⊙O上的两个动点,且在直线l的异侧.若∠AMB=45°,则四边形MANB面积的最大值是________.
三、解答题(本大题共7小题,共52分)
17.(6分)如图图,的半径OA=2,OC⊥AB于点C,∠AOC=60°.
(1)求弦AB的长;
(2)求的长.
18.(6分)如图图,在⊙O中,AB是⊙O的弦,CD是⊙O的直径,且AB⊥CD,垂足为G,点E在上,连接AE,CE,BE.
(1)求证:EC平分∠AEB;
(2)连接BC,若BC∥AE,且CG=4,AB=6,求BE的长.
19.(7分)如图图,⊙O是△ABC的外接圆,AB是⊙O的直径,∠DCA=∠B.
(1)求证:CD是⊙O的切线;
(2)若DE⊥AB,垂足为E,DE交AC于点F,求证:△DCF是等腰三角形.
20.(8分)如图图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF,DC.已知OA=OB,CA=CB.
(1)求证:直线AB是⊙O的切线;
(2)求证:∠CDF=∠EDC;
(3)若DE=10,DF=8,求CD的长.
21.(8分)如图图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E.
(1)求证:BD=CD;
(2)若AB=4,∠BAC=45°,求阴影部分的面积.
22.(8分)如图图,在△ABC中,以AB为直径作⊙O,过点C作直线CD交AB的延长线于点D,使∠BCD=∠A.
(1)求证:CD为⊙O的切线;
(2)若DE平分∠ADC,且分别交AC,BC于点E,F,当CE=2时,求EF的长.
23.(9分)在△ABC中,AB=AC,O为AB上一动点,以点O为圆心,OB长为半径的圆交BC于点D,过点D作DE⊥AC,垂足为E.
(1)当O是AB的中点时,如图图①,判断DE与⊙O的位置关系.(直接写出结论,不必证明)
(2)当O不是AB的中点时,如图图图②,此时(1)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由.
(3)若⊙O与AC相切于点F,如图图图③,且⊙O的半径为3,CE=1,求AF的长.
答案
1.A 2.A 3.A
4.A 连接OB.∵B是的中点,
∴∠AOB=∠AOC=60°.
由圆周角定理,得∠D=∠AOB=30°.因此本题选A.
5.A 如图图图所示:
∠A还应有另一个不同的值,且∠A′与∠A互补,
故∠A′=180°-65°=115°.故选A.
6.B ∵AB与⊙O相切于点A,∴OA⊥AB,∴∠OAB=90°.∵∠AOC=2∠ADC,∠ADC=35°,∴∠AOC=70°,∴∠ABO=90°-70°=20°.因此本题选B.
7.A 如图图图,连接OB.
∵四边形OABC是平行四边形,
∴AB∥OC,AB=OC,∴AB=OA=OB,
∴△AOB是等边三角形,∴∠AOB=60°.
∵AB∥OC,∴S△AOB=S△ABC,
∴图中阴影部分的面积=S扇形OAB==6π.故选A.
8.C 设纸帽底面圆的半径为r cm,则2πr=,解得r=2.设圆锥的高为h cm,由勾股定理得h2+r2=62,所以h2+22=62,解得h=4 .
9.D ∵点D在⊙O上且平分,
∴=,
∴BD=CD.
∵BC是⊙O的直径,
∴∠BAC=∠D=90°.
∵AC=2,AB=4,
∴BC==2 .
在Rt△BDC中,由勾股定理,
得CD2+BD2=BC2,
∴2CD2=20,
∴CD=.
故选D.
10.A 如图图图,∠AOB=360°-270°=90°,则∠ABO=45°,
∴∠OBC=45°,
点O旋转的长度是2×=π(m),
点O移动的距离是=π(m),
则圆心O所经过的路线长是π+π=6π(m).
11.
12.1 ∵AB为⊙O的直径,
∴∠ADB=90°.
∵∠B=∠ACD=30°,
∴AD=AB=×2=1.
13.
14.10π 如图图图,连接OC,OD.
∵螺帽是正六边形,
∴△COD是等边三角形.
又∵OA垂直平分边CD,垂足为B,
∴CB=CD=×2 =,∴OB=3.
又∵AB=17,∴OA=AB+OB=17+3=20.
∵用扳手拧动螺帽旋转90°,∴点A在该过程中所经过的路径长为=10π(cm).
15.4-π 如图图图,因为正方形ABCD的边长为2,所以AO=AC=×=.
因为S正方形ABCD=22=4,S扇形EAF=,
所以S阴影部分=4-2×=4-π.
16.4
如图图图,
过点O作OC⊥AB于点C,交⊙O于D,E两点,连接OA,OB,DA,DB,EA,EB.
∵∠AMB=45°,
∴∠AOB=2∠AMB=90°.
又∵OA=OB,
∴△OAB为等腰直角三角形,
∴AB==2 .
∵S四边形MANB=S△MAB+S△NAB,
又当点M到AB的距离最大时,△MAB的面积最大;当点N到AB的距离最大时,△NAB的面积最大,
∴当点M运动到点D,点N运动到点E时,四边形MANB的面积最大,此时S四边形DAEB=S△DAB+S△EAB=AB·CD+AB·CE=AB·(CD+CE)=AB·DE=×2 ×4=4 .
17.解:(1)∵的半径OA=2,OC⊥AB于点C,∠AOC=60°,
∴∠OAC=30°,AC=BC=AB,
∴OC=1,则AC=,∴AB=2AC=2 .
(2)∵OA=OB,OC⊥AB,∠AOC=60°,
∴∠AOB=120°.
∵OA=2,∴的长是=.
18.解:(1)证明:∵CD⊥AB,CD是⊙O的直径,
∴=,
∴∠AEC=∠BEC,
∴EC平分∠AEB.
(2)∵CD⊥AB,
∴BG=AG=AB=3,∠BGC=90°.
在Rt△BGC中,
∵CG=4,BG=3,
∴BC=5.
∵BC∥AE,
∴∠AEC=∠BCE.
又∵∠AEC=∠BEC,
∴∠BCE=∠BEC,
∴BE=BC=5.
19.证明:(1)如图图图,连接OC.
∵OC=OA,
∴∠OCA=∠A.
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠A+∠B=90°.
又∵∠DCA=∠B,
∴∠OCA+∠DCA=∠OCD=90°,
∴OC⊥CD.
又∵点C在⊙O上,
∴CD是⊙O的切线.
(2)∵∠OCA+∠DCA=90°,∠OCA=∠A,
∴∠A+∠DCA=90°.
∵DE⊥AB,
∴∠A+∠EFA=90°,
∴∠DCA=∠EFA.
又∵∠EFA=∠DFC,
∴∠DCA=∠DFC,
∴DC=DF,∴△DCF是等腰三角形.
20.解:(1)证明:如图图图,连接OC.
∵OA=OB,CA=CB,
∴OC⊥AB.
又∵点C在⊙O上,
∴直线AB是⊙O的切线.
(2)证明:∵OA=OB,CA=CB,
∴∠AOC=∠BOC,
∴=,
∴∠CDF=∠EDC.
(3)如图图图,过点O作ON⊥DF于点N,延长DF交AB于点M.
∵ON⊥DF,
∴DN=NF=4.
在Rt△ODN中,∵∠OND=90°,OD=5,DN=4,
∴ON==3.
∵OC=OD,∴∠OCD=∠ODC.
又∵∠ODC=∠CDF,
∴∠OCD=∠CDF,
∴OC∥DF,
∴∠OCM+∠CMN=180°.
由(1)知∠OCM=90°,
∴∠CMN=90°=∠OCM=∠MNO,
∴四边形OCMN是矩形,
∴CM=ON=3,MN=OC=5.
在Rt△CDM中,∵∠DMC=90°,CM=3,DM=DN+MN=9,
∴CD===3.
21.解:(1)证明:如图图图,连接AD.
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC.
又∵AB=AC,
∴BD=CD.
(2)如图图图,连接OE.
∵AB=4,∠BAC=45°,
∴∠BOE=90°,BO=EO=2,∴∠AOE=90°,
∴S阴影=S△BOE+S扇形OAE=×2×2+=π+2.
22.解:(1)证明:如图图图,连接OC.
∵AB为⊙O的直径,
∴∠ACB=90°,∴∠A+∠ABC=90°.
∵OC=OB,
∴∠ABC=∠OCB.
又∵∠BCD=∠A,
∴∠BCD+∠OCB=90°,即∠OCD=90°.
又∵OC为⊙O的半径,
∴CD为⊙O的切线.
(2)∵DE平分∠ADC,∴∠CDE=∠ADE.
又∵∠BCD=∠A,
∴∠A+∠ADE=∠BCD+∠CDE,
即∠CEF=∠CFE,
∴CF=CE=2.
∵∠ACB=90°,
∴EF==2 .
23.解:(1)DE与⊙O相切.
(2)成立.
证明:连接OD.∵OB=OD,
∴∠B=∠ODB.
∵AB=AC,∴∠B=∠C,
∴∠ODB=∠C,∴OD∥AC.
∵DE⊥AC,
∴DE⊥OD.
又∵OD是⊙O的半径,
∴DE与⊙O相切,即(1)中的结论仍成立.
(3)连接OD,OF.由(2)知DE⊥OD,
∴∠ODE=90°.
∵AC与⊙O相切于点F,
∴∠OFE=90°.
∵DE⊥AC,
∴∠DEF=90°,
∴四边形ODEF是矩形.
又∵OD=OF,
∴四边形ODEF是正方形,
∴EF=OF=OB=3.
设AF=x,则AC=x+4,
∴AO=AB-OB=AC-OB=(x+4)-3=x+1.
在Rt△AOF中,
由勾股定理,得(x+1)2-x2=32,
解得x=4.∴AF=4.
同课章节目录
