2.1.3多项式 课件(共20页)
图片预览







文档简介
(共20张PPT)
人教版 七年级上
精品同步教学课件
第二章 整式的加减
2.1.3 多项式
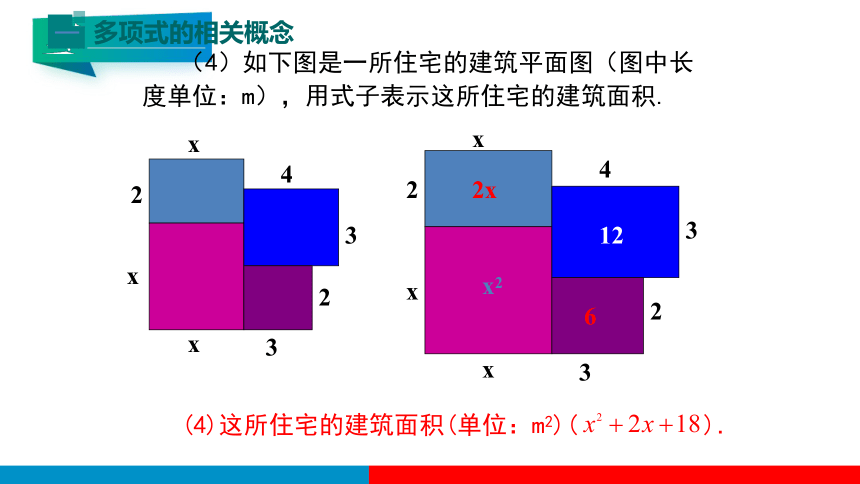
(4)这所住宅的建筑面积(单位:m2)( ).
(4)如下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
2
x
2x
x
x
x2
3
4
2
3
12
6
3
2
x
x
4
2
3
x
多项式的相关概念
一
3x+5y+2z
x2+2x+18
t-5
它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
议一议
上述几个式子都是两个或者多个单项式相加的形式.
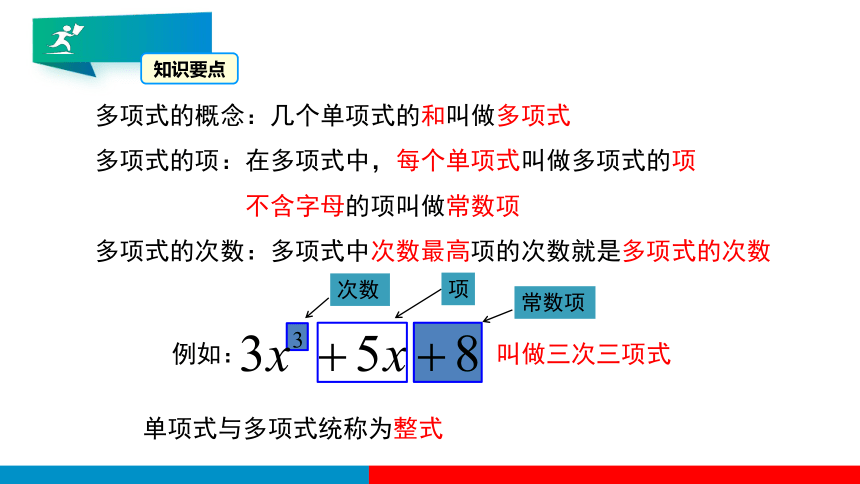
多项式的概念:几个单项式的和叫做多项式
多项式的项:在多项式中,每个单项式叫做多项式的项
不含字母的项叫做常数项
多项式的次数:多项式中次数最高项的次数就是多项式的次数
单项式与多项式统称为整式
例如:
常数项
次数
知识要点
项
叫做三次三项式
试一试
1.多项式x2+y-z是单项式___,___,___的和,
它是___次___项式.
2.多项式3m3-2m-5+m2的常数项是____,二次
项是_____,一次项的系数是_____.
x2
y
-z
二
三
-5
m2
﹣2
(1)多项式的各项应包括它前面的符号
(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的
(4)一个多项式的最高次项可以不唯一
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号
方法归纳
典例精析
例1 下列整式中哪些是多项式?是多项式的指出其项和次数:
解析
1
4
2
多项式a3b3-4ab4-b- 的最高次项是什么?一次项系数是什么?常数项是什么?它是几次几项式?
解:这个多项式的最高次项是a3b3,一次项系数是-1,常数项是- ,它是六次四项式.
练习
解题秘方:利用多项式的项及次数的定义进行辨析.
例2:已知-5xm+104xm+1-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,所以m=4.
归纳总结:解题的关键是弄清多项式次数是多项式中次数最高的项的次数.然后根据题意,列出方程,求出m的值.
分析:该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
所以该多项式为-5x4+104x5-4x4y2.
若关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,求m、n的值.
分析:多项式不含哪一项,则哪一项的系数为0.
解:由题意得m=0,n-1=0,所以n=1.
m,n当作已知常数看待,属于系数部分
针对训练
多项式的应用
二
例3 如图,用式子表示圆环的面积.当 cm,
cm 时,求圆环的面积( 取 ).
解:外圆的面积减去内圆的面积就是圆环
的面积,所以圆环的面积是 .
当 cm , cm 时,
圆环的面积(单位:cm2)是
做一做
一个花坛的形状如图所示,这的两端是半径相等的半圆,求:
(1)花坛的周长L;
(2)花坛的面积S.
解:(1) L=2a+2πr
(2) 花坛的面积是一个长方形的面积与两个半圆的面积 之和,即S=2ar+ πr2
a
r
r
当堂练习
1.下列式子中,哪些是单项式?哪些是多项式?哪些是整式?
3x,2x-1, ,-ab,-5, -1,3m-4n+m2n.
2.判断正误:
(1)多项式- x2y+2x2-y的次数2.( )
(2)多项式 -a+3a2的一次项系数是1.( )
(3)-x-y-z是三次三项式.( )
×
×
×
例 4
已知关于x 的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3 项和x2 项,求m,n 的值.
解题秘方:根据多项式的结构中不含某项的特征,结合相关定义,求出待定字母的值
解:因为关于x 的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3 项和x2 项,
所以-(m+5)=0,n-1=0,所以m=-5,n=1.
不含某一项,说明
这一项的系数为0
练习. 已知关于x 的多项式mx4-(5-m)x3+(2n+1)x2+3x3-3x+n不含x3 项和x2 项,试写出这个多项式,并求出当x=- 时, 多项式的值.
课堂小结
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数.
项:多式中的每个单项式叫多项式的项.
https://www.21cnjy.com/help/help_extract.php
人教版 七年级上
精品同步教学课件
第二章 整式的加减
2.1.3 多项式
(4)这所住宅的建筑面积(单位:m2)( ).
(4)如下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
2
x
2x
x
x
x2
3
4
2
3
12
6
3
2
x
x
4
2
3
x
多项式的相关概念
一
3x+5y+2z
x2+2x+18
t-5
它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
议一议
上述几个式子都是两个或者多个单项式相加的形式.
多项式的概念:几个单项式的和叫做多项式
多项式的项:在多项式中,每个单项式叫做多项式的项
不含字母的项叫做常数项
多项式的次数:多项式中次数最高项的次数就是多项式的次数
单项式与多项式统称为整式
例如:
常数项
次数
知识要点
项
叫做三次三项式
试一试
1.多项式x2+y-z是单项式___,___,___的和,
它是___次___项式.
2.多项式3m3-2m-5+m2的常数项是____,二次
项是_____,一次项的系数是_____.
x2
y
-z
二
三
-5
m2
﹣2
(1)多项式的各项应包括它前面的符号
(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的
(4)一个多项式的最高次项可以不唯一
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号
方法归纳
典例精析
例1 下列整式中哪些是多项式?是多项式的指出其项和次数:
解析
1
4
2
多项式a3b3-4ab4-b- 的最高次项是什么?一次项系数是什么?常数项是什么?它是几次几项式?
解:这个多项式的最高次项是a3b3,一次项系数是-1,常数项是- ,它是六次四项式.
练习
解题秘方:利用多项式的项及次数的定义进行辨析.
例2:已知-5xm+104xm+1-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,所以m=4.
归纳总结:解题的关键是弄清多项式次数是多项式中次数最高的项的次数.然后根据题意,列出方程,求出m的值.
分析:该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
所以该多项式为-5x4+104x5-4x4y2.
若关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,求m、n的值.
分析:多项式不含哪一项,则哪一项的系数为0.
解:由题意得m=0,n-1=0,所以n=1.
m,n当作已知常数看待,属于系数部分
针对训练
多项式的应用
二
例3 如图,用式子表示圆环的面积.当 cm,
cm 时,求圆环的面积( 取 ).
解:外圆的面积减去内圆的面积就是圆环
的面积,所以圆环的面积是 .
当 cm , cm 时,
圆环的面积(单位:cm2)是
做一做
一个花坛的形状如图所示,这的两端是半径相等的半圆,求:
(1)花坛的周长L;
(2)花坛的面积S.
解:(1) L=2a+2πr
(2) 花坛的面积是一个长方形的面积与两个半圆的面积 之和,即S=2ar+ πr2
a
r
r
当堂练习
1.下列式子中,哪些是单项式?哪些是多项式?哪些是整式?
3x,2x-1, ,-ab,-5, -1,3m-4n+m2n.
2.判断正误:
(1)多项式- x2y+2x2-y的次数2.( )
(2)多项式 -a+3a2的一次项系数是1.( )
(3)-x-y-z是三次三项式.( )
×
×
×
例 4
已知关于x 的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3 项和x2 项,求m,n 的值.
解题秘方:根据多项式的结构中不含某项的特征,结合相关定义,求出待定字母的值
解:因为关于x 的多项式3x4-(m+5)x3+(n-1)x2-5x+3不含x3 项和x2 项,
所以-(m+5)=0,n-1=0,所以m=-5,n=1.
不含某一项,说明
这一项的系数为0
练习. 已知关于x 的多项式mx4-(5-m)x3+(2n+1)x2+3x3-3x+n不含x3 项和x2 项,试写出这个多项式,并求出当x=- 时, 多项式的值.
课堂小结
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数.
项:多式中的每个单项式叫多项式的项.
https://www.21cnjy.com/help/help_extract.php
