人教版八年级上册11.2.1 三角形的内角和 课件 (共16张PPT)
文档属性
| 名称 | 人教版八年级上册11.2.1 三角形的内角和 课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-30 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
人教版数学八年级上册
第十一章 三角形
11.2 与三角形有关的角
11.2.1 三角形的内角和
1. 会用平行线的性质与平角的定义证明三角形内
角和等于180°;(重点)
2. 会运用三角形内角和定理进行计算.(难点)
教学目标
新课引入
问题1:回顾一下三角形的相关线段。
问题2:这节课我们开始学习三
角形的内角,你还记得三角形
的内角和是多少度吗?
测量难免有误差,可不可以用所学过的知识来证明三角形的内角和是180度呢?
问题3:当时,我们是如何验证它的呢?
探究新知1
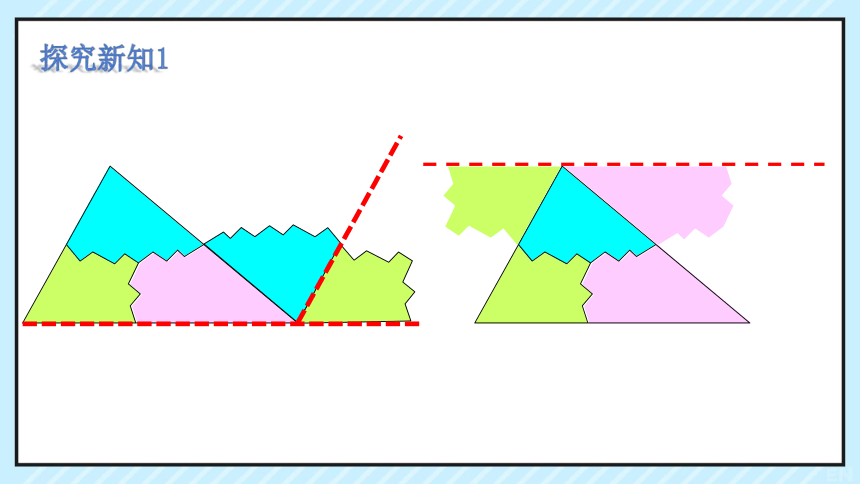
为了得到新思路,不妨先来剪一剪。
操作1:在纸上画一个三角形,再剪下来。
操作2:把三角形的三个内角剪下来,拼在一起。
探究新知1
问题4:在这个过程中,你发现我们验证的方法实质上利用了什么知识呢?
探究新知1
三角形的三个内角拼到
一起恰好构成一个平角,
平角为180度。
根据刚刚的两个图,你能想到什么方法来证明三角形的内角和为180度呢?
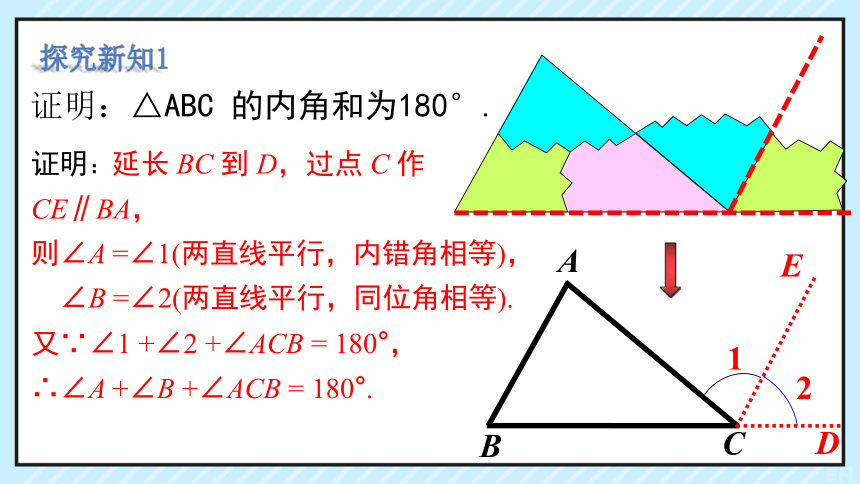
证明:△ABC 的内角和为180°.
探究新知1
证明:延长 BC 到 D,过点 C 作
CE∥BA,
则∠A =∠1(两直线平行,内错角相等),
∠B =∠2(两直线平行,同位角相等).
又∵∠1 +∠2 +∠ACB = 180°,
∴∠A +∠B +∠ACB = 180°.
C
B
A
E
D
1
2
证明:△ABC 的内角和为180°.
探究新知1
1
2
证明:过点 A 作 l∥BC,
则∠B =∠1,∠C =∠2
(两直线平行,内错角相等).
∵∠1 +∠2 +∠BAC = 180°,
∴∠B +∠C +∠BAC = 180°.
探究新知1
你还有其他的证明方法吗?
C
B
A
E
D
F
和同学们一起讨论一下,
并且写出你的证明过程。
巩固新知1
思考:在刚刚几张图里,有一些虚线,它们有什么作用?
帮助我们证明(做题)
在平面几何中,我们为了证明的需要,在原来的图形上添画的线叫做辅助线(虚线)。
同时,在这里我们运用了数学中的转化思想,将三角形的内角转化为一个平角。
巩固新知1
1.在△ABC中,∠A=35°,∠B=43 °,则∠C= .
2.在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是 三角形 .
3.在△ABC中,∠A=∠B+10°, ∠C=∠A+10°, 则∠A= ,∠ B= ,∠C= .
巩固新知1
4.如图,在△ABC中, ∠BAC= 36°,∠B = 80°,AD 是∠BAC的角平分线,求∠ADB 的度数.
A
B
C
D
巩固新知1
5.在△ABC 中, ∠A 的度数是∠B 的度数的 3 倍,∠C 比∠B 大 15°,求∠A,∠B,∠C 的度数.
巩固新知1
6.如图,在△ABC 中,∠A=∠B=∠ACB,CD 是 △ABC的高,CE 是∠ACB 的平分线,求∠DCE 的度数.
方程思想!
探究新知2:实际应用
如图,C 岛在 A 岛的北偏东 50°方向,B 岛在 A 岛的北偏东 80°方向,C 岛在 B 岛的北偏西 40°方向. 从 B 岛看 A,C 两岛的视角∠ABC 是多少度?从 C 岛看 A,B 两岛的视角∠ACB 呢?
北
A
D
北
C
B
东
E
巩固新知2:实际应用
如图,B 岛在 A 岛的南偏西 40° 方向,C 岛在 A 岛的南偏东 15°方向,C 岛在 B 岛的北偏东 80°方向,求从 C 岛看 A,B 两岛的视角∠ACB 的度数.
人教版数学八年级上册
第十一章 三角形
11.2 与三角形有关的角
11.2.1 三角形的内角和
1. 会用平行线的性质与平角的定义证明三角形内
角和等于180°;(重点)
2. 会运用三角形内角和定理进行计算.(难点)
教学目标
新课引入
问题1:回顾一下三角形的相关线段。
问题2:这节课我们开始学习三
角形的内角,你还记得三角形
的内角和是多少度吗?
测量难免有误差,可不可以用所学过的知识来证明三角形的内角和是180度呢?
问题3:当时,我们是如何验证它的呢?
探究新知1
为了得到新思路,不妨先来剪一剪。
操作1:在纸上画一个三角形,再剪下来。
操作2:把三角形的三个内角剪下来,拼在一起。
探究新知1
问题4:在这个过程中,你发现我们验证的方法实质上利用了什么知识呢?
探究新知1
三角形的三个内角拼到
一起恰好构成一个平角,
平角为180度。
根据刚刚的两个图,你能想到什么方法来证明三角形的内角和为180度呢?
证明:△ABC 的内角和为180°.
探究新知1
证明:延长 BC 到 D,过点 C 作
CE∥BA,
则∠A =∠1(两直线平行,内错角相等),
∠B =∠2(两直线平行,同位角相等).
又∵∠1 +∠2 +∠ACB = 180°,
∴∠A +∠B +∠ACB = 180°.
C
B
A
E
D
1
2
证明:△ABC 的内角和为180°.
探究新知1
1
2
证明:过点 A 作 l∥BC,
则∠B =∠1,∠C =∠2
(两直线平行,内错角相等).
∵∠1 +∠2 +∠BAC = 180°,
∴∠B +∠C +∠BAC = 180°.
探究新知1
你还有其他的证明方法吗?
C
B
A
E
D
F
和同学们一起讨论一下,
并且写出你的证明过程。
巩固新知1
思考:在刚刚几张图里,有一些虚线,它们有什么作用?
帮助我们证明(做题)
在平面几何中,我们为了证明的需要,在原来的图形上添画的线叫做辅助线(虚线)。
同时,在这里我们运用了数学中的转化思想,将三角形的内角转化为一个平角。
巩固新知1
1.在△ABC中,∠A=35°,∠B=43 °,则∠C= .
2.在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是 三角形 .
3.在△ABC中,∠A=∠B+10°, ∠C=∠A+10°, 则∠A= ,∠ B= ,∠C= .
巩固新知1
4.如图,在△ABC中, ∠BAC= 36°,∠B = 80°,AD 是∠BAC的角平分线,求∠ADB 的度数.
A
B
C
D
巩固新知1
5.在△ABC 中, ∠A 的度数是∠B 的度数的 3 倍,∠C 比∠B 大 15°,求∠A,∠B,∠C 的度数.
巩固新知1
6.如图,在△ABC 中,∠A=∠B=∠ACB,CD 是 △ABC的高,CE 是∠ACB 的平分线,求∠DCE 的度数.
方程思想!
探究新知2:实际应用
如图,C 岛在 A 岛的北偏东 50°方向,B 岛在 A 岛的北偏东 80°方向,C 岛在 B 岛的北偏西 40°方向. 从 B 岛看 A,C 两岛的视角∠ABC 是多少度?从 C 岛看 A,B 两岛的视角∠ACB 呢?
北
A
D
北
C
B
东
E
巩固新知2:实际应用
如图,B 岛在 A 岛的南偏西 40° 方向,C 岛在 A 岛的南偏东 15°方向,C 岛在 B 岛的北偏东 80°方向,求从 C 岛看 A,B 两岛的视角∠ACB 的度数.
