课件--从力做的功到向量的数量积[下学期]
文档属性
| 名称 | 课件--从力做的功到向量的数量积[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 651.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-08-30 00:00:00 | ||
图片预览


文档简介
课件16张PPT。
广东省江门市江海中学 董艳丽
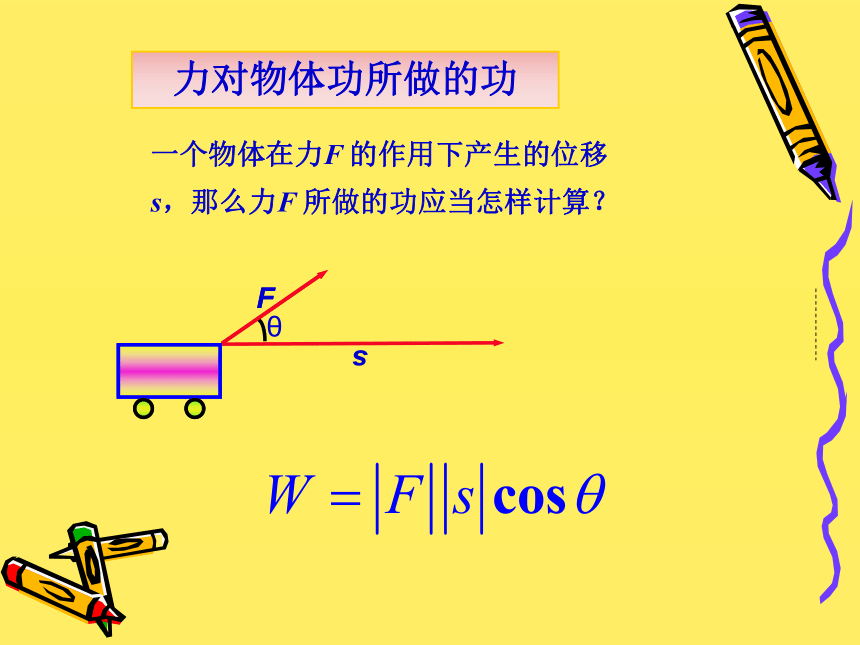
北师大版高中数学必修4第五节 从力做的功到向量的数量积力对物体功所做的功 一个物体在力F 的作用下产生的位移
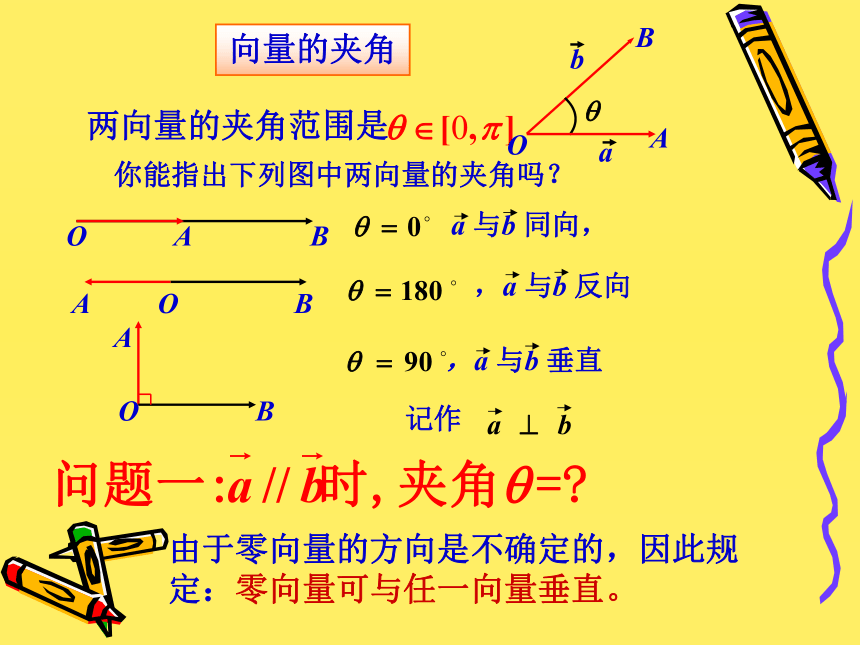
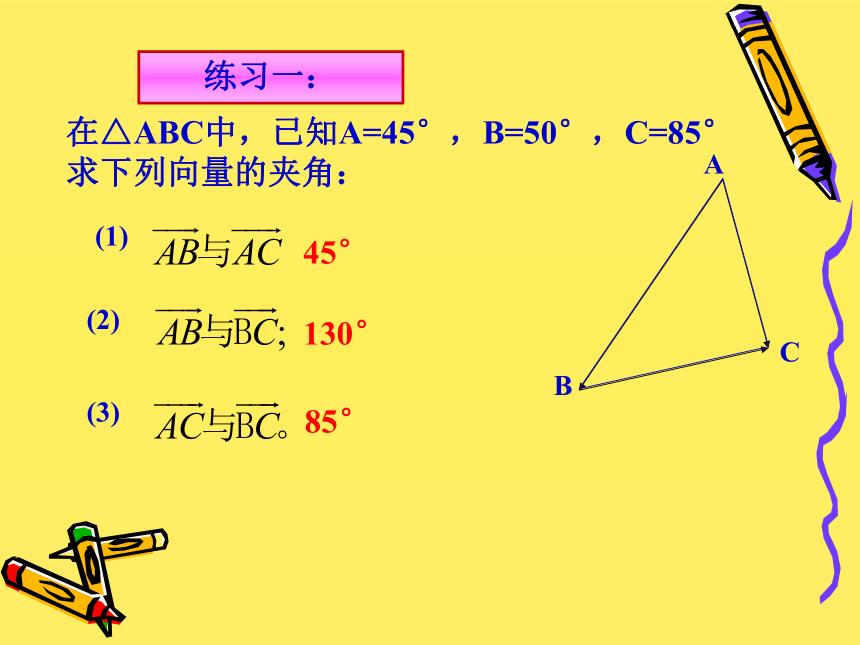
s,那么力F 所做的功应当怎样计算?向量的夹角你能指出下列图中两向量的夹角吗?由于零向量的方向是不确定的,因此规定:零向量可与任一向量垂直。练习一:在△ABC中,已知A=45°,B=50°,C=85°
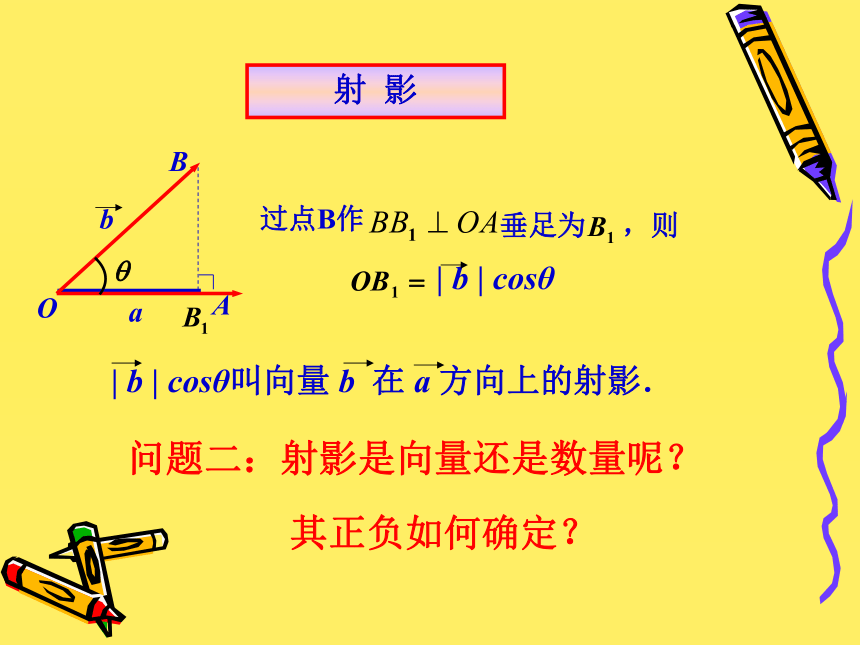
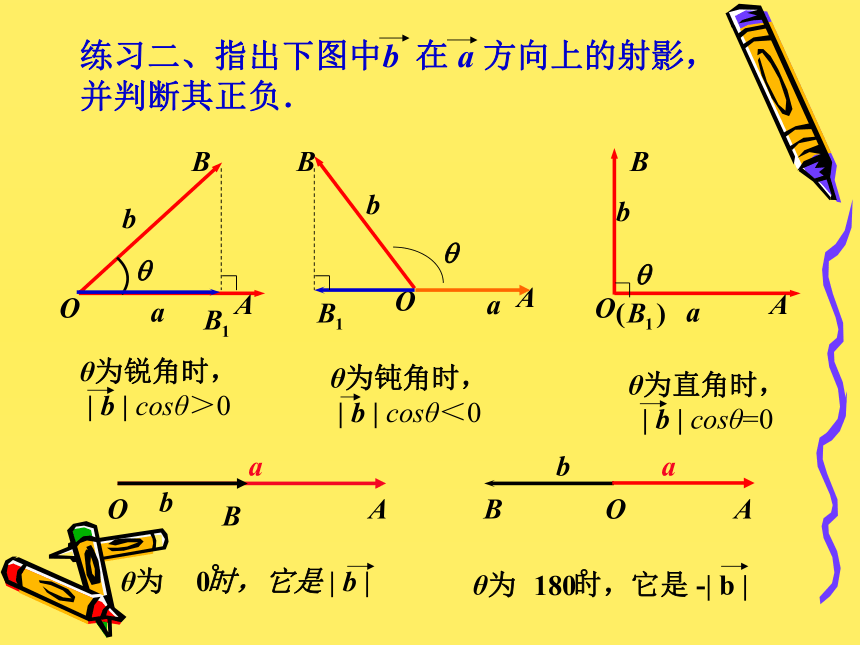
求下列向量的夹角: 45°130°85°射 影问题二:射影是向量还是数量呢?其正负如何确定?平面向量的数量积的定义 已知两个非零向量a 和b ,它们的夹角为? ,我们把数量
叫做a 与b 的数量积(或内积),记作a · b ,即规定:零向量与任意向量的数量积为0,即 注意: “ ”能不能写成“ ”或者“ ” 的形式。※向量数量积的物理意义是:力对物体做功。
就是力F与其作用下物体的位移s的数量积F·s向量数量积的意义0平面向量数量积的性质:演练反馈××√判断下列各题是否正确:(2)若 , ,则(3)若 , ,则(1)若 则对任一向量 ,有(4)√①平面向量的数量积及其性质;
②理解数量积的运算是不同于实数运算的一种新的运
算,注意它们的区别;
③主要题型有:求两向量的数量积、求向量的模、求两个
向量的夹角、判断两向量是否垂直及三角形的形状等。
下节课我们将进一步的学习。
④体会分类讨论、数形结合的思想。总结提炼作业:2、已知 1、 课本P108习题2-5,1(1) 3、4、5课后讨论 平面向量数量积,是两个向量之间的一种乘法运算,它与两个实数之间的乘法运算是否一样满足交换律、分配律、结合律呢?能否给出你的结论的证明?谢谢各位专家指导评定
广东省江门市江海中学 董艳丽
北师大版高中数学必修4第五节 从力做的功到向量的数量积力对物体功所做的功 一个物体在力F 的作用下产生的位移
s,那么力F 所做的功应当怎样计算?向量的夹角你能指出下列图中两向量的夹角吗?由于零向量的方向是不确定的,因此规定:零向量可与任一向量垂直。练习一:在△ABC中,已知A=45°,B=50°,C=85°
求下列向量的夹角: 45°130°85°射 影问题二:射影是向量还是数量呢?其正负如何确定?平面向量的数量积的定义 已知两个非零向量a 和b ,它们的夹角为? ,我们把数量
叫做a 与b 的数量积(或内积),记作a · b ,即规定:零向量与任意向量的数量积为0,即 注意: “ ”能不能写成“ ”或者“ ” 的形式。※向量数量积的物理意义是:力对物体做功。
就是力F与其作用下物体的位移s的数量积F·s向量数量积的意义0平面向量数量积的性质:演练反馈××√判断下列各题是否正确:(2)若 , ,则(3)若 , ,则(1)若 则对任一向量 ,有(4)√①平面向量的数量积及其性质;
②理解数量积的运算是不同于实数运算的一种新的运
算,注意它们的区别;
③主要题型有:求两向量的数量积、求向量的模、求两个
向量的夹角、判断两向量是否垂直及三角形的形状等。
下节课我们将进一步的学习。
④体会分类讨论、数形结合的思想。总结提炼作业:2、已知 1、 课本P108习题2-5,1(1) 3、4、5课后讨论 平面向量数量积,是两个向量之间的一种乘法运算,它与两个实数之间的乘法运算是否一样满足交换律、分配律、结合律呢?能否给出你的结论的证明?谢谢各位专家指导评定
