对数函数上课课件[上学期]
图片预览




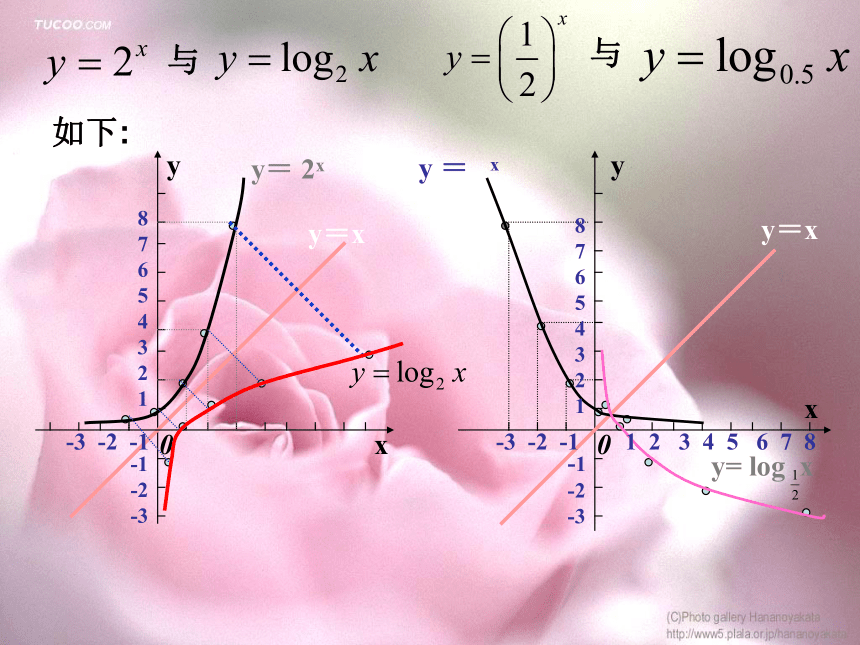

文档简介
课件17张PPT。对数函数深圳市西乡中学 曾广湘(一)1.问题情境:
在现实生活的细胞分裂过程中,细胞个数y 是分裂次数x 的指
只要知道了x 就能求出y 。数函数 现在反过来研究,知道了细胞个数, 如何确定分裂次数 ?为了求中的x 我们将写成对数式, 即从而得到一种新的函数一般地, 函数叫做对数函数,其定义域是下面做较详细的分析 对于指数函数 ,把它写成对数式为 ,这时 y 是自变量,x 是函数.
但习惯上用 x 表示自变量,y 表示函数,你知道这时函数
与函数 的图象有什么关系? (0, 1)(0, 1)(1, 0)学习了这节课后请同学们回答2.小组活动 采用描点法画出下列两组函数的图象.与由A组完成与由B组完成从所做出的图象上获取的信息, 与指数函数对比后你能获取哪些知识。与与如下:yx0y=xy= 2x8
7
6
5
4
3
2
1-3 -2 -1-1
-2
-3yxy=x0y = xy= log x8
7
6
5
4
3
2
11 2 3 4 5 6 7 8-3 -2 -1-1
-2
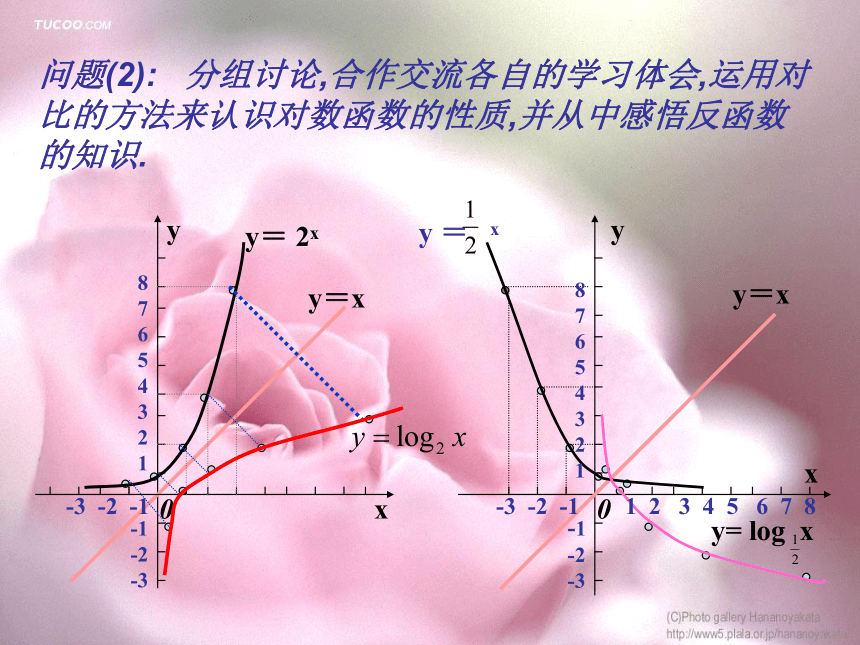
-33.问题探究你能根据下面的图象说些什么问题(1):观察已学过的指数函数图象, 运用自已的语言概括这些图形的共同特征。问题(2): 分组讨论,合作交流各自的学习体会,运用对比的方法来认识对数函数的性质,并从中感悟反函数的知识.yx0y=xy= 2x8
7
6
5
4
3
2
1-3 -2 -1-1
-2
-3yxy=x0y = xy= log x8
7
6
5
4
3
2
11 2 3 4 5 6 7 8-3 -2 -1-1
-2
-3问题(3): 对数函数性质( 0, + ∞ ) ( 0, + ∞ ) R R 增函数 减函数 (1,0) (1,0) 0 < x <1 时,y <0
x > 1 时,y > 0 0 < x <1 时,y > 0
x > 1 时,y < 0
思考底数 a 是如何影响函数 的。 问题(4)在同一坐标系中观察下列图象,你能从中获取什么信息.规律: 底大枝头低, 头低尾巴翘。(1).(2).(3).(4).(5).4.做一做例1:求下列函数的定义域
分析: (1) 要使真数有意义,则只要满足所以它的定义域是 (2) 要使这函数有意义,则只要满足所以它的定义域是变式引申
问题(1): 求的定义域问题(2): 求的定义域问题(3): 求的定义域用实物投影展示解题过程5. 数学应用利用对数函数的性质, 比较各组数中两个数的大小.与与分析: 这二题都是利用对数函数的单调性解题,不难
发现: 课外思考:问题(1):与问题(2):与掌握用“中间量”比较两个数的大小。谈一谈这一节课你的收获对数函数定义图象性质应用填写数学日记表 数学日记表回顾反思 本课的目的要求是掌握对数函数的概念、图象和性质.在理解对数函数的定义的基础上,掌握对数函数的图象和性质是本课的重点.作业:教材上习题2.7的第1题, 第2题, 第3题, 第6题, 第9题, 第11题.同学们再见!
在现实生活的细胞分裂过程中,细胞个数y 是分裂次数x 的指
只要知道了x 就能求出y 。数函数 现在反过来研究,知道了细胞个数, 如何确定分裂次数 ?为了求中的x 我们将写成对数式, 即从而得到一种新的函数一般地, 函数叫做对数函数,其定义域是下面做较详细的分析 对于指数函数 ,把它写成对数式为 ,这时 y 是自变量,x 是函数.
但习惯上用 x 表示自变量,y 表示函数,你知道这时函数
与函数 的图象有什么关系? (0, 1)(0, 1)(1, 0)学习了这节课后请同学们回答2.小组活动 采用描点法画出下列两组函数的图象.与由A组完成与由B组完成从所做出的图象上获取的信息, 与指数函数对比后你能获取哪些知识。与与如下:yx0y=xy= 2x8
7
6
5
4
3
2
1-3 -2 -1-1
-2
-3yxy=x0y = xy= log x8
7
6
5
4
3
2
11 2 3 4 5 6 7 8-3 -2 -1-1
-2
-33.问题探究你能根据下面的图象说些什么问题(1):观察已学过的指数函数图象, 运用自已的语言概括这些图形的共同特征。问题(2): 分组讨论,合作交流各自的学习体会,运用对比的方法来认识对数函数的性质,并从中感悟反函数的知识.yx0y=xy= 2x8
7
6
5
4
3
2
1-3 -2 -1-1
-2
-3yxy=x0y = xy= log x8
7
6
5
4
3
2
11 2 3 4 5 6 7 8-3 -2 -1-1
-2
-3问题(3): 对数函数性质( 0, + ∞ ) ( 0, + ∞ ) R R 增函数 减函数 (1,0) (1,0) 0 < x <1 时,y <0
x > 1 时,y > 0 0 < x <1 时,y > 0
x > 1 时,y < 0
思考底数 a 是如何影响函数 的。 问题(4)在同一坐标系中观察下列图象,你能从中获取什么信息.规律: 底大枝头低, 头低尾巴翘。(1).(2).(3).(4).(5).4.做一做例1:求下列函数的定义域
分析: (1) 要使真数有意义,则只要满足所以它的定义域是 (2) 要使这函数有意义,则只要满足所以它的定义域是变式引申
问题(1): 求的定义域问题(2): 求的定义域问题(3): 求的定义域用实物投影展示解题过程5. 数学应用利用对数函数的性质, 比较各组数中两个数的大小.与与分析: 这二题都是利用对数函数的单调性解题,不难
发现: 课外思考:问题(1):与问题(2):与掌握用“中间量”比较两个数的大小。谈一谈这一节课你的收获对数函数定义图象性质应用填写数学日记表 数学日记表回顾反思 本课的目的要求是掌握对数函数的概念、图象和性质.在理解对数函数的定义的基础上,掌握对数函数的图象和性质是本课的重点.作业:教材上习题2.7的第1题, 第2题, 第3题, 第6题, 第9题, 第11题.同学们再见!
