综合法证明不等式[上学期]
图片预览







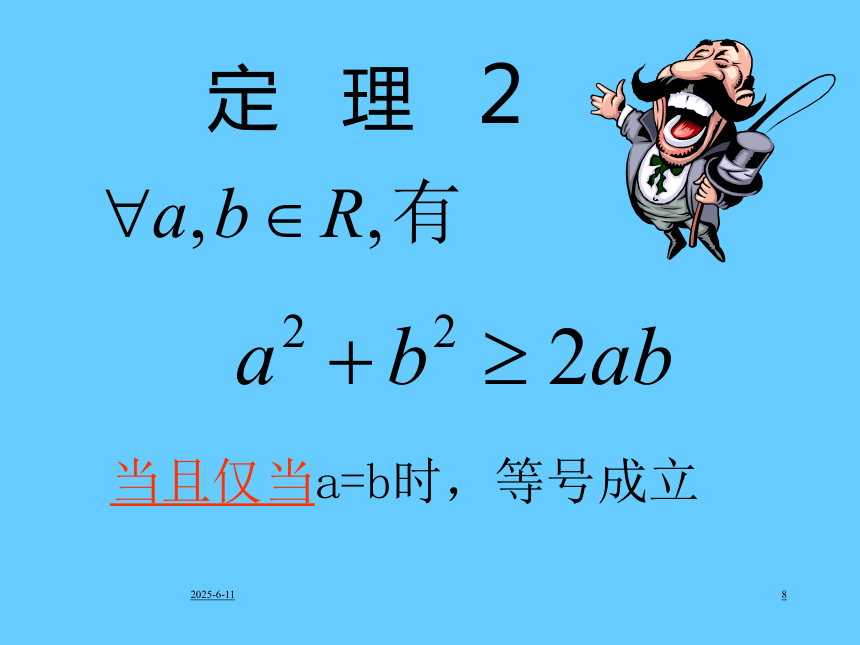

文档简介
课件26张PPT。2019/3/161不等式 欢迎你和它交朋友!2019/3/162教 学 方 法针对本节课需要学生严谨周密的逻辑思维的特点,整堂课实行引导,探索,综合 , 综合,归纳四步教学法。力求做到以创造发展为目的,以师生共同参与为核心,以反馈调控为手段,以推理判断为特征。
采用多媒体教学手段,增大教学容量和感官性。2019/3/163教 学 目 标知识目标: 综合法证明不等式
能力目标: 理解综合法证明不等式的意义。
熟练掌握过去学过的重要不等式,并用
这些不等式来证明新的不等式。
情感目标: 掌握综合法证明不等式,培养学生严谨
周密的逻辑思维习惯,加强学生实践能
力的训练,由因导果,进一步巩固学生
辩证唯物主义思想观念的教育,确实提
高学生的思想道德品质。
2019/3/164重 点、难 点重点:(1)掌握综合法证明不等式的基本思路,即“由因导果”。
(2)理解掌握用综合法证明不等式的逻辑关系。即A(已知)→B1→B2→‥‥→Bn→B(结论)
难点: “由因导果”时,从哪个不等式出发
合适是综合法证明不等式的难点!
2019/3/165回顾与反思例1例1 对于a,b∈R 求证:
证法一:2019/3/166思 考 可否用其他的方法证 仔细观察:左边是三项平方和形式,右边是两两乘积之和形式,我们可以联想到前面所学的定理2
( )
但项数不同,要动动脑筋,做一些适当的变形,例1 对于a,b∈R 求证:2019/3/167证法二由定理2知:对a,b,c∈R,有由不等式性质2的推论可知:
以上三个同向不等式可以相加再将以上不等式两边同时除以2,得:当且仅当a=b=c时,等号成立。2019/3/168定 理 2当且仅当a=b时,等号成立2019/3/169简 明 思 路
(三个同向不等式相加)当且仅当a=b=c时,等号成立2019/3/1610共 析“综合法”证明不等式实质上是“由因导果”的直接推理论证。其要点是:由已知性质定理出发,逐步导出其“必要条件”,直到最后的“必要条件”是所要证的不等式为止。2019/3/1611给你提个醒! 在利用综合法进行不等式证明时,要善于直接运用或创设条件运用基本不等式,其中拆项,并项,分解,组合是变形的重要技巧。
2019/3/1612 同学们,前面在1.3节我们学习了两个正数 的算术平均值与几何平均值的关系定理及其几个重要的不等式。这些都是在证明不等式过程中常用的关系:
证明不等式的常用关系当且仅当
a=b 时
等号成立2019/3/1613等 价 变 形可变形为 1)2)3)4)5)等等……2019/3/1614例5:若x,y,z是三个不尽相等的正实数,且 x+y+z=1 求证: (1-x)(1-y)(1-z)>8xy 怎么展开思路,寻找突破口?1 可是关键哟!2019/3/1615例题5 证 明 : 由已知条件x+y+z=1 及定理4可以知
1-z=x+y≥2
1-y=x+z≥2
1-x=y+z≥2但由于x,y,z不尽相等,就是说其中至少有两个数不相
等,故以上三个不等式至少有一个不等式是严格不等
式(不含等号)所以以上三个同向不等式相乘就得出:
(1-x)(1-y)(1-z)>即 (1-x)(1-y)(1-z)>8xyz2019/3/1616即定理42019/3/1617随堂练习1)若a,b∈R+ 则
2) 若a,b∈R+ 则 (a+b)(a2+b2)(a3+b3) ≥ 8a3b3
3) 若 a,b ∈R+ 且a≠b 则(a+b)(a3+b3) > (a2+b2)2
4) 若a,b ∈R 则 a2+b2+c2 +3≥ 2(a+b+c)2019/3/1618题 1 简 明 思 路2019/3/1619题 2 简 明 思 路若a,b∈R+ 则 (a+b)(a2+b2)(a3+b3) ≥ 8a3b3(a+b)(a2+b2)(a3+b3) ≥ 8a3b32019/3/1620题 3 简 明 思 路若 a,b ∈R+ 且a≠b 则(a+b)(a3+b3) > (a2+b2)2?2019/3/1621题 4 简 明 思 路若a,b ∈R 则 a2+b2+c2 +3≥ 2(a+b+c)2019/3/1622课 时 小 结 本节课我们学习了“综合法”证明不等式。其核心是引导我们运用已有知识(已知或已证成立的不等式或定理)进行逻辑思考和推理论证,启发我们大家从不同角度去
思考问题,去主动获取新知识。
教材中主要讲授了运用均值不等式来证明不等式,因而要加强对这个定理及它的各种各样的变形形式的理解。2019/3/1623 布 置 作 业 一,习题2—3 (课本P86)第5,6,7,8题
二,思考题:设a,b,c为一个不等边三角形的三边
边长,求证:
abc > (b+c-a)(a+b-c)(c+a-b)
(轮换不等式展现数学的另一种美)
三,1.预习新课“分析法”证明不等式
2.预习提纲
1)什么是分析法证明不等式?它的基本思
想是什么?
2)分析法适合证明哪类不等式?2019/3/1624板书设计 综合法证明不等式概念
应用
[例题3]
[例题4]
课堂练习
课时小结
课后作业2019/3/1625敬请多多指教星子实验中学
周 荣2019/3/1626敬请多多指教星子实验中学 周 荣
采用多媒体教学手段,增大教学容量和感官性。2019/3/163教 学 目 标知识目标: 综合法证明不等式
能力目标: 理解综合法证明不等式的意义。
熟练掌握过去学过的重要不等式,并用
这些不等式来证明新的不等式。
情感目标: 掌握综合法证明不等式,培养学生严谨
周密的逻辑思维习惯,加强学生实践能
力的训练,由因导果,进一步巩固学生
辩证唯物主义思想观念的教育,确实提
高学生的思想道德品质。
2019/3/164重 点、难 点重点:(1)掌握综合法证明不等式的基本思路,即“由因导果”。
(2)理解掌握用综合法证明不等式的逻辑关系。即A(已知)→B1→B2→‥‥→Bn→B(结论)
难点: “由因导果”时,从哪个不等式出发
合适是综合法证明不等式的难点!
2019/3/165回顾与反思例1例1 对于a,b∈R 求证:
证法一:2019/3/166思 考 可否用其他的方法证 仔细观察:左边是三项平方和形式,右边是两两乘积之和形式,我们可以联想到前面所学的定理2
( )
但项数不同,要动动脑筋,做一些适当的变形,例1 对于a,b∈R 求证:2019/3/167证法二由定理2知:对a,b,c∈R,有由不等式性质2的推论可知:
以上三个同向不等式可以相加再将以上不等式两边同时除以2,得:当且仅当a=b=c时,等号成立。2019/3/168定 理 2当且仅当a=b时,等号成立2019/3/169简 明 思 路
(三个同向不等式相加)当且仅当a=b=c时,等号成立2019/3/1610共 析“综合法”证明不等式实质上是“由因导果”的直接推理论证。其要点是:由已知性质定理出发,逐步导出其“必要条件”,直到最后的“必要条件”是所要证的不等式为止。2019/3/1611给你提个醒! 在利用综合法进行不等式证明时,要善于直接运用或创设条件运用基本不等式,其中拆项,并项,分解,组合是变形的重要技巧。
2019/3/1612 同学们,前面在1.3节我们学习了两个正数 的算术平均值与几何平均值的关系定理及其几个重要的不等式。这些都是在证明不等式过程中常用的关系:
证明不等式的常用关系当且仅当
a=b 时
等号成立2019/3/1613等 价 变 形可变形为 1)2)3)4)5)等等……2019/3/1614例5:若x,y,z是三个不尽相等的正实数,且 x+y+z=1 求证: (1-x)(1-y)(1-z)>8xy 怎么展开思路,寻找突破口?1 可是关键哟!2019/3/1615例题5 证 明 : 由已知条件x+y+z=1 及定理4可以知
1-z=x+y≥2
1-y=x+z≥2
1-x=y+z≥2但由于x,y,z不尽相等,就是说其中至少有两个数不相
等,故以上三个不等式至少有一个不等式是严格不等
式(不含等号)所以以上三个同向不等式相乘就得出:
(1-x)(1-y)(1-z)>即 (1-x)(1-y)(1-z)>8xyz2019/3/1616即定理42019/3/1617随堂练习1)若a,b∈R+ 则
2) 若a,b∈R+ 则 (a+b)(a2+b2)(a3+b3) ≥ 8a3b3
3) 若 a,b ∈R+ 且a≠b 则(a+b)(a3+b3) > (a2+b2)2
4) 若a,b ∈R 则 a2+b2+c2 +3≥ 2(a+b+c)2019/3/1618题 1 简 明 思 路2019/3/1619题 2 简 明 思 路若a,b∈R+ 则 (a+b)(a2+b2)(a3+b3) ≥ 8a3b3(a+b)(a2+b2)(a3+b3) ≥ 8a3b32019/3/1620题 3 简 明 思 路若 a,b ∈R+ 且a≠b 则(a+b)(a3+b3) > (a2+b2)2?2019/3/1621题 4 简 明 思 路若a,b ∈R 则 a2+b2+c2 +3≥ 2(a+b+c)2019/3/1622课 时 小 结 本节课我们学习了“综合法”证明不等式。其核心是引导我们运用已有知识(已知或已证成立的不等式或定理)进行逻辑思考和推理论证,启发我们大家从不同角度去
思考问题,去主动获取新知识。
教材中主要讲授了运用均值不等式来证明不等式,因而要加强对这个定理及它的各种各样的变形形式的理解。2019/3/1623 布 置 作 业 一,习题2—3 (课本P86)第5,6,7,8题
二,思考题:设a,b,c为一个不等边三角形的三边
边长,求证:
abc > (b+c-a)(a+b-c)(c+a-b)
(轮换不等式展现数学的另一种美)
三,1.预习新课“分析法”证明不等式
2.预习提纲
1)什么是分析法证明不等式?它的基本思
想是什么?
2)分析法适合证明哪类不等式?2019/3/1624板书设计 综合法证明不等式概念
应用
[例题3]
[例题4]
课堂练习
课时小结
课后作业2019/3/1625敬请多多指教星子实验中学
周 荣2019/3/1626敬请多多指教星子实验中学 周 荣
