简单几何体[上学期]
图片预览








文档简介
(共32张PPT)
简单几何体
1.平行线……线是平行的,可看起来却不是……
2.难道这些点是徘
徊在横纵间的灵魂 ,
一会消失,一会出
现 ……
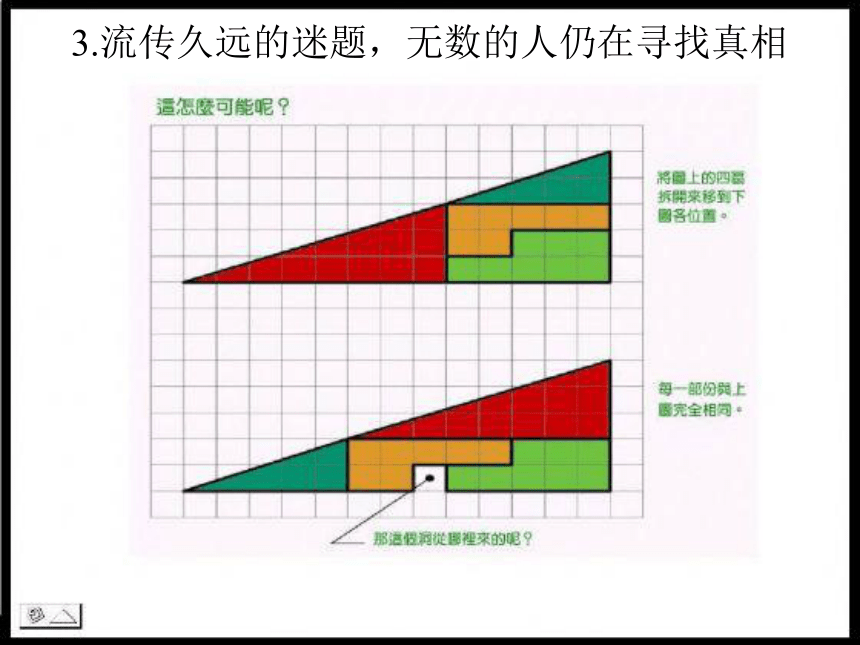
3.流传久远的迷题,无数的人仍在寻找真相
4、不相信火星木匠来过地球?看看这幅图吧,
这是唯一的证据 ……
5.绝对是静止的图片!你相信你的眼睛吗
学习立体几何时要注意:
不要太相信你自己的眼睛!
要多画图,从多个角度观察,
掌握图形的规律,发挥空间想象,
证明要有依有据。
生活中的几何体
一、球
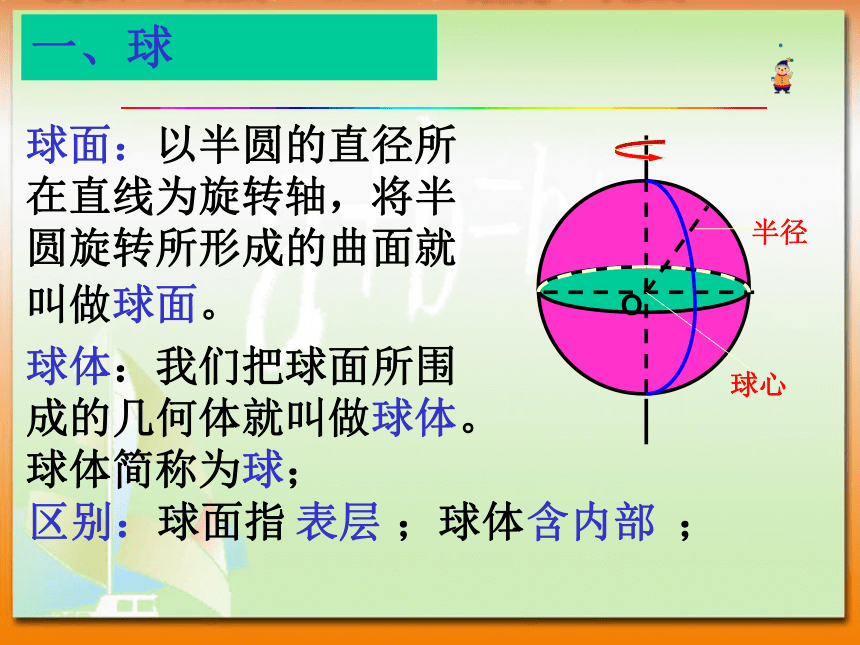
球面:以半圆的直径所在直线为旋转轴,将半圆旋转所形成的曲面就叫做球面。
球体:我们把球面所围成的几何体就叫做球体。球体简称为球;
区别:球面指 ;球体 ;
表层
含内部
O
半径
球心
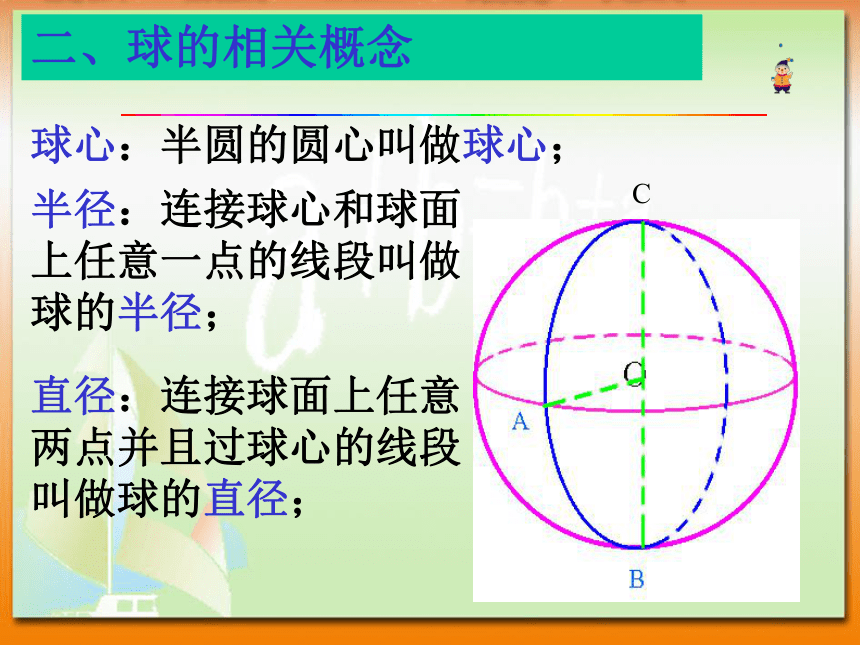
半径:连接球心和球面上任意一点的线段叫做球的半径;
直径:连接球面上任意两点并且过球心的线段叫做球的直径;
球心:半圆的圆心叫做球心;
二、球的相关概念
C
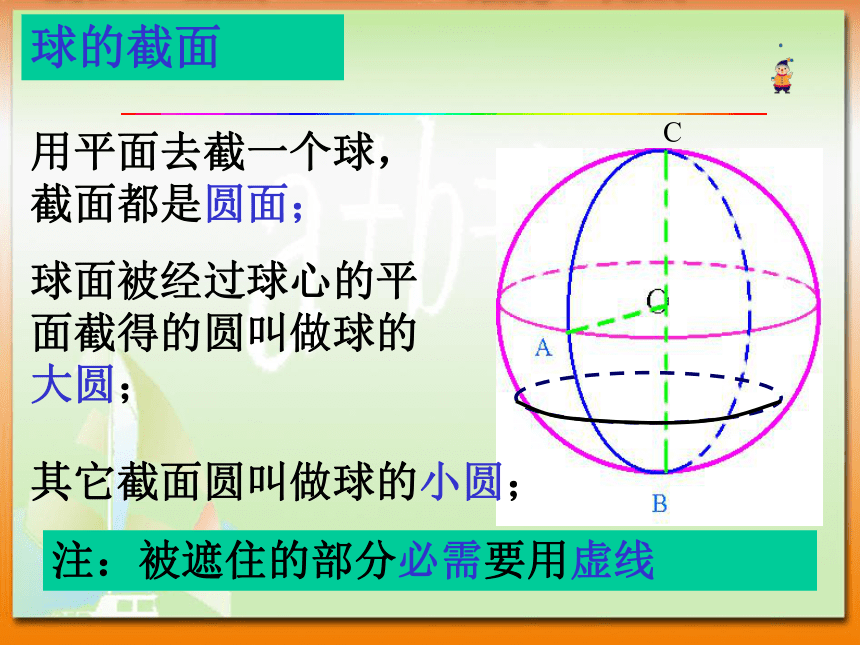
用平面去截一个球,截面都是圆面;
球的截面
球面被经过球心的平面截得的圆叫做球的大圆;
C
其它截面圆叫做球的小圆;
注:被遮住的部分必需要用虚线
在球面上,两点之间最短连线的长度,是经过这两点的大圆在两点间的劣弧的长度,称这段劣弧的长度为这
两点的球面距离;
球面距离
P
Q
M
N
放到同一
平面考虑
在球面上,两点之间最短连线的长度,是经过这两点的大圆在两点间的劣弧的长度,称这段劣弧的长度为这
两点的球面距离;
举例:
①飞机的飞行航线;
②轮船的航行路线;
球面距离
问:从中国上海飞往
美国洛杉机,途中经
美国夏威夷更近,还
是阿拉斯加?
南极
北极
0°
A
B
O1
O
上海
阿拉斯加
洛山矶
夏威夷群岛
B’
圆柱
A
A’
O
B
O’
轴
底面
侧面
母线
结构特征
以矩形的一边所在直线为旋转轴,其余边旋转形成的曲面所围成的几何体叫做圆柱。
圆锥
S
顶点
A
B
O
底面
轴
侧面
母线
结构特征
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥。
圆台
结构特征
O
O’
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.
二.简单多面体
D
A
B
C
E
F
F’
A’
E’
D’
B’
C’
棱柱
结构特征
有两个面互相平行,其余各面都是四边形,并且每相邻两个面的公共边都平行。
侧棱
侧面
底面
顶点
(1)底面互相平行。
(2)侧面是平行四边形。
棱锥
S
A
B
C
D
顶点
侧面
侧棱
底面
结构特征
有一个面是多边形,其余各面都是有一个公共顶点的三角形。
棱台
结构特征
A
B
C
D
A’
B’
C’
D’
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台.
五、课堂练习
1、口答:
①球、圆柱、圆锥、圆台过轴的截面(轴截面)分别是什么图形?
②斜棱柱的侧面中可能有矩形吗?
答:分别是:圆、矩形、等腰三角形、等腰梯形;
答:可能有矩形;
③图中的几何体是棱台吗?
不是棱台
是棱台
2、画出下列图形
①棱长为3cm的正方体;
②底边长为3cm,高为3cm的正四棱锥;
③半径为2cm的球;
C
注:遮住的部分必需要用虚线
④底半径为2cm,高为4cm的圆锥;
AOB为P点所在经线的经度
六、地球的经纬度
经线:半圆
纬线:整圆
AOC为C点所在纬线的纬度
C
地球的经度
某点的经度是经过这点的经线和地轴确定的半平面与0度经线(本初子午线)和地轴确定的半平面所成二面角的度数。
地球的纬度
AOP为 P点
所在纬线的纬度
有关地理知识
纬度:某点的纬度就是经过这点的球半径与赤道面所成角的度数.
地理知识
有关地理知识
八、课后作业
分别用尺规画出下列五个图形
4.棱长为3cm的正方体;
5.底边长为3cm,高为3cm的正四棱锥;
1.半径为2cm的球;
2.底半径为2cm,高为4cm的圆锥。
3.底边长为3cm,高为3cm的圆柱;
§2 三视图
九、预习提纲
简单几何体
1.平行线……线是平行的,可看起来却不是……
2.难道这些点是徘
徊在横纵间的灵魂 ,
一会消失,一会出
现 ……
3.流传久远的迷题,无数的人仍在寻找真相
4、不相信火星木匠来过地球?看看这幅图吧,
这是唯一的证据 ……
5.绝对是静止的图片!你相信你的眼睛吗
学习立体几何时要注意:
不要太相信你自己的眼睛!
要多画图,从多个角度观察,
掌握图形的规律,发挥空间想象,
证明要有依有据。
生活中的几何体
一、球
球面:以半圆的直径所在直线为旋转轴,将半圆旋转所形成的曲面就叫做球面。
球体:我们把球面所围成的几何体就叫做球体。球体简称为球;
区别:球面指 ;球体 ;
表层
含内部
O
半径
球心
半径:连接球心和球面上任意一点的线段叫做球的半径;
直径:连接球面上任意两点并且过球心的线段叫做球的直径;
球心:半圆的圆心叫做球心;
二、球的相关概念
C
用平面去截一个球,截面都是圆面;
球的截面
球面被经过球心的平面截得的圆叫做球的大圆;
C
其它截面圆叫做球的小圆;
注:被遮住的部分必需要用虚线
在球面上,两点之间最短连线的长度,是经过这两点的大圆在两点间的劣弧的长度,称这段劣弧的长度为这
两点的球面距离;
球面距离
P
Q
M
N
放到同一
平面考虑
在球面上,两点之间最短连线的长度,是经过这两点的大圆在两点间的劣弧的长度,称这段劣弧的长度为这
两点的球面距离;
举例:
①飞机的飞行航线;
②轮船的航行路线;
球面距离
问:从中国上海飞往
美国洛杉机,途中经
美国夏威夷更近,还
是阿拉斯加?
南极
北极
0°
A
B
O1
O
上海
阿拉斯加
洛山矶
夏威夷群岛
B’
圆柱
A
A’
O
B
O’
轴
底面
侧面
母线
结构特征
以矩形的一边所在直线为旋转轴,其余边旋转形成的曲面所围成的几何体叫做圆柱。
圆锥
S
顶点
A
B
O
底面
轴
侧面
母线
结构特征
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥。
圆台
结构特征
O
O’
用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分是圆台.
二.简单多面体
D
A
B
C
E
F
F’
A’
E’
D’
B’
C’
棱柱
结构特征
有两个面互相平行,其余各面都是四边形,并且每相邻两个面的公共边都平行。
侧棱
侧面
底面
顶点
(1)底面互相平行。
(2)侧面是平行四边形。
棱锥
S
A
B
C
D
顶点
侧面
侧棱
底面
结构特征
有一个面是多边形,其余各面都是有一个公共顶点的三角形。
棱台
结构特征
A
B
C
D
A’
B’
C’
D’
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台.
五、课堂练习
1、口答:
①球、圆柱、圆锥、圆台过轴的截面(轴截面)分别是什么图形?
②斜棱柱的侧面中可能有矩形吗?
答:分别是:圆、矩形、等腰三角形、等腰梯形;
答:可能有矩形;
③图中的几何体是棱台吗?
不是棱台
是棱台
2、画出下列图形
①棱长为3cm的正方体;
②底边长为3cm,高为3cm的正四棱锥;
③半径为2cm的球;
C
注:遮住的部分必需要用虚线
④底半径为2cm,高为4cm的圆锥;
AOB为P点所在经线的经度
六、地球的经纬度
经线:半圆
纬线:整圆
AOC为C点所在纬线的纬度
C
地球的经度
某点的经度是经过这点的经线和地轴确定的半平面与0度经线(本初子午线)和地轴确定的半平面所成二面角的度数。
地球的纬度
AOP为 P点
所在纬线的纬度
有关地理知识
纬度:某点的纬度就是经过这点的球半径与赤道面所成角的度数.
地理知识
有关地理知识
八、课后作业
分别用尺规画出下列五个图形
4.棱长为3cm的正方体;
5.底边长为3cm,高为3cm的正四棱锥;
1.半径为2cm的球;
2.底半径为2cm,高为4cm的圆锥。
3.底边长为3cm,高为3cm的圆柱;
§2 三视图
九、预习提纲
