人教版九年级上册22.1.4二次函数y=ax2 bx c的图象与性质课件(共20张PPT)
文档属性
| 名称 | 人教版九年级上册22.1.4二次函数y=ax2 bx c的图象与性质课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 419.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 07:16:56 | ||
图片预览







文档简介
(共20张PPT)
第二十二章 二次函数
22.1.4 二次函数y=ax2+bx+c(a≠0)图象和性质
人教版 九年级上册
学习目标
1.会画y=ax2+bx+c的图象;
2.理解y=ax2+bx+c的性质;
3.掌握y=ax2+bx+c与y=a(x-h)2+k的图象及性质的联系与区别.
请说出二次函数 y= 0.2(x+3)2 5 图象的开口方向,对称轴,顶点坐标.它是由y=-0.2x2怎样平移得到的?
知识回顾
y= 0.2(x+3)2 5 图象的开口方向向下,对称轴是直线x=-3,顶点为(-3,-5),由y=-0.2x2图象向左平移3个单位,再向下平移5个单位得到的.
配方化成顶点式
函数y=x2的图象,通过平移抛物线y=x2可以得到二次函数y=x2-6x+5的图象.
探究新知
怎样直接作出函数y=x2-6x+5的图象
y=x2-6x+5
探究新知
y=x2-6x+9-9+5
y=(x-3)2-4
哇!是不是很简单
y=x2-6x+5图象的开口方向向上,对称轴是直线x=3,顶点为(3,-4),由y=x2图象向右平移3个单位,再向下平移4个单位得到的.
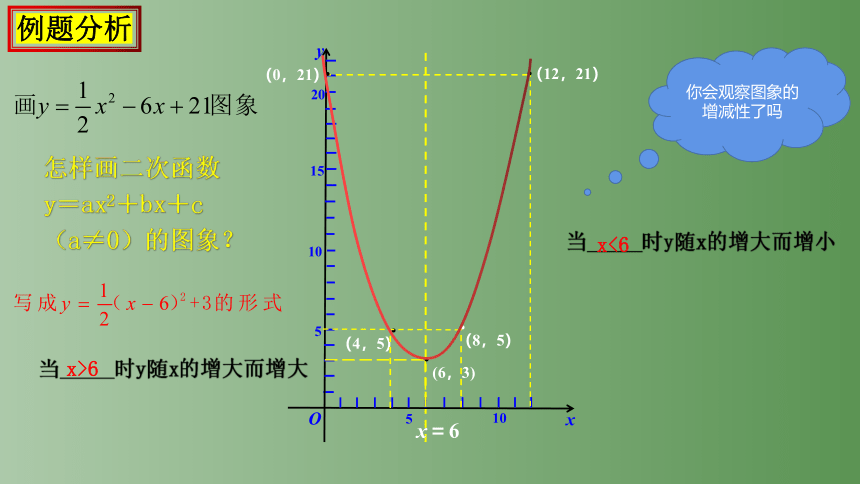
例题分析
1.提取二次项系数
2.配方:加上再减去一次项系数绝对值一半的平方
3.前三项化为完全平方式,后两项合并同类项
当_____时y随x的增大而增大
O
y
x
5
10
5
10
20
15
x=6
·
(6,3)
·
(8,5)
·
(4,5)
·
(0,21)
·
(12,21)
怎样画二次函数
y=ax2+bx+c(a≠0)的图象?
例题分析
你会观察图象的增减性了吗
当_____时y随x的增大而增小
x>6
x<6
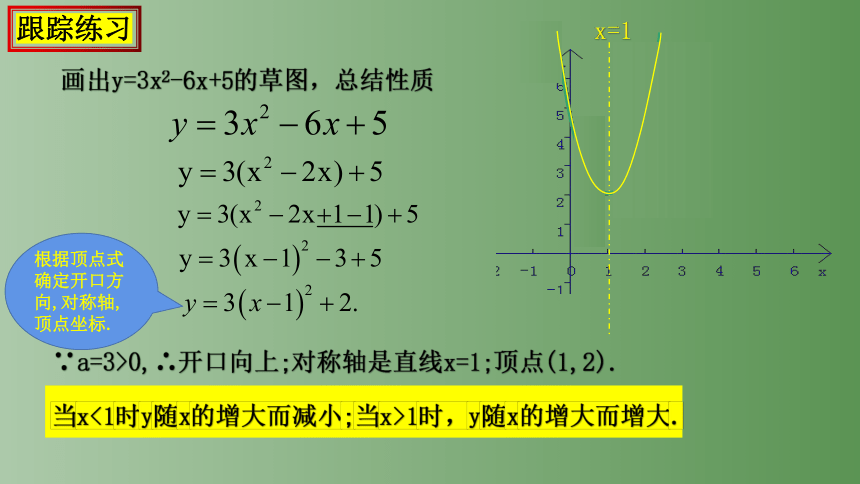
跟踪练习
画出y=3x2-6x+5的草图,总结性质
根据顶点式确定开口方向,对称轴,顶点坐标.
∵a=3>0,∴开口向上;对称轴是直线x=1;顶点(1,2).
当x<1时y随x的增大而减小;当x>1时,y随x的增大而增大.
x=1
提取二次项系数
配方:加上再减去一次项系数绝对值一半的平方
前三项化为平方形式,后两项合并同类项
对于二次函数y=ax +bx+c,可以利用配方法推导出它的对称轴和顶点坐标.
你能把函数y=ax +bx+c通过配方法化成y=a(x-h)2+k形式吗?
探究新知
叫抛物线的顶点式
抛物线的顶点式
二次函数y=ax +bx+c的图象是一条抛物线.
探究新知
这是求y=ax2+bx+c的顶点坐标和对称轴的公式,记住哟
对称轴是x=-1,顶点坐标是(-1,1)
对称轴是x=1,顶点坐标是(1,2)
对称轴是x=0,顶点坐标是(0,12)
根据公式确定下列二次函数图象的对称轴和顶点坐标:
跟踪练习
二次函数y=ax2+bx+c(a≠0)的图象和性质
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
向上
向下
在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
在对称轴的右侧, y随着x的增大而减小.
总结归纳
1.相同点: (1)形状相同(图象都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最大(或小)值.
(4)a>0时,开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
二次函数y=ax2+bx+c(a≠0)与y=ax 的关系
总结归纳
2.不同点:
(1)位置不同(2)顶点不同:分别是__________和(0,0).
(3)对称轴不同:分别是___________和y轴.
(4)最值不同:分别是_______和0.
3.联系: y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿
x轴整体左(右)平移____个单位(当___ 时,向右平移;当___
时,向左平移),再沿对称轴整体上(下)平移_____ 个单位
(当_____ _时向上平移;当_____ 时,向下平移)得到的.
总结归纳
(攀枝花中考)如图,二次函数y=ax2-bx+2的大致图象如图所示,则函数y=-ax+b的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
A
x
y
o
中考链接
1.抛物线y=-(x-2)2-1开口向 ,对称轴为 ,顶点坐标为________.
2.y=-2x2 -8x-6的顶点是 .可以看成由抛物线 向 平移 个单位得到的,再向 平移 个单位得到的.
下
x=2
(2,-1)
y=-2x2
左
2
当堂检测
上
2
(-2,2)
3.抛物线y=x2-10x +24可以看成由抛物线 向 平移
个单位得到的,再向 平移 个单位得到的.
y=x2
右
5
当堂检测
下
1
4.抛物线y=-x2-2x有最 值为______.
大
1
5.抛物线y=-x2+4x-3顶点坐标为( ).
A.(2,1) B.(-2,1)
C.(2,-1) D.(-2,-5)
A
6.有一喷水池,水从地面喷出,如图建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2-6x(单位:米)的一部分,则水喷出的最大高度是( )
A.10米 B.9米 C.8米 D.7米
x (米)
y (米)
B
当堂检测
7.已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
⑴求出b,c的值,并写出此时二次函数的解析式;
⑵根据图象,写出函数值y为正数时,自变量x的取值范围.
x
y
3
-1
O
解:⑴根据题意 得:
解得
所以抛物线的解析式为
⑵令
解得
根据图象可得当函数值y为正数时,自变量x的取值范围是
x
坚持就是胜利
第二十二章 二次函数
22.1.4 二次函数y=ax2+bx+c(a≠0)图象和性质
人教版 九年级上册
学习目标
1.会画y=ax2+bx+c的图象;
2.理解y=ax2+bx+c的性质;
3.掌握y=ax2+bx+c与y=a(x-h)2+k的图象及性质的联系与区别.
请说出二次函数 y= 0.2(x+3)2 5 图象的开口方向,对称轴,顶点坐标.它是由y=-0.2x2怎样平移得到的?
知识回顾
y= 0.2(x+3)2 5 图象的开口方向向下,对称轴是直线x=-3,顶点为(-3,-5),由y=-0.2x2图象向左平移3个单位,再向下平移5个单位得到的.
配方化成顶点式
函数y=x2的图象,通过平移抛物线y=x2可以得到二次函数y=x2-6x+5的图象.
探究新知
怎样直接作出函数y=x2-6x+5的图象
y=x2-6x+5
探究新知
y=x2-6x+9-9+5
y=(x-3)2-4
哇!是不是很简单
y=x2-6x+5图象的开口方向向上,对称轴是直线x=3,顶点为(3,-4),由y=x2图象向右平移3个单位,再向下平移4个单位得到的.
例题分析
1.提取二次项系数
2.配方:加上再减去一次项系数绝对值一半的平方
3.前三项化为完全平方式,后两项合并同类项
当_____时y随x的增大而增大
O
y
x
5
10
5
10
20
15
x=6
·
(6,3)
·
(8,5)
·
(4,5)
·
(0,21)
·
(12,21)
怎样画二次函数
y=ax2+bx+c(a≠0)的图象?
例题分析
你会观察图象的增减性了吗
当_____时y随x的增大而增小
x>6
x<6
跟踪练习
画出y=3x2-6x+5的草图,总结性质
根据顶点式确定开口方向,对称轴,顶点坐标.
∵a=3>0,∴开口向上;对称轴是直线x=1;顶点(1,2).
当x<1时y随x的增大而减小;当x>1时,y随x的增大而增大.
x=1
提取二次项系数
配方:加上再减去一次项系数绝对值一半的平方
前三项化为平方形式,后两项合并同类项
对于二次函数y=ax +bx+c,可以利用配方法推导出它的对称轴和顶点坐标.
你能把函数y=ax +bx+c通过配方法化成y=a(x-h)2+k形式吗?
探究新知
叫抛物线的顶点式
抛物线的顶点式
二次函数y=ax +bx+c的图象是一条抛物线.
探究新知
这是求y=ax2+bx+c的顶点坐标和对称轴的公式,记住哟
对称轴是x=-1,顶点坐标是(-1,1)
对称轴是x=1,顶点坐标是(1,2)
对称轴是x=0,顶点坐标是(0,12)
根据公式确定下列二次函数图象的对称轴和顶点坐标:
跟踪练习
二次函数y=ax2+bx+c(a≠0)的图象和性质
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
向上
向下
在对称轴的左侧,y随着x的增大而减小.
在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大.
在对称轴的右侧, y随着x的增大而减小.
总结归纳
1.相同点: (1)形状相同(图象都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最大(或小)值.
(4)a>0时,开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
二次函数y=ax2+bx+c(a≠0)与y=ax 的关系
总结归纳
2.不同点:
(1)位置不同(2)顶点不同:分别是__________和(0,0).
(3)对称轴不同:分别是___________和y轴.
(4)最值不同:分别是_______和0.
3.联系: y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿
x轴整体左(右)平移____个单位(当___ 时,向右平移;当___
时,向左平移),再沿对称轴整体上(下)平移_____ 个单位
(当_____ _时向上平移;当_____ 时,向下平移)得到的.
总结归纳
(攀枝花中考)如图,二次函数y=ax2-bx+2的大致图象如图所示,则函数y=-ax+b的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
A
x
y
o
中考链接
1.抛物线y=-(x-2)2-1开口向 ,对称轴为 ,顶点坐标为________.
2.y=-2x2 -8x-6的顶点是 .可以看成由抛物线 向 平移 个单位得到的,再向 平移 个单位得到的.
下
x=2
(2,-1)
y=-2x2
左
2
当堂检测
上
2
(-2,2)
3.抛物线y=x2-10x +24可以看成由抛物线 向 平移
个单位得到的,再向 平移 个单位得到的.
y=x2
右
5
当堂检测
下
1
4.抛物线y=-x2-2x有最 值为______.
大
1
5.抛物线y=-x2+4x-3顶点坐标为( ).
A.(2,1) B.(-2,1)
C.(2,-1) D.(-2,-5)
A
6.有一喷水池,水从地面喷出,如图建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2-6x(单位:米)的一部分,则水喷出的最大高度是( )
A.10米 B.9米 C.8米 D.7米
x (米)
y (米)
B
当堂检测
7.已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
⑴求出b,c的值,并写出此时二次函数的解析式;
⑵根据图象,写出函数值y为正数时,自变量x的取值范围.
x
y
3
-1
O
解:⑴根据题意 得:
解得
所以抛物线的解析式为
⑵令
解得
根据图象可得当函数值y为正数时,自变量x的取值范围是
x
坚持就是胜利
同课章节目录
