24.4.1弧长和扇形面积公式 课件(共28张PPT)
文档属性
| 名称 | 24.4.1弧长和扇形面积公式 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 16:52:42 | ||
图片预览






文档简介
(共28张PPT)
24.4.1弧长和扇形面积公式
人教版九年级上册
教学目标
教学目标:1.掌握弧长和扇形面积公式的探求过程.
2.会利用弧长和扇形面积的计算公式进行计算.
教学重点:掌握弧长和扇形面积公式的探求过程.
教学难点:会利用弧长和扇形面积的计算公式进行计算.
新知导入
情境引入
问题1 如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
问题2 怎样来计算弯道的“展直长度”?
因为要保证这些弯道的“展直长度”是一样的.
新知讲解
合作学习
想 一 想 :
圆心角是 的弧长度是多少?
3600
1800
1个圆周长
个圆周长
个圆周长
个圆周长
900
2700
半径是R,圆心角是1°的弧长是多少?
如 何 求 弧 长
合作探究
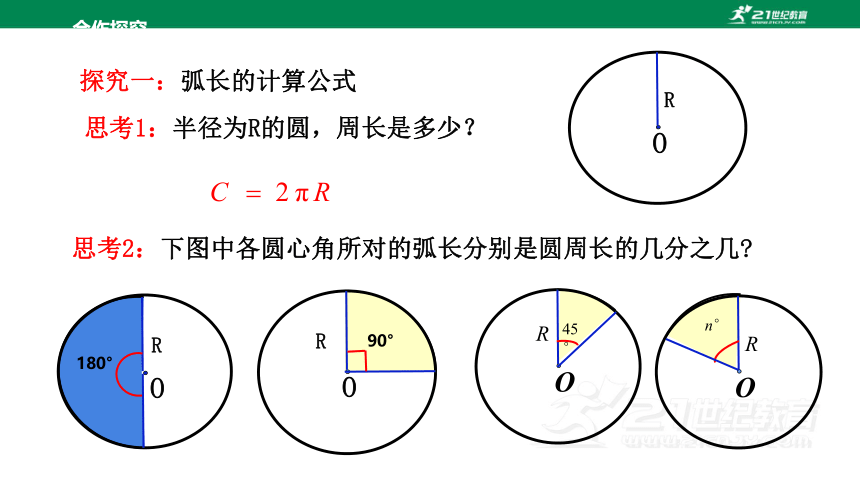
思考1:半径为R的圆,周长是多少?
O
R
思考2:下图中各圆心角所对的弧长分别是圆周长的几分之几
O
R
180°
O
R
90°
探究一:弧长的计算公式
O
R
45°
O
R
n°
(1) 圆心角是180°,占整个周角的 ,因此它所对的弧长是圆周长的__________.
(2) 圆心角是90°,占整个周角的 ,因此它所对的弧长是圆周长的__________.
(3) 圆心角是45°,占整个周角的 ,因此它所对的弧长是圆周长的__________.
(4) 圆心角是n°,占整个周角的 ,因此它所对的弧长是圆周长的__________.
提炼概念
特别强调:用弧长公式进行计算时,要注意公式中n的意义:n表示1°圆心角的倍数,它是不带单位的.
★弧长公式:
例如、已知弧所对的圆周角为60°,半径是4,则弧长为 .
合作探究
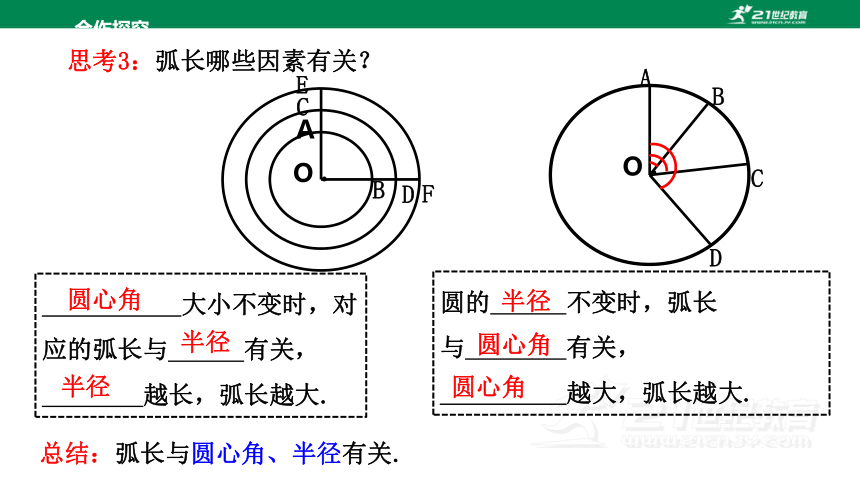
大小不变时,对应的弧长与 有关,
越长,弧长越大.
圆心角
半径
半径
圆的 不变时,弧长
与 有关,
越大,弧长越大.
圆心角
半径
圆心角
总结:弧长与圆心角、半径有关.
O ●
A
B
D
C
E
F
O ●
A
B
C
D
思考3:弧长哪些因素有关?
典例精讲
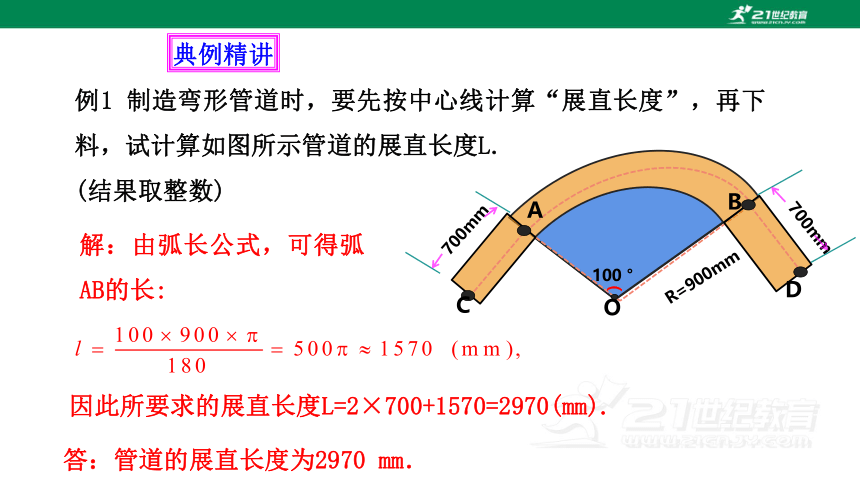
例1 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算如图所示管道的展直长度L.
(结果取整数)
解:由弧长公式,可得弧AB的长:
因此所要求的展直长度L=2×700+1570=2970(mm).
答:管道的展直长度为2970 mm.
700mm
700mm
R=900mm
(
100 °
A
C
B
D
O
探究二:扇形面积的计算公式
扇形的定义:圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫做扇形.
如图,黄色部分是一个扇形,记作扇形OAB.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
问题1 半径为r的圆,面积是多少?
O
r
问题2 下图中各扇形面积分别是圆面积的几分之几,具体是多少呢
圆心角占
周角的比例 扇形面积占
圆面积的比例 扇形的
面积
=
O
r
180°
O
r
90°
O
r
45°
O
r
n°
扇形面积公式
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
___大小不变时,对应的扇形面积与 有关,
___ 越长,面积越大.
圆心角
半径
半径
圆的 不变时,扇形面积与 有关,
越大,面积越大.
圆心角
半径
圆心角
总结:扇形的面积与圆心角、半径有关.
O ●
A
B
D
C
E
F
O ●
A
B
C
D
问题 扇形的面积与哪些因素有关?
例2 如图,水平放置的圆柱形排水管道的界面半径是0.6m,其中水面高0.3m.求截面上有水部分的面积(结果保留小数点后两位)
解:如图连接OA、OB,作弦AB的垂直平分线,垂足为D,交AB于点C,连接AC
∵OC=0.6m,DC=0.3m
∴OD=OC-DC=0.3m,
∴OD=DC
又∵AD⊥DC
∴AD是线段OC的垂直平分线
∴AC=AO=OC
从而∠AOD=60°,∠AOB=120°
有水部分的面积:S=S扇形OAB-S△OAB
=
=
=0.22(m2)
归纳概念
问题:扇形的弧长公式与面积公式有联系吗?
想一想 扇形的面积公式与什么公式类似?
A
B
O
O
课堂练习
1. 已知扇形的半径为6cm,圆心角为120°,则这个扇形的面积是( )
A. 36πcm2 B. 12πcm2 C. 9πcm2 D. 6πcm2
B
2.如果扇形的圆心角为150°,扇形面积为240πcm2,那么扇形的弧长为( )
A.5πcm B.10πcm
C.20πcm D.40πcm
C
3. 一个扇形的半径为18cm,弧长为9πcm,则此扇形的圆心角为_______.
90°
4. 如图,扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,求 的长是多少 贴纸部分的面积是多少
A
B
D
E
C
DE
解:∵ AB=30cm,BD=20cm
∴ AD=AB-BD=10cm
5.(例题变式题)如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
O
A
B
D
C
E
解:
6. 如图,正三角形 ABC 的边长为 a,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心, 长为半径作圆.求图中阴影部分的面积.
解:连接 AD
∵△ABC为正三角形
∴AB=BC=AC=a, ∠ABC=∠BCA=∠CAB=60°
∵D、E、F分别为BC、CA、AB的中点
∴AF=FB=BD=DC=CE=EA= , AD⊥BC
在Rt△ABD中根据勾股定理得,
课堂总结
弧长
计算公式:
扇形
定义
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.4.1弧长和扇形面积公式
人教版九年级上册
教学目标
教学目标:1.掌握弧长和扇形面积公式的探求过程.
2.会利用弧长和扇形面积的计算公式进行计算.
教学重点:掌握弧长和扇形面积公式的探求过程.
教学难点:会利用弧长和扇形面积的计算公式进行计算.
新知导入
情境引入
问题1 如图,在运动会的4×100米比赛中,甲和乙分别在第1跑道和第2跑道,为什么他们的起跑线不在同一处?
问题2 怎样来计算弯道的“展直长度”?
因为要保证这些弯道的“展直长度”是一样的.
新知讲解
合作学习
想 一 想 :
圆心角是 的弧长度是多少?
3600
1800
1个圆周长
个圆周长
个圆周长
个圆周长
900
2700
半径是R,圆心角是1°的弧长是多少?
如 何 求 弧 长
合作探究
思考1:半径为R的圆,周长是多少?
O
R
思考2:下图中各圆心角所对的弧长分别是圆周长的几分之几
O
R
180°
O
R
90°
探究一:弧长的计算公式
O
R
45°
O
R
n°
(1) 圆心角是180°,占整个周角的 ,因此它所对的弧长是圆周长的__________.
(2) 圆心角是90°,占整个周角的 ,因此它所对的弧长是圆周长的__________.
(3) 圆心角是45°,占整个周角的 ,因此它所对的弧长是圆周长的__________.
(4) 圆心角是n°,占整个周角的 ,因此它所对的弧长是圆周长的__________.
提炼概念
特别强调:用弧长公式进行计算时,要注意公式中n的意义:n表示1°圆心角的倍数,它是不带单位的.
★弧长公式:
例如、已知弧所对的圆周角为60°,半径是4,则弧长为 .
合作探究
大小不变时,对应的弧长与 有关,
越长,弧长越大.
圆心角
半径
半径
圆的 不变时,弧长
与 有关,
越大,弧长越大.
圆心角
半径
圆心角
总结:弧长与圆心角、半径有关.
O ●
A
B
D
C
E
F
O ●
A
B
C
D
思考3:弧长哪些因素有关?
典例精讲
例1 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算如图所示管道的展直长度L.
(结果取整数)
解:由弧长公式,可得弧AB的长:
因此所要求的展直长度L=2×700+1570=2970(mm).
答:管道的展直长度为2970 mm.
700mm
700mm
R=900mm
(
100 °
A
C
B
D
O
探究二:扇形面积的计算公式
扇形的定义:圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫做扇形.
如图,黄色部分是一个扇形,记作扇形OAB.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
问题1 半径为r的圆,面积是多少?
O
r
问题2 下图中各扇形面积分别是圆面积的几分之几,具体是多少呢
圆心角占
周角的比例 扇形面积占
圆面积的比例 扇形的
面积
=
O
r
180°
O
r
90°
O
r
45°
O
r
n°
扇形面积公式
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
___大小不变时,对应的扇形面积与 有关,
___ 越长,面积越大.
圆心角
半径
半径
圆的 不变时,扇形面积与 有关,
越大,面积越大.
圆心角
半径
圆心角
总结:扇形的面积与圆心角、半径有关.
O ●
A
B
D
C
E
F
O ●
A
B
C
D
问题 扇形的面积与哪些因素有关?
例2 如图,水平放置的圆柱形排水管道的界面半径是0.6m,其中水面高0.3m.求截面上有水部分的面积(结果保留小数点后两位)
解:如图连接OA、OB,作弦AB的垂直平分线,垂足为D,交AB于点C,连接AC
∵OC=0.6m,DC=0.3m
∴OD=OC-DC=0.3m,
∴OD=DC
又∵AD⊥DC
∴AD是线段OC的垂直平分线
∴AC=AO=OC
从而∠AOD=60°,∠AOB=120°
有水部分的面积:S=S扇形OAB-S△OAB
=
=
=0.22(m2)
归纳概念
问题:扇形的弧长公式与面积公式有联系吗?
想一想 扇形的面积公式与什么公式类似?
A
B
O
O
课堂练习
1. 已知扇形的半径为6cm,圆心角为120°,则这个扇形的面积是( )
A. 36πcm2 B. 12πcm2 C. 9πcm2 D. 6πcm2
B
2.如果扇形的圆心角为150°,扇形面积为240πcm2,那么扇形的弧长为( )
A.5πcm B.10πcm
C.20πcm D.40πcm
C
3. 一个扇形的半径为18cm,弧长为9πcm,则此扇形的圆心角为_______.
90°
4. 如图,扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,求 的长是多少 贴纸部分的面积是多少
A
B
D
E
C
DE
解:∵ AB=30cm,BD=20cm
∴ AD=AB-BD=10cm
5.(例题变式题)如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
O
A
B
D
C
E
解:
6. 如图,正三角形 ABC 的边长为 a,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心, 长为半径作圆.求图中阴影部分的面积.
解:连接 AD
∵△ABC为正三角形
∴AB=BC=AC=a, ∠ABC=∠BCA=∠CAB=60°
∵D、E、F分别为BC、CA、AB的中点
∴AF=FB=BD=DC=CE=EA= , AD⊥BC
在Rt△ABD中根据勾股定理得,
课堂总结
弧长
计算公式:
扇形
定义
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
