全国人教版数学九年级上册课课练:24.3正多边形和圆(含答案解析)
文档属性
| 名称 | 全国人教版数学九年级上册课课练:24.3正多边形和圆(含答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 449.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 09:17:44 | ||
图片预览

文档简介
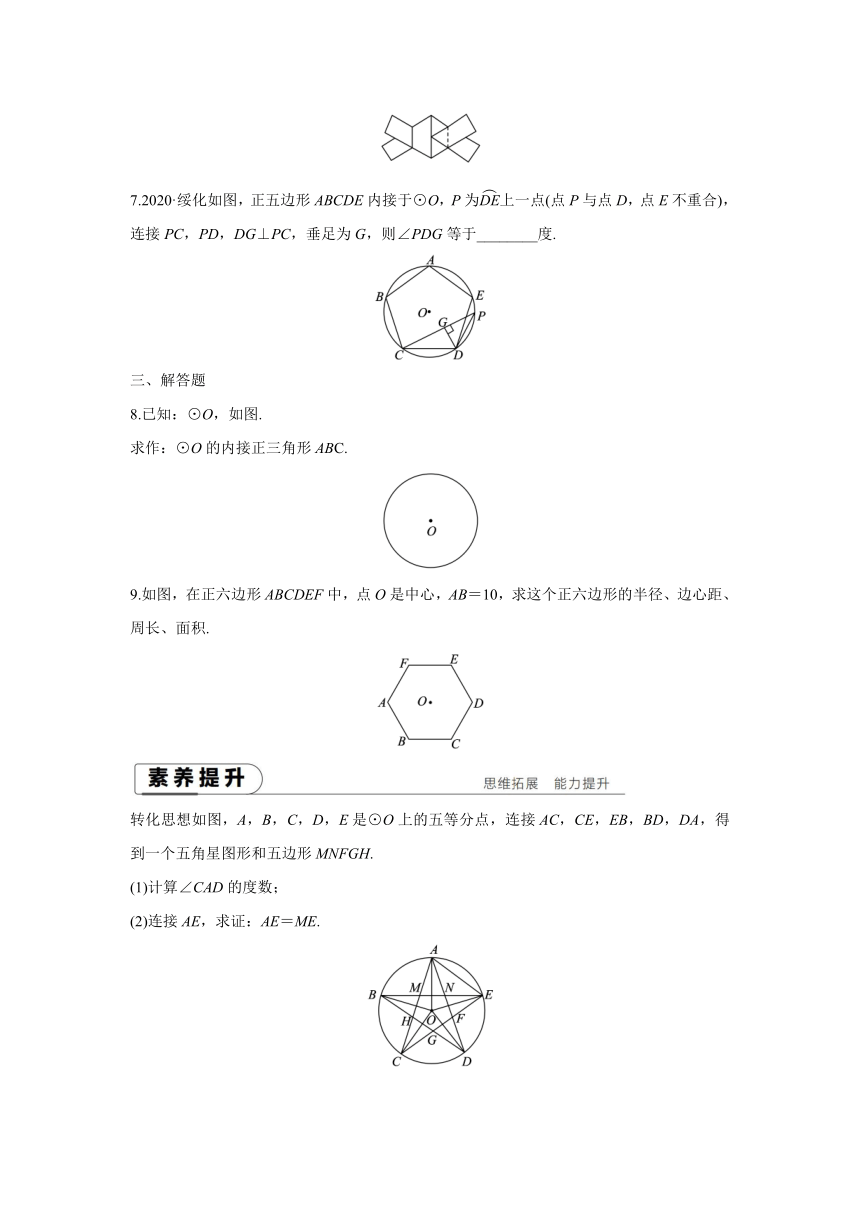
[正多边形和圆]
一、选择题
1.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
2.2019·湖州如图,已知正五边形ABCDE内接于⊙O,连接BD,则∠ABD的度数是( )
A.60° B.70° C.72° D.144°
3.2020·凉山州如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD∶AB等于( )
A.2 ∶ B.∶ C.∶ D.∶2
二、填空题
4.2020·扬州如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口b=3 cm,则螺帽的边长a=________ cm.
5.如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是________.
6.2019·衢州改编如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形,则原来的纸条宽为________.
7.2020·绥化如图,正五边形ABCDE内接于⊙O,P为上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,则∠PDG等于________度.
三、解答题
8.已知:⊙O,如图.
求作:⊙O的内接正三角形ABC.
9.如图,在正六边形ABCDEF中,点O是中心,AB=10,求这个正六边形的半径、边心距、周长、面积.
转化思想如图,A,B,C,D,E是⊙O上的五等分点,连接AC,CE,EB,BD,DA,得到一个五角星图形和五边形MNFGH.
(1)计算∠CAD的度数;
(2)连接AE,求证:AE=ME.
答案
1.A ∵正三角形一条边所对的圆心角是360°÷3=120°,
正方形一条边所对的圆心角是360°÷4=90°,
正五边形一条边所对的圆心角是360°÷5=72°,
正六边形一条边所对的圆心角是360°÷6=60°,
∴一条边所对的圆心角最大的图形是正三角形.
故选A.
2.C ∵正五边形ABCDE内接于⊙O,
∴∠ABC=∠C==108°,CB=CD,∴∠CBD=∠CDB==36°,
∴∠ABD=∠ABC-∠CBD=108°-36°=72°.
故选C.
3.B 如图,连接OA,OB,OD
则∠AOD=90°,∠AOB=120°.令OA=OB=OD=r,则AD=r,AB=r,
从而AD∶AB=∶.故选B.
4. 如图,连接AC,过点B作BD⊥AC于点D,
由螺帽是正六边形,得∠ABC=120°,AB=BC=a,
∴∠BCD=∠BAC=30°,∴BD=.由AC=3,得CD=1.5.由勾股定理可得a2=()2+1.52,
∴a=(负值已舍去).
5.8+8 易证四边形ABCD是正方形.
由题意可得AD=2+×2=2+2 ,
∴四边形ABCD的周长是4×(2+2 )=8+8 .故答案为8+8 .
6. 边长为2的正六边形由6个边长为2的等边三角形组成,其中等边三角形的高为原来的纸条宽度,所以原来的纸条宽度为.
7.54 连接CE.正五边形的内角∠CDE=×(5-2)×180°=108°.∵DC=DE,∴∠P=
∠DEC=×(180°-108°)=36°.
∵DG⊥PC,∴∠PDG=90°-∠P=54°.
8.解:方法一:先用圆规把圆周六等分,然后连接相间的三个分点,所得三角形即为所求(画图略).
方法二:(1)任意画一条半径OM;(2)作OM的垂直平分线交⊙O于点A,B;(3)以点A为圆心,以AB的长为半径画弧交⊙O于点C,连接AC,BC,则△ABC即为所求(画图略).
9.解:连接OB,OC,过点O作OH⊥BC于点H.∵正六边形的中心角为=60°,OB=OC,∴△OBC是等边三角形,
∴半径R=OB=BC=AB=10.
∵OH⊥BC,∴∠BOH=30°,∴BH=OB=5.
在Rt△OBH中,边心距r=OH==5 ,周长l=6AB=6×10=60.
∵S△OBC=BC·OH=×10×5 =25 ,
∴正六边形的面积S=6S△OBC=6×25 =150 .
[素养提升]
解:(1)∵A,B,C,D,E是⊙O上的五等分点,
∴∠COD==72°,
∴∠CAD=∠COD=36°.
(2)证明:∵A,B,C,D,E是⊙O上的五等分点,∴====,∴∠DAE=∠AEB=∠CAD=36°,∴∠MAE=72°,
∴∠AME=180°-∠MAE-∠AEB=72°=∠MAE,∴AE=ME.
一、选择题
1.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
2.2019·湖州如图,已知正五边形ABCDE内接于⊙O,连接BD,则∠ABD的度数是( )
A.60° B.70° C.72° D.144°
3.2020·凉山州如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD∶AB等于( )
A.2 ∶ B.∶ C.∶ D.∶2
二、填空题
4.2020·扬州如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口b=3 cm,则螺帽的边长a=________ cm.
5.如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是________.
6.2019·衢州改编如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形,则原来的纸条宽为________.
7.2020·绥化如图,正五边形ABCDE内接于⊙O,P为上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,则∠PDG等于________度.
三、解答题
8.已知:⊙O,如图.
求作:⊙O的内接正三角形ABC.
9.如图,在正六边形ABCDEF中,点O是中心,AB=10,求这个正六边形的半径、边心距、周长、面积.
转化思想如图,A,B,C,D,E是⊙O上的五等分点,连接AC,CE,EB,BD,DA,得到一个五角星图形和五边形MNFGH.
(1)计算∠CAD的度数;
(2)连接AE,求证:AE=ME.
答案
1.A ∵正三角形一条边所对的圆心角是360°÷3=120°,
正方形一条边所对的圆心角是360°÷4=90°,
正五边形一条边所对的圆心角是360°÷5=72°,
正六边形一条边所对的圆心角是360°÷6=60°,
∴一条边所对的圆心角最大的图形是正三角形.
故选A.
2.C ∵正五边形ABCDE内接于⊙O,
∴∠ABC=∠C==108°,CB=CD,∴∠CBD=∠CDB==36°,
∴∠ABD=∠ABC-∠CBD=108°-36°=72°.
故选C.
3.B 如图,连接OA,OB,OD
则∠AOD=90°,∠AOB=120°.令OA=OB=OD=r,则AD=r,AB=r,
从而AD∶AB=∶.故选B.
4. 如图,连接AC,过点B作BD⊥AC于点D,
由螺帽是正六边形,得∠ABC=120°,AB=BC=a,
∴∠BCD=∠BAC=30°,∴BD=.由AC=3,得CD=1.5.由勾股定理可得a2=()2+1.52,
∴a=(负值已舍去).
5.8+8 易证四边形ABCD是正方形.
由题意可得AD=2+×2=2+2 ,
∴四边形ABCD的周长是4×(2+2 )=8+8 .故答案为8+8 .
6. 边长为2的正六边形由6个边长为2的等边三角形组成,其中等边三角形的高为原来的纸条宽度,所以原来的纸条宽度为.
7.54 连接CE.正五边形的内角∠CDE=×(5-2)×180°=108°.∵DC=DE,∴∠P=
∠DEC=×(180°-108°)=36°.
∵DG⊥PC,∴∠PDG=90°-∠P=54°.
8.解:方法一:先用圆规把圆周六等分,然后连接相间的三个分点,所得三角形即为所求(画图略).
方法二:(1)任意画一条半径OM;(2)作OM的垂直平分线交⊙O于点A,B;(3)以点A为圆心,以AB的长为半径画弧交⊙O于点C,连接AC,BC,则△ABC即为所求(画图略).
9.解:连接OB,OC,过点O作OH⊥BC于点H.∵正六边形的中心角为=60°,OB=OC,∴△OBC是等边三角形,
∴半径R=OB=BC=AB=10.
∵OH⊥BC,∴∠BOH=30°,∴BH=OB=5.
在Rt△OBH中,边心距r=OH==5 ,周长l=6AB=6×10=60.
∵S△OBC=BC·OH=×10×5 =25 ,
∴正六边形的面积S=6S△OBC=6×25 =150 .
[素养提升]
解:(1)∵A,B,C,D,E是⊙O上的五等分点,
∴∠COD==72°,
∴∠CAD=∠COD=36°.
(2)证明:∵A,B,C,D,E是⊙O上的五等分点,∴====,∴∠DAE=∠AEB=∠CAD=36°,∴∠MAE=72°,
∴∠AME=180°-∠MAE-∠AEB=72°=∠MAE,∴AE=ME.
同课章节目录
