人教版数学九年级上册课课练:24.1.3弧、弦、圆心角(Word版含答案解析)
文档属性
| 名称 | 人教版数学九年级上册课课练:24.1.3弧、弦、圆心角(Word版含答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 289.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 09:21:54 | ||
图片预览

文档简介
[弧、弦、圆心角]
一、选择题
1.下列说法中正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,它们所对的弦也相等 D.等弦所对的圆心角相等
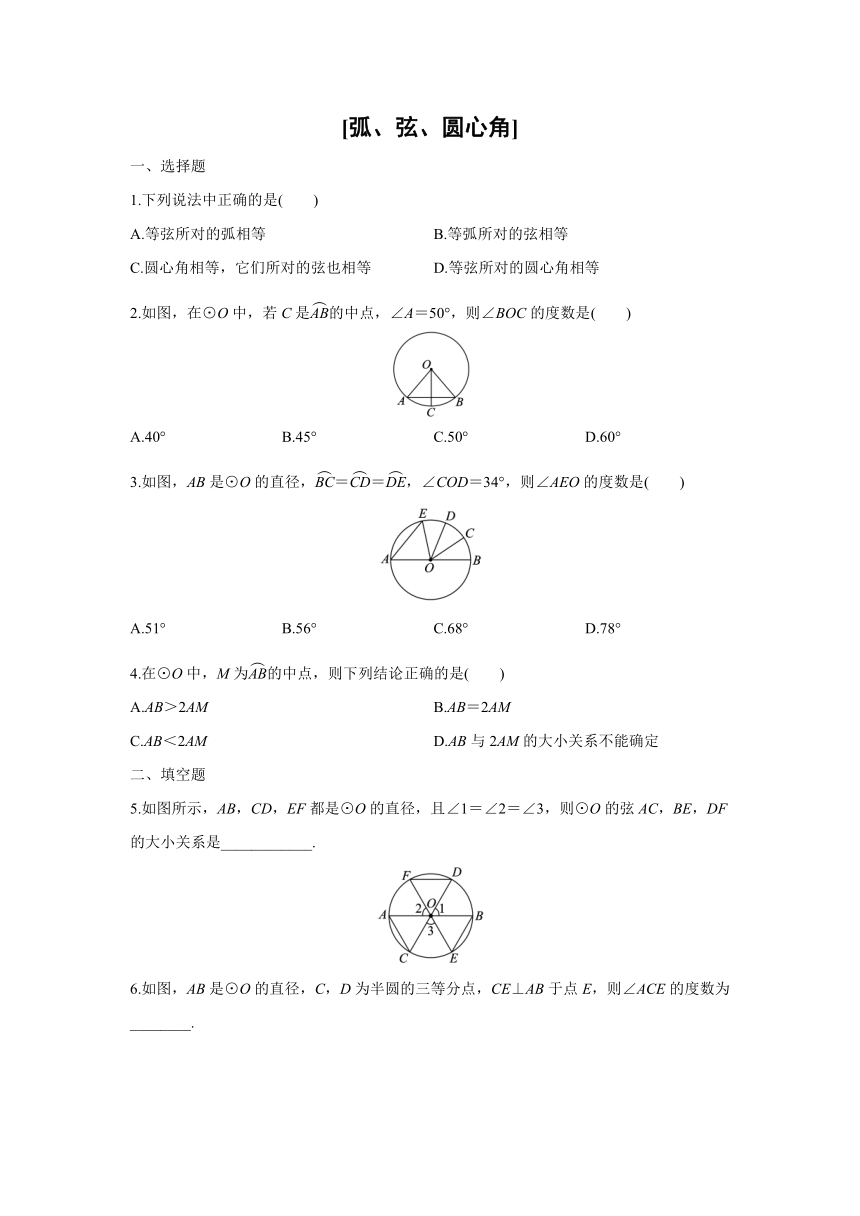
2.如图,在⊙O中,若C是的中点,∠A=50°,则∠BOC的度数是( )
A.40° B.45° C.50° D.60°
3.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )
A.51° B.56° C.68° D.78°
4.在⊙O中,M为的中点,则下列结论正确的是( )
A.AB>2AM B.AB=2AM
C.AB<2AM D.AB与2AM的大小关系不能确定
二、填空题
5.如图所示,AB,CD,EF都是⊙O的直径,且∠1=∠2=∠3,则⊙O的弦AC,BE,DF的大小关系是____________.
6.如图,AB是⊙O的直径,C,D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为________.
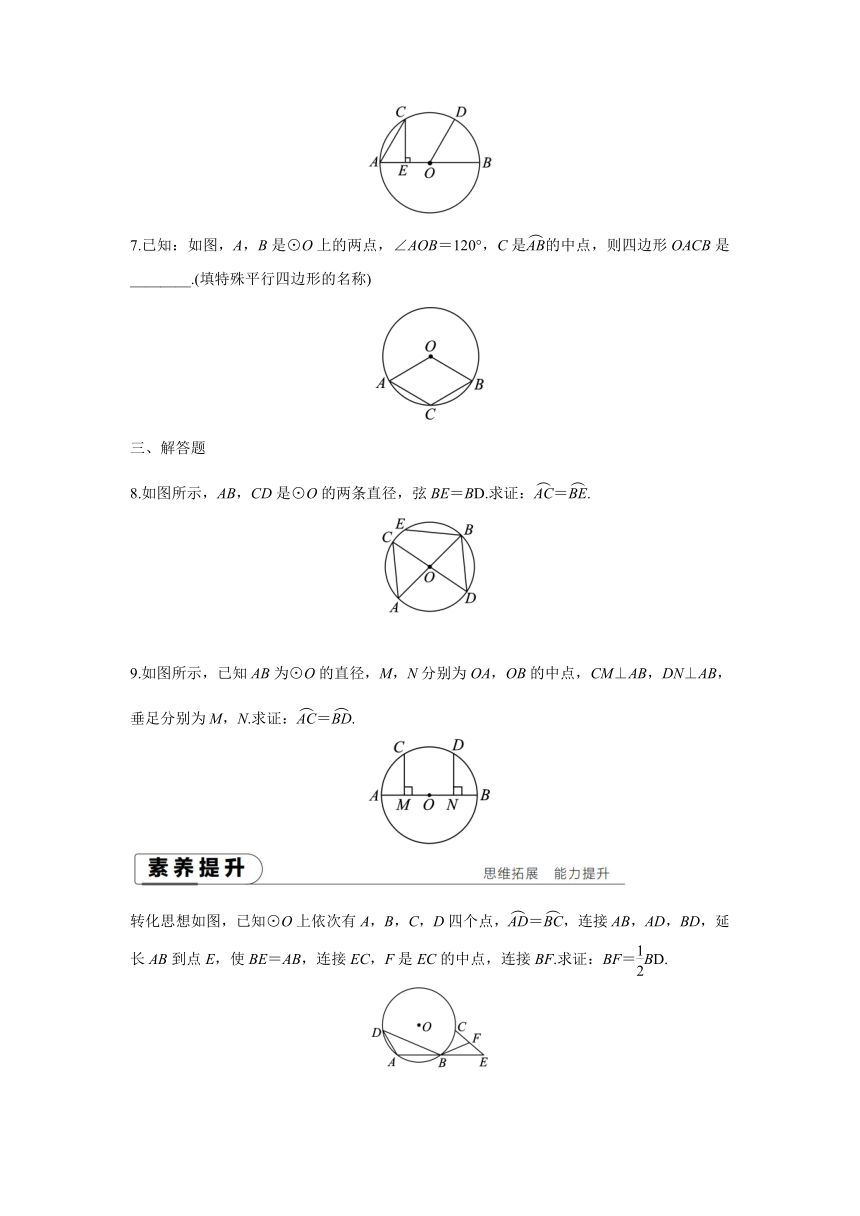
7.已知:如图,A,B是⊙O上的两点,∠AOB=120°,C是的中点,则四边形OACB是________.(填特殊平行四边形的名称)
三、解答题
8.如图所示,AB,CD是⊙O的两条直径,弦BE=BD.求证:=.
9.如图所示,已知AB为⊙O的直径,M,N分别为OA,OB的中点,CM⊥AB,DN⊥AB,垂足分别为M,N.求证:=.
转化思想如图,已知⊙O上依次有A,B,C,D四个点,=,连接AB,AD,BD,延长AB到点E,使BE=AB,连接EC,F是EC的中点,连接BF.求证:BF=BD.
答案
1.B
2.A ∵∠A=50°,OA=OB,
∴∠B=∠A=50°,
∴∠AOB=180°-50°-50°=80°.
∵C是的中点,
∴∠BOC=∠AOB=40°.
故选A.
3.A ∵==,∠COD=34°,
∴∠BOC=∠COD=∠EOD=34°,
∴∠AOE=180°-∠EOD-∠COD-∠BOC=78°.
又∵OA=OE,∴∠AEO=∠OAE,
∴∠AEO=×(180°-78°)=51°.
4.C 如图,
∵M为的中点,∴AM=BM.
∵AM+BM>AB,
∴AB<2AM.故选C.
5.AC=BE=DF
6.30° 连接OC.∵C,D为半圆的三等分点,∴∠AOC=∠AOB=60°.
又∵OA=OC,∴△AOC是等边三角形,
∴∠A=60°.
∵CE⊥AB,∴∠ACE=30°.
7.菱形 连接OC.
∵C是的中点,
∴∠AOC=∠COB=60°.
又∵OA=OC=OB,
∴△OAC和△OCB都是等边三角形,
∴OA=AC=BC=OB,
∴四边形OACB是菱形.
8.证明:∵AB,CD是⊙O的两条直径,
∴∠AOC=∠BOD,∴AC=BD.
又∵BE=BD,∴AC=BE,
∴=.
9.证明:连接OC,OD,如图.
∵OA=OB,M,N分别为OA,OB的中点,
∴OM=ON.
在Rt△COM和Rt△DON中,
∴Rt△COM≌Rt△DON,
∴∠COM=∠DON,∴=.
[素养提升]
证明:连接AC.
∵AB=BE,F是EC的中点,
∴BF是△EAC的中位线,∴BF=AC.
∵=,
∴+=+,即=,∴BD=AC,
∴BF=BD.
一、选择题
1.下列说法中正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,它们所对的弦也相等 D.等弦所对的圆心角相等
2.如图,在⊙O中,若C是的中点,∠A=50°,则∠BOC的度数是( )
A.40° B.45° C.50° D.60°
3.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )
A.51° B.56° C.68° D.78°
4.在⊙O中,M为的中点,则下列结论正确的是( )
A.AB>2AM B.AB=2AM
C.AB<2AM D.AB与2AM的大小关系不能确定
二、填空题
5.如图所示,AB,CD,EF都是⊙O的直径,且∠1=∠2=∠3,则⊙O的弦AC,BE,DF的大小关系是____________.
6.如图,AB是⊙O的直径,C,D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为________.
7.已知:如图,A,B是⊙O上的两点,∠AOB=120°,C是的中点,则四边形OACB是________.(填特殊平行四边形的名称)
三、解答题
8.如图所示,AB,CD是⊙O的两条直径,弦BE=BD.求证:=.
9.如图所示,已知AB为⊙O的直径,M,N分别为OA,OB的中点,CM⊥AB,DN⊥AB,垂足分别为M,N.求证:=.
转化思想如图,已知⊙O上依次有A,B,C,D四个点,=,连接AB,AD,BD,延长AB到点E,使BE=AB,连接EC,F是EC的中点,连接BF.求证:BF=BD.
答案
1.B
2.A ∵∠A=50°,OA=OB,
∴∠B=∠A=50°,
∴∠AOB=180°-50°-50°=80°.
∵C是的中点,
∴∠BOC=∠AOB=40°.
故选A.
3.A ∵==,∠COD=34°,
∴∠BOC=∠COD=∠EOD=34°,
∴∠AOE=180°-∠EOD-∠COD-∠BOC=78°.
又∵OA=OE,∴∠AEO=∠OAE,
∴∠AEO=×(180°-78°)=51°.
4.C 如图,
∵M为的中点,∴AM=BM.
∵AM+BM>AB,
∴AB<2AM.故选C.
5.AC=BE=DF
6.30° 连接OC.∵C,D为半圆的三等分点,∴∠AOC=∠AOB=60°.
又∵OA=OC,∴△AOC是等边三角形,
∴∠A=60°.
∵CE⊥AB,∴∠ACE=30°.
7.菱形 连接OC.
∵C是的中点,
∴∠AOC=∠COB=60°.
又∵OA=OC=OB,
∴△OAC和△OCB都是等边三角形,
∴OA=AC=BC=OB,
∴四边形OACB是菱形.
8.证明:∵AB,CD是⊙O的两条直径,
∴∠AOC=∠BOD,∴AC=BD.
又∵BE=BD,∴AC=BE,
∴=.
9.证明:连接OC,OD,如图.
∵OA=OB,M,N分别为OA,OB的中点,
∴OM=ON.
在Rt△COM和Rt△DON中,
∴Rt△COM≌Rt△DON,
∴∠COM=∠DON,∴=.
[素养提升]
证明:连接AC.
∵AB=BE,F是EC的中点,
∴BF是△EAC的中位线,∴BF=AC.
∵=,
∴+=+,即=,∴BD=AC,
∴BF=BD.
同课章节目录
