人教版数学九年级上册课课练:23章 常见的四种旋转“背景”(Word版含答案解析)
文档属性
| 名称 | 人教版数学九年级上册课课练:23章 常见的四种旋转“背景”(Word版含答案解析) | 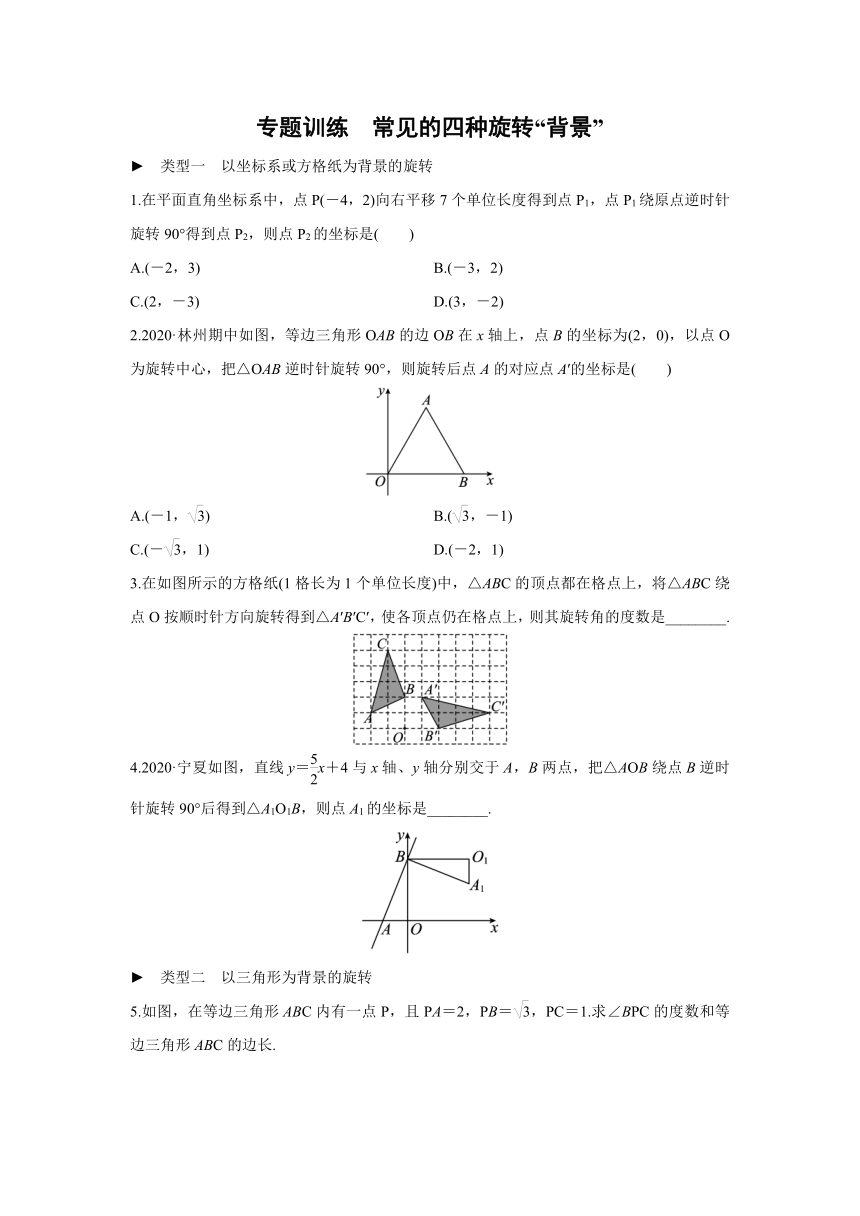 | |
| 格式 | docx | ||
| 文件大小 | 427.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 09:25:45 | ||
图片预览




文档简介
专题训练 常见的四种旋转“背景”
类型一 以坐标系或方格纸为背景的旋转
1.在平面直角坐标系中,点P(-4,2)向右平移7个单位长度得到点P1,点P1绕原点逆时针旋转90°得到点P2,则点P2的坐标是( )
A.(-2,3) B.(-3,2)
C.(2,-3) D.(3,-2)
2.2020·林州期中如图,等边三角形OAB的边OB在x轴上,点B的坐标为(2,0),以点O为旋转中心,把△OAB逆时针旋转90°,则旋转后点A的对应点A′的坐标是( )
A.(-1,) B.(,-1)
C.(-,1) D.(-2,1)
3.在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A′B′C′,使各顶点仍在格点上,则其旋转角的度数是________.
4.2020·宁夏如图,直线y=x+4与x轴、y轴分别交于A,B两点,把△AOB绕点B逆时针旋转90°后得到△A1O1B,则点A1的坐标是________.
类型二 以三角形为背景的旋转
5.如图,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1.求∠BPC的度数和等边三角形ABC的边长.
6.如图①是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.
(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长;
②当A,D,M三点为同一直角三角形的顶点时,求AM的长.
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外部的点D1处转到其内部的点D2处,连接D1D2,如图②,此时∠AD2C=135°,CD2=60,求BD2的长.
类型三 以四边形为背景的旋转
7.2020·萍乡期末【课题研究】旋转图形中对应线段所在直线的夹角(小于等于90°的角)与旋转角的关系.
【问题初探】线段AB绕点O顺时针旋转得到线段CD,其中点A与点C对应,点B与点D对应,旋转角的度数为α,且0°<α<180°.
(1)如图①,当α=60°时,线段AB,CD所在直线的夹角(锐角)为______________;
(2)如图②,当90°<α<180°时,直线AB与直线CD所夹锐角与旋转角α存在怎样的数量关系?请说明理由;
【形成结论】旋转图形中,当旋转角小于平角时,对应线段所在直线的夹角(小于等于90°的角)与旋转角________.
【运用拓广】运用所形成的结论解决问题:
如图③,在四边形ABCD中,∠ABC=60°,∠ADC=30°,AB=BC,CD=3,BD=,求AD的长.
类型四 以中点为背景的旋转
8.(1)如图(a),在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;
②若∠A=90°,探索线段BE,CF,EF之间的数量关系,并加以证明.
(2)如图(b),在四边形ABDC中,∠B+∠C=180°,BD=CD,∠BDC=120°,以D为顶点作一个60°的角,角的两边分别交AB,AC于E,F两点,连接EF,探索线段BE,CF,EF之间的数量关系,并加以证明.
答案
1.A 点P(-4,2)向右平移7个单位长度得到点P1(3,2),点P1绕原点逆时针旋转90°得到点P2(-2,3).故选A.
2.C
如图,过点A作AE⊥OB于点E,过点A′作A′H⊥x轴于点H.
∵B(2,0),△OAB是等边三角形,
∴OA=OB=AB=2.
∵AE⊥OB,
∴OE=EB=1,
∴AE===.
∵以点O为旋转中心把△OAB逆时针旋转90°,旋转后点A的对应点为A′,A′H⊥OH,
∴∠A′HO=∠OEA=∠AOA′=90°,OA′=OA,
∴∠A′OH+∠AOE=90°,∠AOE+∠OAE=90°,
∴∠A′OH=∠OAE,
∴△A′OH≌△OAE(AAS),
∴A′H=OE=1,OH=AE=,
∴A′(-,1).
故选C.
3.90° 找到一组对应点A,A′,并将其与旋转中心连接起来,确定旋转角,进而得到旋转角的度数为90°.
4.(4,) 在y=x+4中,令x=0,得y=4;
令y=0,得0=x+4,解得x=-,
∴A(-,0),B(0,4).
由旋转可得△AOB≌△A1O1B,∠ABA1=90°,
∴∠ABO=∠A1BO1,∠BO1A1=∠BOA=90°,O1A1=OA=,O1B=OB=4,
∴∠OBO1=90°,
∴O1B∥x轴,
∴点A1的纵坐标为OB-O1A1的长,
即4-=,
横坐标为O1B=4,
故点A1的坐标是(4,).
5.解:将△BPC绕点B逆时针旋转60°得到△BP′A(如图).
连接PP′,由旋转的性质知△BPP′为等边三角形,∠BP′A=∠BPC,AP′=PC=1,
∴PP′=PB=,∠BPP′=∠BP′P=60°.
在△APP′中,∵AP′2+PP′2=12+()2=22=PA2,
∴△APP′是直角三角形,且∠AP′P=90°,
∴∠BP′A=∠BP′P+∠AP′P=60°+90°=150°,
∴∠BPC=∠BP′A=150°.
在Rt△APP′中,∵PA=2,AP′=1,
∴∠APP′=30°.
又∵∠BPP′=60°,∴∠APB=90°,
∴在Rt△ABP中,AB===,
即等边三角形ABC的边长为.
6.解:(1)①当A,D,M三点在同一直线上时,AM=AD+DM=40或AM=AD-DM=20.
②当A,D,M三点为同一直角三角形的顶点时,显然∠MAD不能为直角.
当∠AMD为直角时,AM2=AD2-DM2=302-102=800.
∵AM>0,
∴AM=20 .
当∠ADM=90°时,AM2=AD2+DM2=302+102=1000.
∵AM>0,
∴AM=10 .
综上所述,满足条件的AM的长为20 或10 .
(2)如图,连接CD1.
由题意,得∠D1AD2=90°,AD1=AD2=30,
∴∠AD2D1=45°,D1D2=30 .
∵∠AD2C=135°,
∴∠CD2D1=∠AD2C-∠AD2D1=90°,
∴CD1==30 .
∵∠BAC=∠D1AD2=90°,
∴∠BAC-∠CAD2=∠D1AD2-∠CAD2,
即∠BAD2=∠CAD1.
又∵AB=AC,AD2=AD1,
∴△BAD2≌△CAD1(SAS),
∴BD2=CD1=30 .
7.解:【问题初探】
(1)60° 如图①,延长DC交AB于点F,交BO于点E.
∵α=60°,
∴∠BOD=60°.
∵线段AB绕点O顺时针旋转得到线段CD,
∴AB=CD,OA=OC,BO=DO,
∴△AOB≌△COD(SSS),
∴∠B=∠D.
又∵∠OED=∠BEF,
∴∠BFE=∠EOD=60°.
(2)直线AB与直线CD所夹锐角与旋转角α互补.
理由如图下:
如图②,延长AB,DC交于点E.
∵线段AB绕点O顺时针旋转得到线段CD,
∴AB=CD,OA=OC,BO=DO,
∴△AOB≌△COD(SSS),
∴∠ABO=∠D.
∵∠ABO+∠EBO=180°,
∴∠D+∠EBO=180°.
又∵∠EBO+∠E+∠D+∠BOD=360°,
∴∠E+∠BOD=180°,
∴直线AB与直线CD所夹锐角与旋转角α互补.
【形成结论】相等或互补
【运用拓广】如图③,将△BCD绕点B顺时针旋转60°,得到△BAF,连接FD,延长FA,DC交于点E.
∵旋转角∠ABC=60°,
∴由【形成结论】可知∠AED=∠ABC=60°.
由旋转的性质可知AF=CD=3,BD=BF.
∵∠ADC=30°,
∴∠FAD=∠AED+∠ADC=90°.
∵∠FBD=∠ABC=60°,BF=BD,
∴△BFD是等边三角形,
∴DF=BF=BD=,
∴在Rt△DAF中,AD===.
8.解:(1)①证明:如图(a),将△DBE绕点D旋转180°得到△DCG,连接FG,则△DCG≌△DBE,
∴DG=DE,CG=BE.
又∵DE⊥DF,
∴DF垂直平分线段EG,∴FG=EF.
∵在△CFG中,CG+CF>FG,
∴BE+CF>EF.
②BE2+CF2=EF2.
证明:∵∠A=90°,∴∠B+∠ACD=90°.
由①可得,∠FCG=∠FCD+∠DCG=∠FCD+∠B=90°,
∴在Rt△CFG中,由勾股定理,得CG2+CF2=FG2,∴BE2+CF2=EF2.
(2)EF=BE+CF.
证明:如图(b).∵CD=BD,∠BDC=120°,
∴将△CDF绕点D逆时针旋转120°可得到△BDM,
∴△BDM≌△CDF,
∴DM=DF,BM=CF,∠BDM=∠CDF,∠DBM=∠C.
∵∠ABD+∠C=180°,
∴∠ABD+∠DBM=180°,
∴点A,B,M共线,
∴∠EDM=∠EDB+∠BDM=∠EDB+∠CDF=∠BDC-∠EDF=120°-60°=60°=∠EDF.
在△DEM和△DEF中,
∴△DEM≌△DEF,
∴EF=EM=BE+BM=BE+CF.
类型一 以坐标系或方格纸为背景的旋转
1.在平面直角坐标系中,点P(-4,2)向右平移7个单位长度得到点P1,点P1绕原点逆时针旋转90°得到点P2,则点P2的坐标是( )
A.(-2,3) B.(-3,2)
C.(2,-3) D.(3,-2)
2.2020·林州期中如图,等边三角形OAB的边OB在x轴上,点B的坐标为(2,0),以点O为旋转中心,把△OAB逆时针旋转90°,则旋转后点A的对应点A′的坐标是( )
A.(-1,) B.(,-1)
C.(-,1) D.(-2,1)
3.在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A′B′C′,使各顶点仍在格点上,则其旋转角的度数是________.
4.2020·宁夏如图,直线y=x+4与x轴、y轴分别交于A,B两点,把△AOB绕点B逆时针旋转90°后得到△A1O1B,则点A1的坐标是________.
类型二 以三角形为背景的旋转
5.如图,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1.求∠BPC的度数和等边三角形ABC的边长.
6.如图①是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.
(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长;
②当A,D,M三点为同一直角三角形的顶点时,求AM的长.
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外部的点D1处转到其内部的点D2处,连接D1D2,如图②,此时∠AD2C=135°,CD2=60,求BD2的长.
类型三 以四边形为背景的旋转
7.2020·萍乡期末【课题研究】旋转图形中对应线段所在直线的夹角(小于等于90°的角)与旋转角的关系.
【问题初探】线段AB绕点O顺时针旋转得到线段CD,其中点A与点C对应,点B与点D对应,旋转角的度数为α,且0°<α<180°.
(1)如图①,当α=60°时,线段AB,CD所在直线的夹角(锐角)为______________;
(2)如图②,当90°<α<180°时,直线AB与直线CD所夹锐角与旋转角α存在怎样的数量关系?请说明理由;
【形成结论】旋转图形中,当旋转角小于平角时,对应线段所在直线的夹角(小于等于90°的角)与旋转角________.
【运用拓广】运用所形成的结论解决问题:
如图③,在四边形ABCD中,∠ABC=60°,∠ADC=30°,AB=BC,CD=3,BD=,求AD的长.
类型四 以中点为背景的旋转
8.(1)如图(a),在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;
②若∠A=90°,探索线段BE,CF,EF之间的数量关系,并加以证明.
(2)如图(b),在四边形ABDC中,∠B+∠C=180°,BD=CD,∠BDC=120°,以D为顶点作一个60°的角,角的两边分别交AB,AC于E,F两点,连接EF,探索线段BE,CF,EF之间的数量关系,并加以证明.
答案
1.A 点P(-4,2)向右平移7个单位长度得到点P1(3,2),点P1绕原点逆时针旋转90°得到点P2(-2,3).故选A.
2.C
如图,过点A作AE⊥OB于点E,过点A′作A′H⊥x轴于点H.
∵B(2,0),△OAB是等边三角形,
∴OA=OB=AB=2.
∵AE⊥OB,
∴OE=EB=1,
∴AE===.
∵以点O为旋转中心把△OAB逆时针旋转90°,旋转后点A的对应点为A′,A′H⊥OH,
∴∠A′HO=∠OEA=∠AOA′=90°,OA′=OA,
∴∠A′OH+∠AOE=90°,∠AOE+∠OAE=90°,
∴∠A′OH=∠OAE,
∴△A′OH≌△OAE(AAS),
∴A′H=OE=1,OH=AE=,
∴A′(-,1).
故选C.
3.90° 找到一组对应点A,A′,并将其与旋转中心连接起来,确定旋转角,进而得到旋转角的度数为90°.
4.(4,) 在y=x+4中,令x=0,得y=4;
令y=0,得0=x+4,解得x=-,
∴A(-,0),B(0,4).
由旋转可得△AOB≌△A1O1B,∠ABA1=90°,
∴∠ABO=∠A1BO1,∠BO1A1=∠BOA=90°,O1A1=OA=,O1B=OB=4,
∴∠OBO1=90°,
∴O1B∥x轴,
∴点A1的纵坐标为OB-O1A1的长,
即4-=,
横坐标为O1B=4,
故点A1的坐标是(4,).
5.解:将△BPC绕点B逆时针旋转60°得到△BP′A(如图).
连接PP′,由旋转的性质知△BPP′为等边三角形,∠BP′A=∠BPC,AP′=PC=1,
∴PP′=PB=,∠BPP′=∠BP′P=60°.
在△APP′中,∵AP′2+PP′2=12+()2=22=PA2,
∴△APP′是直角三角形,且∠AP′P=90°,
∴∠BP′A=∠BP′P+∠AP′P=60°+90°=150°,
∴∠BPC=∠BP′A=150°.
在Rt△APP′中,∵PA=2,AP′=1,
∴∠APP′=30°.
又∵∠BPP′=60°,∴∠APB=90°,
∴在Rt△ABP中,AB===,
即等边三角形ABC的边长为.
6.解:(1)①当A,D,M三点在同一直线上时,AM=AD+DM=40或AM=AD-DM=20.
②当A,D,M三点为同一直角三角形的顶点时,显然∠MAD不能为直角.
当∠AMD为直角时,AM2=AD2-DM2=302-102=800.
∵AM>0,
∴AM=20 .
当∠ADM=90°时,AM2=AD2+DM2=302+102=1000.
∵AM>0,
∴AM=10 .
综上所述,满足条件的AM的长为20 或10 .
(2)如图,连接CD1.
由题意,得∠D1AD2=90°,AD1=AD2=30,
∴∠AD2D1=45°,D1D2=30 .
∵∠AD2C=135°,
∴∠CD2D1=∠AD2C-∠AD2D1=90°,
∴CD1==30 .
∵∠BAC=∠D1AD2=90°,
∴∠BAC-∠CAD2=∠D1AD2-∠CAD2,
即∠BAD2=∠CAD1.
又∵AB=AC,AD2=AD1,
∴△BAD2≌△CAD1(SAS),
∴BD2=CD1=30 .
7.解:【问题初探】
(1)60° 如图①,延长DC交AB于点F,交BO于点E.
∵α=60°,
∴∠BOD=60°.
∵线段AB绕点O顺时针旋转得到线段CD,
∴AB=CD,OA=OC,BO=DO,
∴△AOB≌△COD(SSS),
∴∠B=∠D.
又∵∠OED=∠BEF,
∴∠BFE=∠EOD=60°.
(2)直线AB与直线CD所夹锐角与旋转角α互补.
理由如图下:
如图②,延长AB,DC交于点E.
∵线段AB绕点O顺时针旋转得到线段CD,
∴AB=CD,OA=OC,BO=DO,
∴△AOB≌△COD(SSS),
∴∠ABO=∠D.
∵∠ABO+∠EBO=180°,
∴∠D+∠EBO=180°.
又∵∠EBO+∠E+∠D+∠BOD=360°,
∴∠E+∠BOD=180°,
∴直线AB与直线CD所夹锐角与旋转角α互补.
【形成结论】相等或互补
【运用拓广】如图③,将△BCD绕点B顺时针旋转60°,得到△BAF,连接FD,延长FA,DC交于点E.
∵旋转角∠ABC=60°,
∴由【形成结论】可知∠AED=∠ABC=60°.
由旋转的性质可知AF=CD=3,BD=BF.
∵∠ADC=30°,
∴∠FAD=∠AED+∠ADC=90°.
∵∠FBD=∠ABC=60°,BF=BD,
∴△BFD是等边三角形,
∴DF=BF=BD=,
∴在Rt△DAF中,AD===.
8.解:(1)①证明:如图(a),将△DBE绕点D旋转180°得到△DCG,连接FG,则△DCG≌△DBE,
∴DG=DE,CG=BE.
又∵DE⊥DF,
∴DF垂直平分线段EG,∴FG=EF.
∵在△CFG中,CG+CF>FG,
∴BE+CF>EF.
②BE2+CF2=EF2.
证明:∵∠A=90°,∴∠B+∠ACD=90°.
由①可得,∠FCG=∠FCD+∠DCG=∠FCD+∠B=90°,
∴在Rt△CFG中,由勾股定理,得CG2+CF2=FG2,∴BE2+CF2=EF2.
(2)EF=BE+CF.
证明:如图(b).∵CD=BD,∠BDC=120°,
∴将△CDF绕点D逆时针旋转120°可得到△BDM,
∴△BDM≌△CDF,
∴DM=DF,BM=CF,∠BDM=∠CDF,∠DBM=∠C.
∵∠ABD+∠C=180°,
∴∠ABD+∠DBM=180°,
∴点A,B,M共线,
∴∠EDM=∠EDB+∠BDM=∠EDB+∠CDF=∠BDC-∠EDF=120°-60°=60°=∠EDF.
在△DEM和△DEF中,
∴△DEM≌△DEF,
∴EF=EM=BE+BM=BE+CF.
同课章节目录
