人教版数学九年级上册课课练:24.1.2垂直于弦的直径(Word版含答案)
文档属性
| 名称 | 人教版数学九年级上册课课练:24.1.2垂直于弦的直径(Word版含答案) | 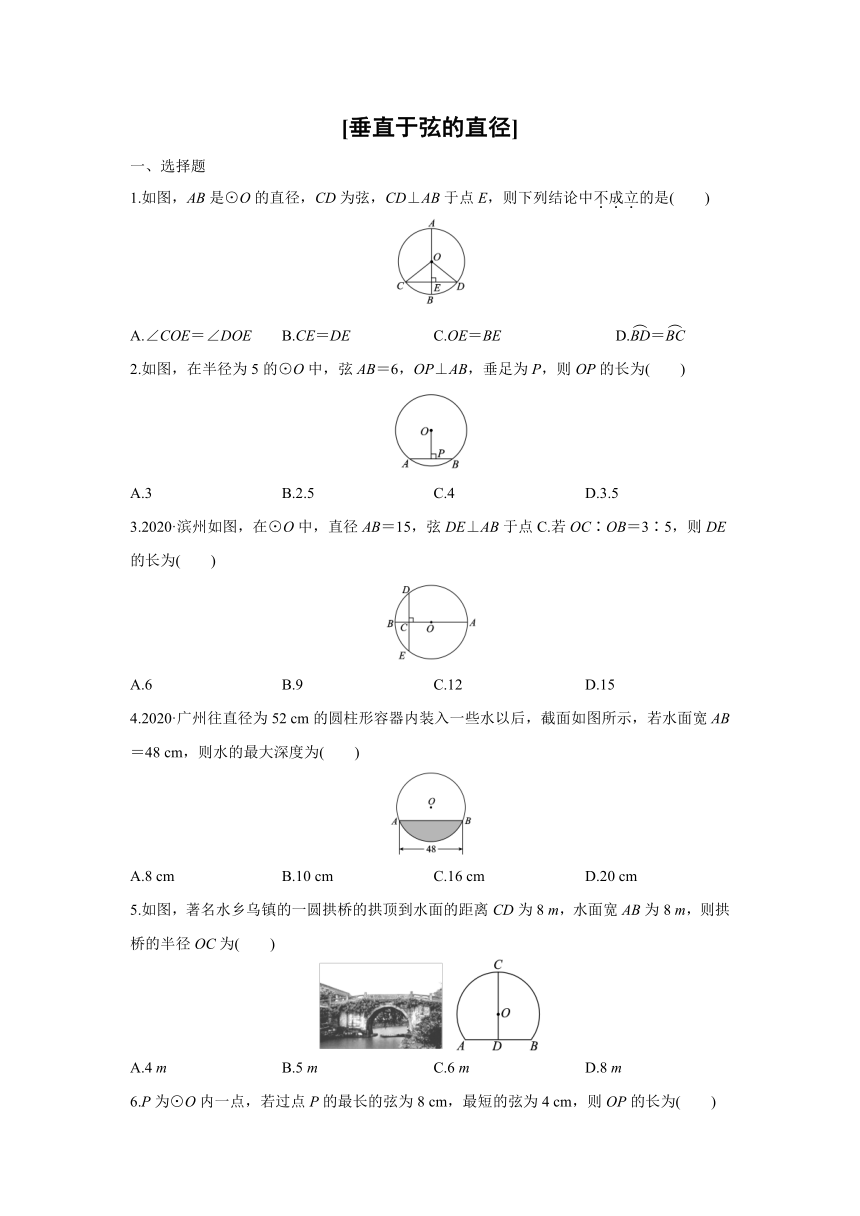 | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 09:30:39 | ||
图片预览


文档简介
[垂直于弦的直径]
一、选择题
1.如图,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是( )
A.∠COE=∠DOE B.CE=DE C.OE=BE D.=
2.如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为P,则OP的长为( )
A.3 B.2.5 C.4 D.3.5
3.2020·滨州如图,在⊙O中,直径AB=15,弦DE⊥AB于点C.若OC∶OB=3∶5,则DE的长为( )
A.6 B.9 C.12 D.15
4.2020·广州往直径为52 cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48 cm,则水的最大深度为( )
A.8 cm B.10 cm C.16 cm D.20 cm
5.如图,著名水乡乌镇的一圆拱桥的拱顶到水面的距离CD为8 m,水面宽AB为8 m,则拱桥的半径OC为( )
A.4 m B.5 m C.6 m D.8 m
6.P为⊙O内一点,若过点P的最长的弦为8 cm,最短的弦为4 cm,则OP的长为( )
A.2 cm B. cm C.3 cm D.2 cm
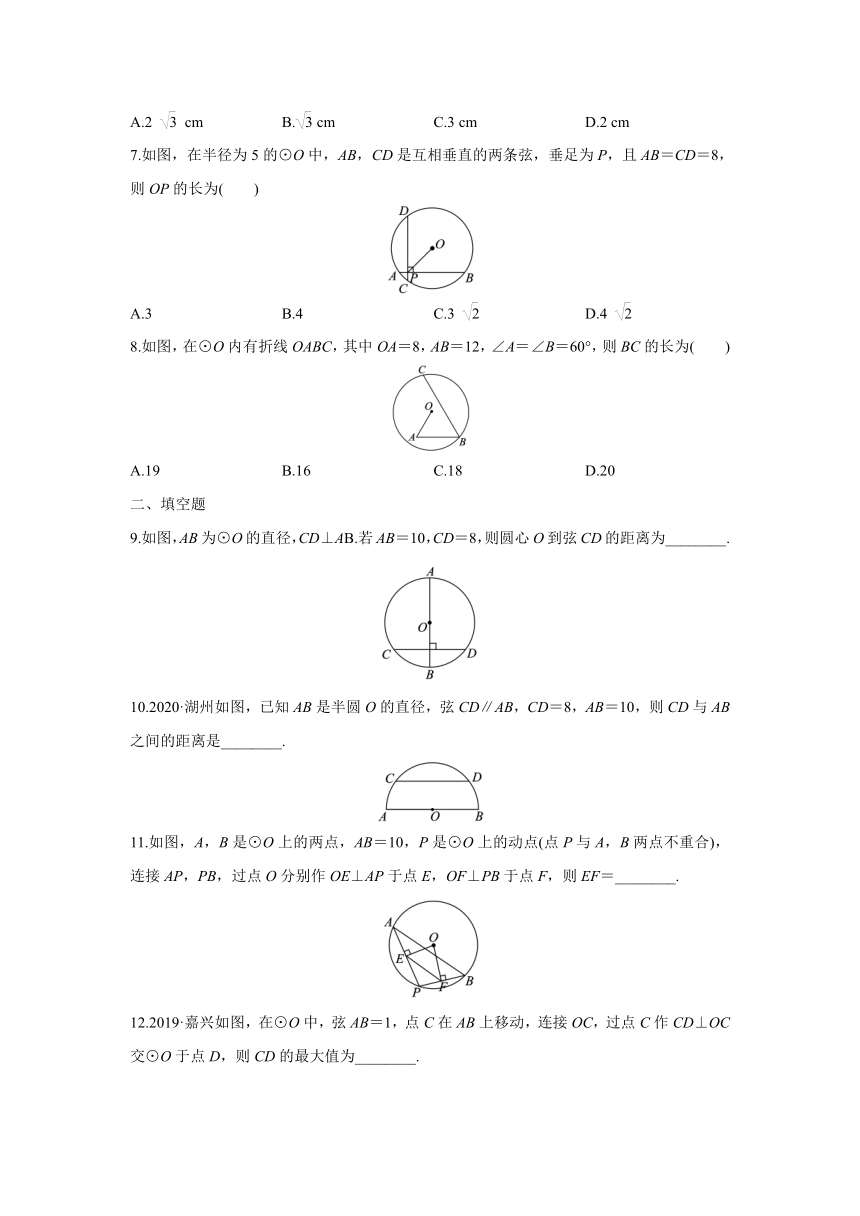
7.如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
A.3 B.4 C.3 D.4
8.如图,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
A.19 B.16 C.18 D.20
二、填空题
9.如图,AB为⊙O的直径,CD⊥AB.若AB=10,CD=8,则圆心O到弦CD的距离为________.
10.2020·湖州如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是________.
11.如图,A,B是⊙O上的两点,AB=10,P是⊙O上的动点(点P与A,B两点不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=________.
12.2019·嘉兴如图,在⊙O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为________.
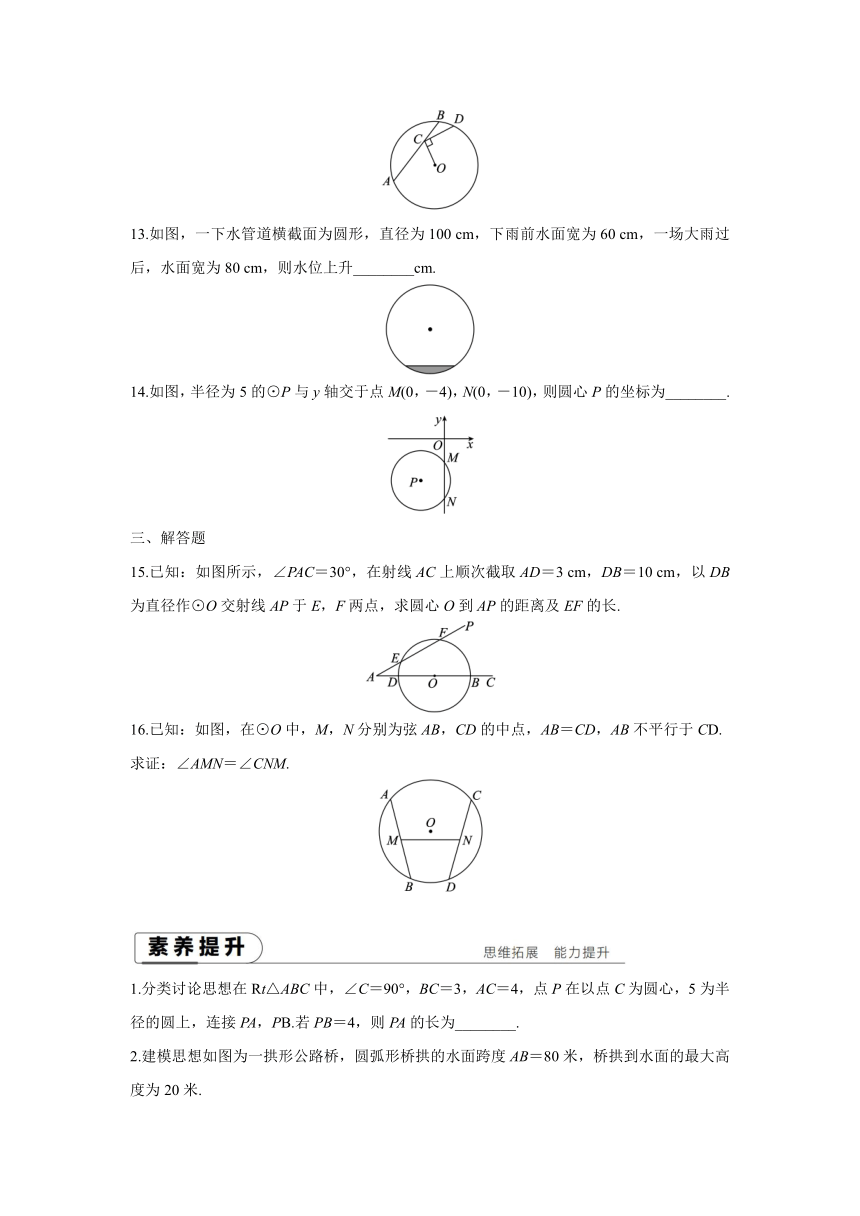
13.如图,一下水管道横截面为圆形,直径为100 cm,下雨前水面宽为60 cm,一场大雨过后,水面宽为80 cm,则水位上升________cm.
14.如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),则圆心P的坐标为________.
三、解答题
15.已知:如图所示,∠PAC=30°,在射线AC上顺次截取AD=3 cm,DB=10 cm,以DB为直径作⊙O交射线AP于E,F两点,求圆心O到AP的距离及EF的长.
16.已知:如图,在⊙O中,M,N分别为弦AB,CD的中点,AB=CD,AB不平行于CD.
求证:∠AMN=∠CNM.
1.分类讨论思想在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以点C为圆心,5为半径的圆上,连接PA,PB.若PB=4,则PA的长为________.
2.建模思想如图为一拱形公路桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.
(1)求桥拱的半径;
(2)现有一艘宽60米,船舱顶部为矩形并高出水面9米的轮船要经过这里,这艘轮船能顺利通过这座拱桥吗?请说明理由.
答案
1.C 2.C 3.C
4.C 如图,过点O作OC⊥AB于点D,交⊙O于点C,连接OA.
由题意,得OA=OC=26 cm,AD=AB=24 cm.
在Rt△AOD中,由勾股定理可得OD=10 cm,
所以水深CD=OC-OD=26-10=16(cm).
因此本题选C.
5.B 如图,连接OB.
由题意可得AD=BD=4 m.
设⊙O的半径OC=OB=x m,
则OD=(8-x)m.
在Rt△BOD中,由勾股定理,得x2=(8-x)2+42,解得x=5.
故拱桥的半径OC为5 m.
6.A 设⊙O中过点P的最长的弦为AB,最短的弦为CD,如图所示,则CD⊥AB于点P.
根据题意,得AB=8 cm,CD=4 cm,
∴OC=AB=4 cm.
∵CD⊥AB,∴CP=CD=2 cm.
在Rt△OCP中,根据勾股定理,得
OP===2 (cm).
7.C 如图,过点O作OE⊥AB,OF⊥CD,垂足分别为E,F,连接AO.
∵OE⊥AB,∴AE=AB=4.在Rt△OAE中,OA=5,由勾股定理可得OE=3,同理得OF=3.又∵AB⊥CD,∴四边形OEPF是正方形,∴PE=OE=3.在Rt△OPE中,由勾股定理可得OP=3 .
8.D 如图,延长AO交BC于点D,过点O作OE⊥BC于点E.
∵∠A=∠B=60°,∴△DAB是等边三角形,∴AD=DB=AB=12,∠ADB=∠A=60°,
∴OD=AD-OA=12-8=4.在Rt△ODE中,∵∠DOE=90°-∠ADB=30°,∴DE=OD=2,∴BE=DB-DE=12-2=10.由垂径定理,知BC=2BE=20.
9.3
10.3 过点O作OH⊥CD于点H,连接OC,如图,
则CH=DH=CD=4,OC=AB=5.
在Rt△OCH中,OH===3,
所以CD与AB之间的距离是3.
11.5 ∵OE过圆心且与AP垂直,
∴PE=EA.
同理PF=FB,∴EF是△PAB的中位线,
∴EF=AB=5.
12. 连接OD.因为CD⊥OC,所以CD=,根据题意可知圆的半径一定,故当OC最小时CD最大,故当OC⊥AB时CD最大,此时CD=AB=.
13.10或70 对于半径为50 cm的圆而言,圆心到长为60 cm的弦的距离为40 cm,到长为80 cm的弦的距离为30 cm.①当圆心在两平行弦之外时,两弦间的距离=40-30=10(cm);②当圆心在两平行弦之间时,两弦间的距离=40+30=70(cm).综上所述,水位上升10 cm或70 cm.
14.(-4,-7) 过点P作PH⊥MN于点H,连接PM,则MH=MN=3,OH=OM+MH=7.由勾股定理,得PH=4,∴圆心P的坐标为(-4,-7).
15.解: 如图,过点O作OG⊥AP于点G,连接OF.
∵DB=10 cm,
∴OD=OF=5 cm,
∴AO=AD+OD=3+5=8(cm).
∵∠PAC=30°,
∴OG=AO=×8=4(cm).
∵OG⊥EF,∴EG=GF=EF.
∵GF===3(cm),
∴EF=2GF=6 cm,
∴圆心O到AP的距离为4 cm,EF的长为6 cm.
16.证明:连接OM,ON,OA,OC,如图所示.
∵M,N分别为AB,CD的中点,
∴OM⊥AB,ON⊥CD,AM=AB,CN=CD,
∴∠AMO=∠CNO=90°.
又∵AB=CD,∴AM=CN.
在Rt△AOM和Rt△CON中,
∴Rt△AOM≌Rt△CON(HL),
∴OM=ON,
∴∠OMN=∠ONM,
∴∠AMO+∠OMN=∠CNO+∠ONM,
即∠AMN=∠CNM.
[素养提升]
1.3或 如图,连接CP,PB的延长线交⊙C于点P′.
∵PC=5,BC=3,PB=4,
∴BC2+PB2=PC2,
∴△CPB为直角三角形,且∠CBP=90°,
即CB⊥PB,∴PB=P′B=4.
∵∠ACB=90°,∴PB∥AC.
又∵PB=AC=4,
∴四边形ACBP为平行四边形.
又∵∠ACB=90°,∴ ACBP为矩形,
∴PA=BC=3.
在Rt△APP′中,∵PA=3,PP′=2BP=8,
∴P′A==.
综上所述,PA的长为3或.
2.解:(1)如图①,设点E是桥拱所在圆的圆心,连接AE,过点E作EF⊥AB于点F,延长EF交于点D.
根据垂径定理知F是AB的中点,D是的中点,DF的长是桥拱到水面的最大高度,
∴AF=FB=AB=40米,EF=DE-DF=AE-DF.
由勾股定理,知AE2=AF2+EF2=AF2+(AE-DF)2.
设桥拱的半径为r米,则r2=402+(r-20)2,
解得r=50.
答:桥拱的半径为50米.
(2)这艘轮船能顺利通过这座拱桥.理由如图下:
如图②,由题意,知MN∥AB.又∵DE⊥AB,∴DE⊥MN,则PM=MN=30米.
由(1)知,EF=50-20=30(米).
在Rt△PEM中,PE==40米,
∴PF=PE-EF=40-30=10(米).
∵10米>9米,
∴这艘轮船能顺利通过这座拱桥.
一、选择题
1.如图,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是( )
A.∠COE=∠DOE B.CE=DE C.OE=BE D.=
2.如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为P,则OP的长为( )
A.3 B.2.5 C.4 D.3.5
3.2020·滨州如图,在⊙O中,直径AB=15,弦DE⊥AB于点C.若OC∶OB=3∶5,则DE的长为( )
A.6 B.9 C.12 D.15
4.2020·广州往直径为52 cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48 cm,则水的最大深度为( )
A.8 cm B.10 cm C.16 cm D.20 cm
5.如图,著名水乡乌镇的一圆拱桥的拱顶到水面的距离CD为8 m,水面宽AB为8 m,则拱桥的半径OC为( )
A.4 m B.5 m C.6 m D.8 m
6.P为⊙O内一点,若过点P的最长的弦为8 cm,最短的弦为4 cm,则OP的长为( )
A.2 cm B. cm C.3 cm D.2 cm
7.如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
A.3 B.4 C.3 D.4
8.如图,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
A.19 B.16 C.18 D.20
二、填空题
9.如图,AB为⊙O的直径,CD⊥AB.若AB=10,CD=8,则圆心O到弦CD的距离为________.
10.2020·湖州如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是________.
11.如图,A,B是⊙O上的两点,AB=10,P是⊙O上的动点(点P与A,B两点不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF=________.
12.2019·嘉兴如图,在⊙O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为________.
13.如图,一下水管道横截面为圆形,直径为100 cm,下雨前水面宽为60 cm,一场大雨过后,水面宽为80 cm,则水位上升________cm.
14.如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),则圆心P的坐标为________.
三、解答题
15.已知:如图所示,∠PAC=30°,在射线AC上顺次截取AD=3 cm,DB=10 cm,以DB为直径作⊙O交射线AP于E,F两点,求圆心O到AP的距离及EF的长.
16.已知:如图,在⊙O中,M,N分别为弦AB,CD的中点,AB=CD,AB不平行于CD.
求证:∠AMN=∠CNM.
1.分类讨论思想在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以点C为圆心,5为半径的圆上,连接PA,PB.若PB=4,则PA的长为________.
2.建模思想如图为一拱形公路桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.
(1)求桥拱的半径;
(2)现有一艘宽60米,船舱顶部为矩形并高出水面9米的轮船要经过这里,这艘轮船能顺利通过这座拱桥吗?请说明理由.
答案
1.C 2.C 3.C
4.C 如图,过点O作OC⊥AB于点D,交⊙O于点C,连接OA.
由题意,得OA=OC=26 cm,AD=AB=24 cm.
在Rt△AOD中,由勾股定理可得OD=10 cm,
所以水深CD=OC-OD=26-10=16(cm).
因此本题选C.
5.B 如图,连接OB.
由题意可得AD=BD=4 m.
设⊙O的半径OC=OB=x m,
则OD=(8-x)m.
在Rt△BOD中,由勾股定理,得x2=(8-x)2+42,解得x=5.
故拱桥的半径OC为5 m.
6.A 设⊙O中过点P的最长的弦为AB,最短的弦为CD,如图所示,则CD⊥AB于点P.
根据题意,得AB=8 cm,CD=4 cm,
∴OC=AB=4 cm.
∵CD⊥AB,∴CP=CD=2 cm.
在Rt△OCP中,根据勾股定理,得
OP===2 (cm).
7.C 如图,过点O作OE⊥AB,OF⊥CD,垂足分别为E,F,连接AO.
∵OE⊥AB,∴AE=AB=4.在Rt△OAE中,OA=5,由勾股定理可得OE=3,同理得OF=3.又∵AB⊥CD,∴四边形OEPF是正方形,∴PE=OE=3.在Rt△OPE中,由勾股定理可得OP=3 .
8.D 如图,延长AO交BC于点D,过点O作OE⊥BC于点E.
∵∠A=∠B=60°,∴△DAB是等边三角形,∴AD=DB=AB=12,∠ADB=∠A=60°,
∴OD=AD-OA=12-8=4.在Rt△ODE中,∵∠DOE=90°-∠ADB=30°,∴DE=OD=2,∴BE=DB-DE=12-2=10.由垂径定理,知BC=2BE=20.
9.3
10.3 过点O作OH⊥CD于点H,连接OC,如图,
则CH=DH=CD=4,OC=AB=5.
在Rt△OCH中,OH===3,
所以CD与AB之间的距离是3.
11.5 ∵OE过圆心且与AP垂直,
∴PE=EA.
同理PF=FB,∴EF是△PAB的中位线,
∴EF=AB=5.
12. 连接OD.因为CD⊥OC,所以CD=,根据题意可知圆的半径一定,故当OC最小时CD最大,故当OC⊥AB时CD最大,此时CD=AB=.
13.10或70 对于半径为50 cm的圆而言,圆心到长为60 cm的弦的距离为40 cm,到长为80 cm的弦的距离为30 cm.①当圆心在两平行弦之外时,两弦间的距离=40-30=10(cm);②当圆心在两平行弦之间时,两弦间的距离=40+30=70(cm).综上所述,水位上升10 cm或70 cm.
14.(-4,-7) 过点P作PH⊥MN于点H,连接PM,则MH=MN=3,OH=OM+MH=7.由勾股定理,得PH=4,∴圆心P的坐标为(-4,-7).
15.解: 如图,过点O作OG⊥AP于点G,连接OF.
∵DB=10 cm,
∴OD=OF=5 cm,
∴AO=AD+OD=3+5=8(cm).
∵∠PAC=30°,
∴OG=AO=×8=4(cm).
∵OG⊥EF,∴EG=GF=EF.
∵GF===3(cm),
∴EF=2GF=6 cm,
∴圆心O到AP的距离为4 cm,EF的长为6 cm.
16.证明:连接OM,ON,OA,OC,如图所示.
∵M,N分别为AB,CD的中点,
∴OM⊥AB,ON⊥CD,AM=AB,CN=CD,
∴∠AMO=∠CNO=90°.
又∵AB=CD,∴AM=CN.
在Rt△AOM和Rt△CON中,
∴Rt△AOM≌Rt△CON(HL),
∴OM=ON,
∴∠OMN=∠ONM,
∴∠AMO+∠OMN=∠CNO+∠ONM,
即∠AMN=∠CNM.
[素养提升]
1.3或 如图,连接CP,PB的延长线交⊙C于点P′.
∵PC=5,BC=3,PB=4,
∴BC2+PB2=PC2,
∴△CPB为直角三角形,且∠CBP=90°,
即CB⊥PB,∴PB=P′B=4.
∵∠ACB=90°,∴PB∥AC.
又∵PB=AC=4,
∴四边形ACBP为平行四边形.
又∵∠ACB=90°,∴ ACBP为矩形,
∴PA=BC=3.
在Rt△APP′中,∵PA=3,PP′=2BP=8,
∴P′A==.
综上所述,PA的长为3或.
2.解:(1)如图①,设点E是桥拱所在圆的圆心,连接AE,过点E作EF⊥AB于点F,延长EF交于点D.
根据垂径定理知F是AB的中点,D是的中点,DF的长是桥拱到水面的最大高度,
∴AF=FB=AB=40米,EF=DE-DF=AE-DF.
由勾股定理,知AE2=AF2+EF2=AF2+(AE-DF)2.
设桥拱的半径为r米,则r2=402+(r-20)2,
解得r=50.
答:桥拱的半径为50米.
(2)这艘轮船能顺利通过这座拱桥.理由如图下:
如图②,由题意,知MN∥AB.又∵DE⊥AB,∴DE⊥MN,则PM=MN=30米.
由(1)知,EF=50-20=30(米).
在Rt△PEM中,PE==40米,
∴PF=PE-EF=40-30=10(米).
∵10米>9米,
∴这艘轮船能顺利通过这座拱桥.
同课章节目录
