人教版数学九年级上册课课练:23章 旋转 单元复习训练(含答案解析)
文档属性
| 名称 | 人教版数学九年级上册课课练:23章 旋转 单元复习训练(含答案解析) | 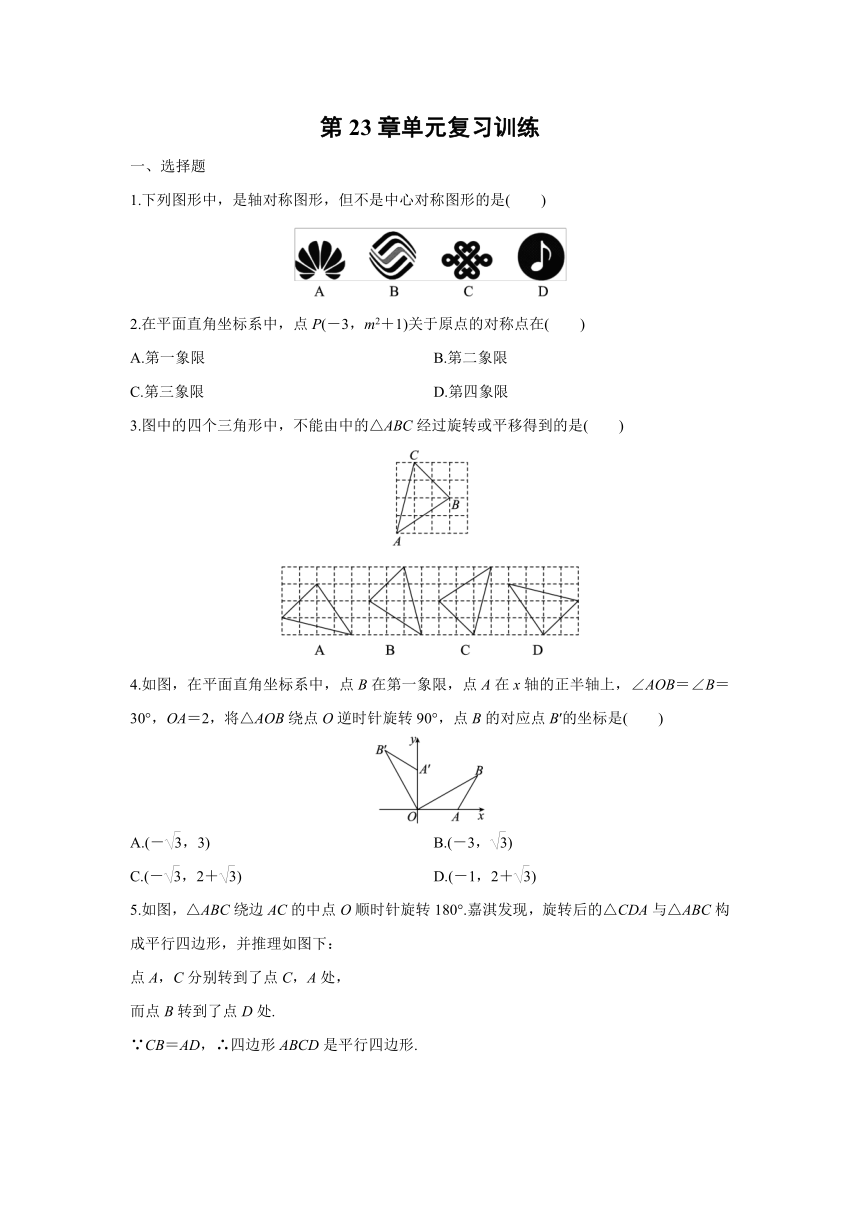 | |
| 格式 | docx | ||
| 文件大小 | 732.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 15:14:26 | ||
图片预览



文档简介
第23章单元复习训练
一、选择题
1.下列图形中,是轴对称图形,但不是中心对称图形的是( )
2.在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.图中的四个三角形中,不能由中的△ABC经过旋转或平移得到的是( )
4.如图,在平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是( )
A.(-,3) B.(-3,)
C.(-,2+) D.(-1,2+)
5.如图,△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC构成平行四边形,并推理如图下:
点A,C分别转到了点C,A处,
而点B转到了点D处.
∵CB=AD,∴四边形ABCD是平行四边形.
小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形……”之间作补充.下列正确的是( )
A.嘉淇推理严谨,不必补充
B.应补充:AB=CD,
C.应补充:且AB∥CD,
D.应补充:且OA=OC,
6.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′,使点C′落在AB边上,连接BB′,则BB′的长度是( )
A.1 cm B.2 cm C. cm D.2 cm
二、填空题
7.如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为________.
8.如图,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE,直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF,连接EF,若AB=3,AC=2,且α+β=∠B,则EF=________.
9.如图,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为A(0,3),B(-1,1),C(3,1).△A′B′C′是△ABC关于x轴的对称图形,将△A′B′C′绕点B′逆时针旋转180°,点A′的对应点为M,则点M的坐标为________.
三、解答题
10.①②都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
(1)使得4个阴影小等边三角形组成一个轴对称图形;
(2)使得4个阴影小等边三角形组成一个中心对称图形.
(请将两个小题依次作答在图①,图②中,均只需画出符合条件的一种情形)
11.如图①,等腰直角三角形OEF的直角顶点O为正方形ABCD的中心,点C,D分别在OE和OF上,现将△OEF绕点O逆时针旋转角α(0°<α<90°),连接AF,DE(如图②).
(1)在图②中,∠AOF=________;(用含α的式子表示)
(2)猜想图②中AF与DE的数量关系,并证明你的结论.
12.节选背景:一次小组合作探究课上,小明将两个正方形按如图所示的位置摆放(点E,A,D在同一条直线上),发现BE=DG且BE⊥DG.
小组讨论后,提出了下列两个问题,请你帮助解答:
(1)将正方形AEFG绕点A按逆时针方向旋转(如图①),还能得到BE=DG吗?若能,请给出证明;若不能,请说明理由.
(2)把背景中的正方形AEFG和正方形ABCD分别改成菱形AEFG和菱形ABCD,将菱形AEFG绕点A按逆时针方向旋转(如图②),当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由.
答案
1.A
2.D
3.B
4.A 如图,过点B′作B′H⊥y轴于点H.
∵∠AOB=∠B=30°,
∴AB=OA=2,∠OAB=120°.
由旋转知点A′在y轴的正半轴上,OA′=OA=2,A′B′=AB=2,∠OA′B′=∠OAB=120°,
∴∠B′A′H=60°,∴∠A′B′H=30°,
∴A′H=A′B′=1,B′H=,
∴OH=2+1=3,∴点B′的坐标是(-,3).
5.B 因为“一组对边相等的四边形不一定是平行四边形”,所以“∵CB=AD,∴四边形ABCD是平行四边形”的推理不严谨;补充“AB=CD,”,根据“两组对边相等的四边形是平行四边形”可知补充后推理正确,故选项B正确.
6.B 在Rt△ABC中,∠ABC=30°,则AB=2AC=2 cm,且∠BAC=60°.由旋转的性质,得AB=AB′,∠B′AC′=∠BAC=60°,
∴△ABB′是等边三角形,故BB′=AB=2 cm.
7.(4,2) 如图所示,连接AC,BD,分别作AC,BD的垂直平分线交于点P,则点P即为旋转中心,P(4,2).
8. ∵α+β=∠B,∴∠EAF=∠BAC+∠B=90°,∴△AEF是直角三角形,且AE=AB=3,AF=AC=2,∴EF==.
9.(-2,1)
10.解:(1)画出下列其中一种即可.
(2)画出下列其中一种即可.
11.解:(1)90°-α ∵△OEF绕点O逆时针旋转角α,∴∠DOF=∠COE=α.
∵四边形ABCD为正方形,
∴∠AOD=90°,∴∠AOF=90°-α.
(2)猜想:AF=DE.
证明:∵四边形ABCD为正方形,
∴∠AOD=∠COD=90°,OA=OD.
∵∠DOF=∠COE=α,
∴∠AOF=∠DOE.
∵△OEF为等腰直角三角形,
∴OF=OE.
在△AOF和△DOE中,
∴△AOF≌△DOE(SAS),
∴AF=DE.
12.解:(1)能得到BE=DG.
证明:∵四边形AEFG是正方形,
∴AE=AG,∠EAG=90°.
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠EAG=∠BAD,
∴∠EAG-∠BAG=∠BAD-∠BAG,
即∠EAB=∠GAD,
∴△EAB≌△GAD(SAS),∴BE=DG.
(2)当∠EAG=∠BAD时,背景中的结论BE=DG仍成立.
理由如图下:∵∠EAG=∠BAD,
∴∠EAB=∠GAD.
∵四边形AEFG和四边形ABCD均为菱形,
∴AE=AG,AB=AD,
∴△AEB≌△AGD(SAS),
∴BE=DG.
一、选择题
1.下列图形中,是轴对称图形,但不是中心对称图形的是( )
2.在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.图中的四个三角形中,不能由中的△ABC经过旋转或平移得到的是( )
4.如图,在平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是( )
A.(-,3) B.(-3,)
C.(-,2+) D.(-1,2+)
5.如图,△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC构成平行四边形,并推理如图下:
点A,C分别转到了点C,A处,
而点B转到了点D处.
∵CB=AD,∴四边形ABCD是平行四边形.
小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形……”之间作补充.下列正确的是( )
A.嘉淇推理严谨,不必补充
B.应补充:AB=CD,
C.应补充:且AB∥CD,
D.应补充:且OA=OC,
6.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′,使点C′落在AB边上,连接BB′,则BB′的长度是( )
A.1 cm B.2 cm C. cm D.2 cm
二、填空题
7.如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为________.
8.如图,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE,直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF,连接EF,若AB=3,AC=2,且α+β=∠B,则EF=________.
9.如图,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为A(0,3),B(-1,1),C(3,1).△A′B′C′是△ABC关于x轴的对称图形,将△A′B′C′绕点B′逆时针旋转180°,点A′的对应点为M,则点M的坐标为________.
三、解答题
10.①②都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
(1)使得4个阴影小等边三角形组成一个轴对称图形;
(2)使得4个阴影小等边三角形组成一个中心对称图形.
(请将两个小题依次作答在图①,图②中,均只需画出符合条件的一种情形)
11.如图①,等腰直角三角形OEF的直角顶点O为正方形ABCD的中心,点C,D分别在OE和OF上,现将△OEF绕点O逆时针旋转角α(0°<α<90°),连接AF,DE(如图②).
(1)在图②中,∠AOF=________;(用含α的式子表示)
(2)猜想图②中AF与DE的数量关系,并证明你的结论.
12.节选背景:一次小组合作探究课上,小明将两个正方形按如图所示的位置摆放(点E,A,D在同一条直线上),发现BE=DG且BE⊥DG.
小组讨论后,提出了下列两个问题,请你帮助解答:
(1)将正方形AEFG绕点A按逆时针方向旋转(如图①),还能得到BE=DG吗?若能,请给出证明;若不能,请说明理由.
(2)把背景中的正方形AEFG和正方形ABCD分别改成菱形AEFG和菱形ABCD,将菱形AEFG绕点A按逆时针方向旋转(如图②),当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由.
答案
1.A
2.D
3.B
4.A 如图,过点B′作B′H⊥y轴于点H.
∵∠AOB=∠B=30°,
∴AB=OA=2,∠OAB=120°.
由旋转知点A′在y轴的正半轴上,OA′=OA=2,A′B′=AB=2,∠OA′B′=∠OAB=120°,
∴∠B′A′H=60°,∴∠A′B′H=30°,
∴A′H=A′B′=1,B′H=,
∴OH=2+1=3,∴点B′的坐标是(-,3).
5.B 因为“一组对边相等的四边形不一定是平行四边形”,所以“∵CB=AD,∴四边形ABCD是平行四边形”的推理不严谨;补充“AB=CD,”,根据“两组对边相等的四边形是平行四边形”可知补充后推理正确,故选项B正确.
6.B 在Rt△ABC中,∠ABC=30°,则AB=2AC=2 cm,且∠BAC=60°.由旋转的性质,得AB=AB′,∠B′AC′=∠BAC=60°,
∴△ABB′是等边三角形,故BB′=AB=2 cm.
7.(4,2) 如图所示,连接AC,BD,分别作AC,BD的垂直平分线交于点P,则点P即为旋转中心,P(4,2).
8. ∵α+β=∠B,∴∠EAF=∠BAC+∠B=90°,∴△AEF是直角三角形,且AE=AB=3,AF=AC=2,∴EF==.
9.(-2,1)
10.解:(1)画出下列其中一种即可.
(2)画出下列其中一种即可.
11.解:(1)90°-α ∵△OEF绕点O逆时针旋转角α,∴∠DOF=∠COE=α.
∵四边形ABCD为正方形,
∴∠AOD=90°,∴∠AOF=90°-α.
(2)猜想:AF=DE.
证明:∵四边形ABCD为正方形,
∴∠AOD=∠COD=90°,OA=OD.
∵∠DOF=∠COE=α,
∴∠AOF=∠DOE.
∵△OEF为等腰直角三角形,
∴OF=OE.
在△AOF和△DOE中,
∴△AOF≌△DOE(SAS),
∴AF=DE.
12.解:(1)能得到BE=DG.
证明:∵四边形AEFG是正方形,
∴AE=AG,∠EAG=90°.
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠EAG=∠BAD,
∴∠EAG-∠BAG=∠BAD-∠BAG,
即∠EAB=∠GAD,
∴△EAB≌△GAD(SAS),∴BE=DG.
(2)当∠EAG=∠BAD时,背景中的结论BE=DG仍成立.
理由如图下:∵∠EAG=∠BAD,
∴∠EAB=∠GAD.
∵四边形AEFG和四边形ABCD均为菱形,
∴AE=AG,AB=AD,
∴△AEB≌△AGD(SAS),
∴BE=DG.
同课章节目录
