全国人教版数学九年级上册课课练:24.1.1圆(含答案解析)
文档属性
| 名称 | 全国人教版数学九年级上册课课练:24.1.1圆(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 210.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 10:04:03 | ||
图片预览

文档简介
[圆]
一、选择题
1.下列说法中不正确的有( )
①过圆上一点可以作圆中最长的弦无数条;
②长度相等的弧是等弧;
③圆上的点到圆心的距离都相等;
④在同圆或等圆中,优弧一定比劣弧长.
A.1个 B.2个 C.3个 D.4个
2.M,N是⊙O上的两点,已知OM=3 cm,那么一定有( )
A.MN>6 cm B.MN=6 cm
C.0 cm3.有下列说法:①矩形的四个顶点在同一个圆上;②菱形的四个顶点在同一个圆上;③平行四边形的四个顶点在同一个圆上.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
4.如图,AB是⊙O的直径,点C,D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
5.如图,在△ABC中,∠ACB=90°,∠A=40°,以点C为圆心,CB的长为半径的圆交AB于点D,连接CD,则∠ACD的度数为( )
A.10° B.15° C.20° D.25°
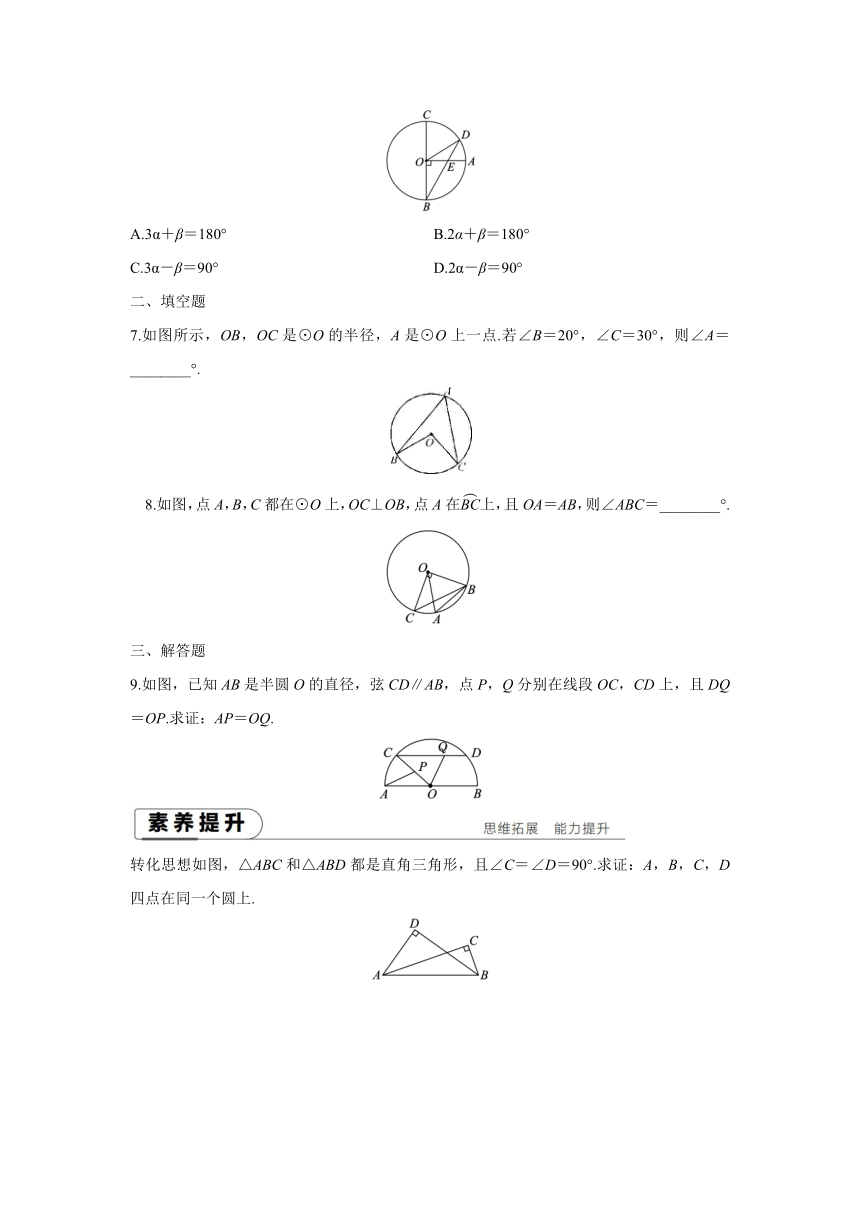
6.2020·杭州如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A.3α+β=180° B.2α+β=180°
C.3α-β=90° D.2α-β=90°
二、填空题
7.如图所示,OB,OC是⊙O的半径,A是⊙O上一点.若∠B=20°,∠C=30°,则∠A=________°.
8.如图,点A,B,C都在⊙O上,OC⊥OB,点A在上,且OA=AB,则∠ABC=________°.
三、解答题
9.如图,已知AB是半圆O的直径,弦CD∥AB,点P,Q分别在线段OC,CD上,且DQ=OP.求证:AP=OQ.
转化思想如图,△ABC和△ABD都是直角三角形,且∠C=∠D=90°.求证:A,B,C,D四点在同一个圆上.
答案
1.B ①②不正确.
2.D ∵OM=3 cm,∴⊙O的半径为3 cm,∴⊙O的直径为6 cm,
即⊙O中最长的弦的长度为6 cm,
∴MN最长为6 cm,∴0 cm<MN≤6 cm.
3.B 矩形的两条对角线的交点到矩形的四个顶点的距离相等,故它的四个顶点在以对角线的交点为圆心、对角线长的一半为半径的圆上.
4.D ∵∠BOC=110°,∴∠AOC=70°.∵AD∥OC,∴∠A=∠AOC=70°.∵OA=OD,∴∠D=∠A=70°.在△OAD中,∠AOD=180°-(∠A+∠D)=40°.
5.A ∵∠ACB=90°,∠A=40°,
∴∠B=50°.
∵CD=CB,∴∠BDC=∠B=50°,
∴∠BCD=180°-2×50°=80°,
∴∠ACD=90°-80°=10°.
6.D 因为OA⊥BC,所以∠AOB=90°.
因为OB=OD,所以∠B=∠D.
在△OBD中,∠B+∠D+∠BOD=180°,
即2∠D+90°+β=180°,
所以2∠D+β=90°.
因为∠AED是△ODE的外角,
所以∠D=∠AED-∠AOD=α-β,
所以2(α-β)+β=90°,
整理,得2α-β=90°.故选D.
7.50 连接OA,则OA=OB,OA=OC,
∴∠OAB=∠B,∠OAC=∠C,
∴∠BAC=∠OAB+∠OAC=∠B+∠C=20°+30°=50°.
8.15 ∵OC⊥OB,∴∠COB=90°.
又∵OC=OB,∴△COB是等腰直角三角形,
∴∠OBC=45°.
∵OA=AB,OA=OB,∴OA=AB=OB,
∴△AOB是等边三角形,∴∠OBA=60°,
∴∠ABC=∠OBA-∠OBC=15°.
9.证明:连接OD.∵OC=OD,∴∠C=∠D.
∵CD∥AB,∴∠C=∠AOP,
∴∠D=∠AOP.
又∵OP=DQ,AO=OD,
∴△AOP≌△ODQ,
∴AP=OQ.
[素养提升]
证明:如图,取AB的中点O,连接OC,OD.
∵△ABC和△ABD都是直角三角形,且∠ACB=∠ADB=90°,
∴OC,OD分别为Rt△ABC和Rt△ABD斜边上的中线,
∴OC=OA=OB,OD=OA=OB,
∴OA=OB=OC=OD,
∴A,B,C,D四点在同一个圆上.
一、选择题
1.下列说法中不正确的有( )
①过圆上一点可以作圆中最长的弦无数条;
②长度相等的弧是等弧;
③圆上的点到圆心的距离都相等;
④在同圆或等圆中,优弧一定比劣弧长.
A.1个 B.2个 C.3个 D.4个
2.M,N是⊙O上的两点,已知OM=3 cm,那么一定有( )
A.MN>6 cm B.MN=6 cm
C.0 cm
A.0个 B.1个 C.2个 D.3个
4.如图,AB是⊙O的直径,点C,D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
5.如图,在△ABC中,∠ACB=90°,∠A=40°,以点C为圆心,CB的长为半径的圆交AB于点D,连接CD,则∠ACD的度数为( )
A.10° B.15° C.20° D.25°
6.2020·杭州如图,已知BC是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则( )
A.3α+β=180° B.2α+β=180°
C.3α-β=90° D.2α-β=90°
二、填空题
7.如图所示,OB,OC是⊙O的半径,A是⊙O上一点.若∠B=20°,∠C=30°,则∠A=________°.
8.如图,点A,B,C都在⊙O上,OC⊥OB,点A在上,且OA=AB,则∠ABC=________°.
三、解答题
9.如图,已知AB是半圆O的直径,弦CD∥AB,点P,Q分别在线段OC,CD上,且DQ=OP.求证:AP=OQ.
转化思想如图,△ABC和△ABD都是直角三角形,且∠C=∠D=90°.求证:A,B,C,D四点在同一个圆上.
答案
1.B ①②不正确.
2.D ∵OM=3 cm,∴⊙O的半径为3 cm,∴⊙O的直径为6 cm,
即⊙O中最长的弦的长度为6 cm,
∴MN最长为6 cm,∴0 cm<MN≤6 cm.
3.B 矩形的两条对角线的交点到矩形的四个顶点的距离相等,故它的四个顶点在以对角线的交点为圆心、对角线长的一半为半径的圆上.
4.D ∵∠BOC=110°,∴∠AOC=70°.∵AD∥OC,∴∠A=∠AOC=70°.∵OA=OD,∴∠D=∠A=70°.在△OAD中,∠AOD=180°-(∠A+∠D)=40°.
5.A ∵∠ACB=90°,∠A=40°,
∴∠B=50°.
∵CD=CB,∴∠BDC=∠B=50°,
∴∠BCD=180°-2×50°=80°,
∴∠ACD=90°-80°=10°.
6.D 因为OA⊥BC,所以∠AOB=90°.
因为OB=OD,所以∠B=∠D.
在△OBD中,∠B+∠D+∠BOD=180°,
即2∠D+90°+β=180°,
所以2∠D+β=90°.
因为∠AED是△ODE的外角,
所以∠D=∠AED-∠AOD=α-β,
所以2(α-β)+β=90°,
整理,得2α-β=90°.故选D.
7.50 连接OA,则OA=OB,OA=OC,
∴∠OAB=∠B,∠OAC=∠C,
∴∠BAC=∠OAB+∠OAC=∠B+∠C=20°+30°=50°.
8.15 ∵OC⊥OB,∴∠COB=90°.
又∵OC=OB,∴△COB是等腰直角三角形,
∴∠OBC=45°.
∵OA=AB,OA=OB,∴OA=AB=OB,
∴△AOB是等边三角形,∴∠OBA=60°,
∴∠ABC=∠OBA-∠OBC=15°.
9.证明:连接OD.∵OC=OD,∴∠C=∠D.
∵CD∥AB,∴∠C=∠AOP,
∴∠D=∠AOP.
又∵OP=DQ,AO=OD,
∴△AOP≌△ODQ,
∴AP=OQ.
[素养提升]
证明:如图,取AB的中点O,连接OC,OD.
∵△ABC和△ABD都是直角三角形,且∠ACB=∠ADB=90°,
∴OC,OD分别为Rt△ABC和Rt△ABD斜边上的中线,
∴OC=OA=OB,OD=OA=OB,
∴OA=OB=OC=OD,
∴A,B,C,D四点在同一个圆上.
同课章节目录
