全国人教版数学九年级上册课课练:24.1.4圆周角(word、含答案 )
文档属性
| 名称 | 全国人教版数学九年级上册课课练:24.1.4圆周角(word、含答案 ) |

|
|
| 格式 | docx | ||
| 文件大小 | 784.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 00:00:00 | ||
图片预览


文档简介
[圆周角]
一、选择题
1.如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是( )
A.75° B.70° C.65° D.35°
2.2019·柳州如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是( )
A.∠B B.∠C C.∠DEB D.∠D
3.2020·淮安如图,点A,B,C在⊙O上,∠ACB=54°,则∠ABO的度数是( )
A.54° B.27° C.36° D.108°
4.2020·湖州如图,已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是( )
A.70° B.110° C.130° D.140°
5.2020·海南如图,已知AB是⊙O的直径,CD是弦,若∠BCD=36°,则∠ABD等于( )
A.54° B.56° C.64° D.66°
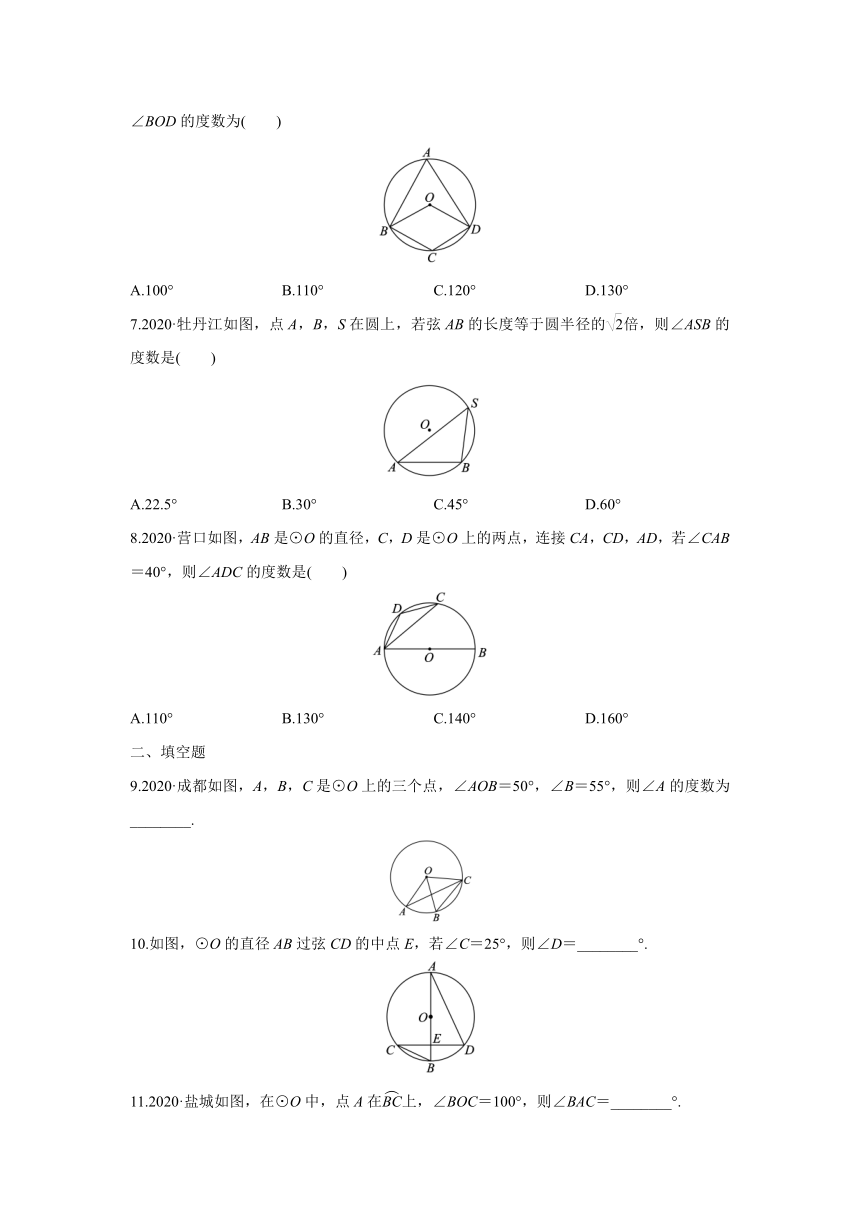
6.2020·张家界如图,四边形ABCD为⊙O的内接四边形,已知∠BCD的度数为120°,则∠BOD的度数为( )
A.100° B.110° C.120° D.130°
7.2020·牡丹江如图,点A,B,S在圆上,若弦AB的长度等于圆半径的倍,则∠ASB的度数是( )
A.22.5° B.30° C.45° D.60°
8.2020·营口如图,AB是⊙O的直径,C,D是⊙O上的两点,连接CA,CD,AD,若∠CAB=40°,则∠ADC的度数是( )
A.110° B.130° C.140° D.160°
二、填空题
9.2020·成都如图,A,B,C是⊙O上的三个点,∠AOB=50°,∠B=55°,则∠A的度数为________.
10.如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=________°.
11.2020·盐城如图,在⊙O中,点A在上,∠BOC=100°,则∠BAC=________°.
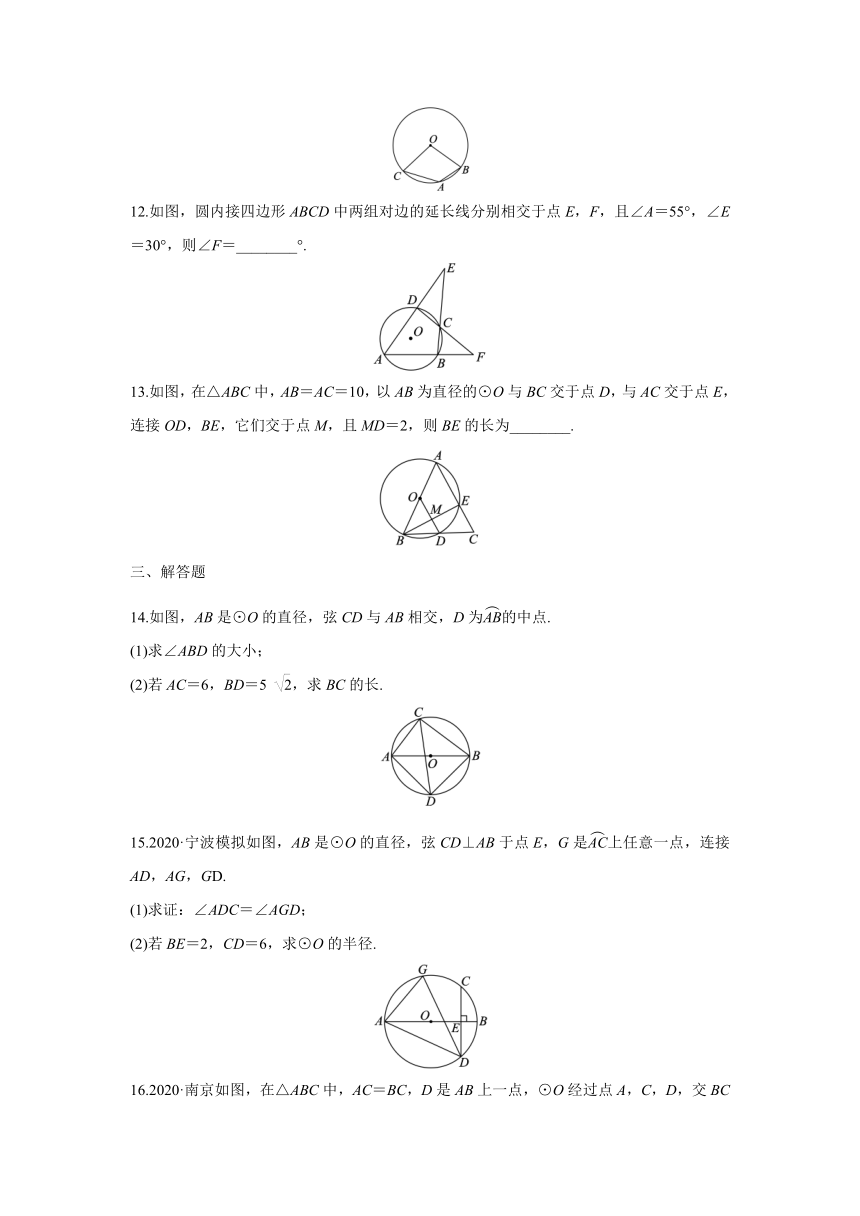
12.如图,圆内接四边形ABCD中两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=________°.
13.如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连接OD,BE,它们交于点M,且MD=2,则BE的长为________.
三、解答题
14.如图,AB是⊙O的直径,弦CD与AB相交,D为的中点.
(1)求∠ABD的大小;
(2)若AC=6,BD=5 ,求BC的长.
15.2020·宁波模拟如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上任意一点,连接AD,AG,GD.
(1)求证:∠ADC=∠AGD;
(2)若BE=2,CD=6,求⊙O的半径.
16.2020·南京如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A,C,D,交BC于点E,过点D作DF∥BC,交⊙O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
转化思想2019·包头如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=2 ,弦BM平分∠ABC交AC于点D,连接MA,MC.
(1)求⊙O的半径;
(2)求证:AB+BC=BM.
答案
1.B 2.D 3.C 4.B 5.A 6.C
7.C 设圆心为O,连接OA,OB,如图.
∵弦AB的长度等于圆半径的倍,即AB=OA=OB,
∴OA2+OB2=AB2,
∴△OAB为等腰直角三角形,∠AOB=90°.
根据圆周角定理可得∠ASB=∠AOB=45°.故选C.
8.B 如图,连接BC.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°.
∵∠CAB=40°,∴∠CBA=50°.
∵∠ADC+∠CBA=180°,∴∠ADC=130°.
9.30° ∵OB=OC,∠B=55°,∴∠BOC=180°-2∠B=70°.∵∠AOB=50°,∴∠AOC=∠AOB+∠BOC=70°+50°=120°.∵OA=OC,∴∠A=∠OCA==30°.
10.65 ∵∠C=25°,∴∠A=∠C=25°.
∵⊙O的直径AB过弦CD的中点E,
∴AB⊥CD,∴∠AED=90°,
∴∠D=90°-25°=65°.
11.130 如图,在⊙O上取一点D,连接CD,BD,
则∠BDC=∠BOC=50°.
∵四边形ABDC为圆内接四边形,
∴∠BAC+∠BDC=180°.
∵∠BDC=50°,
∴∠BAC=130°.
12.40 ∵∠BCD=180°-∠A=125°,∠CBF=∠A+∠E=85°,∴∠F=∠BCD-∠CBF=125°-85°=40°.
13.8 连接AD,如图所示.
∵以AB为直径的⊙O与BC交于点D,与AC交于点E,
∴∠AEB=∠ADB=90°,即AC⊥BE,AD⊥BC.
又∵AB=AC,
∴BD=CD.
又∵OA=OB,∴OD∥AC,
∴OD⊥BE,∴BM=EM,
∴CE=2MD=4,
∴AE=AC-CE=6,
∴BE===8.
14.解:(1)∵D为的中点,
∴=.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ABD=∠DAB=45°.
(2)由(1)知=,
∴AD=BD=5 .
又∵∠ADB=90°,
∴AB==10.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC===8.
15.解:(1)证明:∵AB⊥CD,AB是⊙O的直径,
∴=,
∴∠ADC=∠AGD.
(2)连接OC,如图.
∵AB⊥CD,AB是⊙O的直径,
∴CE=DE=CD=3,∠OEC=90°.
设OC=r,
∵BE=2,
∴OE=r-2.
在Rt△OEC中,32+(r-2)2=r2,
解得r=,
∴⊙O的半径为.
16.证明:(1)∵AC=BC,
∴∠BAC=∠B.
∵DF∥BC,
∴∠ADF=∠B.
又∵∠BAC=∠CFD,
∴∠ADF=∠CFD,
∴BD∥CF.
又∵DF∥BC,
∴四边形DBCF是平行四边形.
(2)如图,连接AE.
∵∠ADF=∠B,∠ADF=∠AEF,
∴∠AEF=∠B.
∵四边形AECF是⊙O的内接四边形,
∴∠ECF+∠EAF=180°.
∵BD∥CF,∴∠ECF+∠B=180°,
∴∠EAF=∠B,
∴∠AEF=∠EAF,∴AF=EF.
[素养提升]
解:(1)连接OA,OC,过点O作OH⊥AC于点H,如图①.
∵∠ABC=120°,
∴∠AMC=180°-∠ABC=60°,
∴∠AOC=2∠AMC=120°.
∵OH⊥AC,
∴AH=CH=AC=,∠AOH=∠AOC=60°,
∴∠OAH=30°,∴OH=OA.
在Rt△AOH中,由勾股定理,得OH2+AH2=OA2,即(OA)2+()2=OA2,
解得OA=2,
故⊙O的半径为2.
(2)证明:在BM上截取BE=BC,连接CE,如图②.
∵∠ABC=120°,BM平分∠ABC,
∴∠MBC=∠ABM=∠ABC=60°.
又∵BE=BC,
∴△EBC是等边三角形,
∴EC=BC=BE,∠BCE=60°,
∴∠BCD+∠DCE=60°.
∵∠ACM=∠ABM=60°,
∴∠ECM+∠DCE=60°,
∴∠ECM=∠BCD.
∵∠MAC=∠MBC=60°,∠AMC=60°,
∴∠MAC=∠AMC=∠ACM,
∴△ACM是等边三角形,∴AC=MC.
在△ACB和△MCE中,
∴△ACB≌△MCE,
∴AB=ME.
∵ME+BE=BM,
∴AB+BC=BM.
一、选择题
1.如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是( )
A.75° B.70° C.65° D.35°
2.2019·柳州如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是( )
A.∠B B.∠C C.∠DEB D.∠D
3.2020·淮安如图,点A,B,C在⊙O上,∠ACB=54°,则∠ABO的度数是( )
A.54° B.27° C.36° D.108°
4.2020·湖州如图,已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是( )
A.70° B.110° C.130° D.140°
5.2020·海南如图,已知AB是⊙O的直径,CD是弦,若∠BCD=36°,则∠ABD等于( )
A.54° B.56° C.64° D.66°
6.2020·张家界如图,四边形ABCD为⊙O的内接四边形,已知∠BCD的度数为120°,则∠BOD的度数为( )
A.100° B.110° C.120° D.130°
7.2020·牡丹江如图,点A,B,S在圆上,若弦AB的长度等于圆半径的倍,则∠ASB的度数是( )
A.22.5° B.30° C.45° D.60°
8.2020·营口如图,AB是⊙O的直径,C,D是⊙O上的两点,连接CA,CD,AD,若∠CAB=40°,则∠ADC的度数是( )
A.110° B.130° C.140° D.160°
二、填空题
9.2020·成都如图,A,B,C是⊙O上的三个点,∠AOB=50°,∠B=55°,则∠A的度数为________.
10.如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=________°.
11.2020·盐城如图,在⊙O中,点A在上,∠BOC=100°,则∠BAC=________°.
12.如图,圆内接四边形ABCD中两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=________°.
13.如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连接OD,BE,它们交于点M,且MD=2,则BE的长为________.
三、解答题
14.如图,AB是⊙O的直径,弦CD与AB相交,D为的中点.
(1)求∠ABD的大小;
(2)若AC=6,BD=5 ,求BC的长.
15.2020·宁波模拟如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上任意一点,连接AD,AG,GD.
(1)求证:∠ADC=∠AGD;
(2)若BE=2,CD=6,求⊙O的半径.
16.2020·南京如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A,C,D,交BC于点E,过点D作DF∥BC,交⊙O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
转化思想2019·包头如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC=2 ,弦BM平分∠ABC交AC于点D,连接MA,MC.
(1)求⊙O的半径;
(2)求证:AB+BC=BM.
答案
1.B 2.D 3.C 4.B 5.A 6.C
7.C 设圆心为O,连接OA,OB,如图.
∵弦AB的长度等于圆半径的倍,即AB=OA=OB,
∴OA2+OB2=AB2,
∴△OAB为等腰直角三角形,∠AOB=90°.
根据圆周角定理可得∠ASB=∠AOB=45°.故选C.
8.B 如图,连接BC.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°.
∵∠CAB=40°,∴∠CBA=50°.
∵∠ADC+∠CBA=180°,∴∠ADC=130°.
9.30° ∵OB=OC,∠B=55°,∴∠BOC=180°-2∠B=70°.∵∠AOB=50°,∴∠AOC=∠AOB+∠BOC=70°+50°=120°.∵OA=OC,∴∠A=∠OCA==30°.
10.65 ∵∠C=25°,∴∠A=∠C=25°.
∵⊙O的直径AB过弦CD的中点E,
∴AB⊥CD,∴∠AED=90°,
∴∠D=90°-25°=65°.
11.130 如图,在⊙O上取一点D,连接CD,BD,
则∠BDC=∠BOC=50°.
∵四边形ABDC为圆内接四边形,
∴∠BAC+∠BDC=180°.
∵∠BDC=50°,
∴∠BAC=130°.
12.40 ∵∠BCD=180°-∠A=125°,∠CBF=∠A+∠E=85°,∴∠F=∠BCD-∠CBF=125°-85°=40°.
13.8 连接AD,如图所示.
∵以AB为直径的⊙O与BC交于点D,与AC交于点E,
∴∠AEB=∠ADB=90°,即AC⊥BE,AD⊥BC.
又∵AB=AC,
∴BD=CD.
又∵OA=OB,∴OD∥AC,
∴OD⊥BE,∴BM=EM,
∴CE=2MD=4,
∴AE=AC-CE=6,
∴BE===8.
14.解:(1)∵D为的中点,
∴=.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ABD=∠DAB=45°.
(2)由(1)知=,
∴AD=BD=5 .
又∵∠ADB=90°,
∴AB==10.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC===8.
15.解:(1)证明:∵AB⊥CD,AB是⊙O的直径,
∴=,
∴∠ADC=∠AGD.
(2)连接OC,如图.
∵AB⊥CD,AB是⊙O的直径,
∴CE=DE=CD=3,∠OEC=90°.
设OC=r,
∵BE=2,
∴OE=r-2.
在Rt△OEC中,32+(r-2)2=r2,
解得r=,
∴⊙O的半径为.
16.证明:(1)∵AC=BC,
∴∠BAC=∠B.
∵DF∥BC,
∴∠ADF=∠B.
又∵∠BAC=∠CFD,
∴∠ADF=∠CFD,
∴BD∥CF.
又∵DF∥BC,
∴四边形DBCF是平行四边形.
(2)如图,连接AE.
∵∠ADF=∠B,∠ADF=∠AEF,
∴∠AEF=∠B.
∵四边形AECF是⊙O的内接四边形,
∴∠ECF+∠EAF=180°.
∵BD∥CF,∴∠ECF+∠B=180°,
∴∠EAF=∠B,
∴∠AEF=∠EAF,∴AF=EF.
[素养提升]
解:(1)连接OA,OC,过点O作OH⊥AC于点H,如图①.
∵∠ABC=120°,
∴∠AMC=180°-∠ABC=60°,
∴∠AOC=2∠AMC=120°.
∵OH⊥AC,
∴AH=CH=AC=,∠AOH=∠AOC=60°,
∴∠OAH=30°,∴OH=OA.
在Rt△AOH中,由勾股定理,得OH2+AH2=OA2,即(OA)2+()2=OA2,
解得OA=2,
故⊙O的半径为2.
(2)证明:在BM上截取BE=BC,连接CE,如图②.
∵∠ABC=120°,BM平分∠ABC,
∴∠MBC=∠ABM=∠ABC=60°.
又∵BE=BC,
∴△EBC是等边三角形,
∴EC=BC=BE,∠BCE=60°,
∴∠BCD+∠DCE=60°.
∵∠ACM=∠ABM=60°,
∴∠ECM+∠DCE=60°,
∴∠ECM=∠BCD.
∵∠MAC=∠MBC=60°,∠AMC=60°,
∴∠MAC=∠AMC=∠ACM,
∴△ACM是等边三角形,∴AC=MC.
在△ACB和△MCE中,
∴△ACB≌△MCE,
∴AB=ME.
∵ME+BE=BM,
∴AB+BC=BM.
同课章节目录
