全国人教版数学九年级上册课课练:23章 旋转 综合检测(word、含答案解析)
文档属性
| 名称 | 全国人教版数学九年级上册课课练:23章 旋转 综合检测(word、含答案解析) | 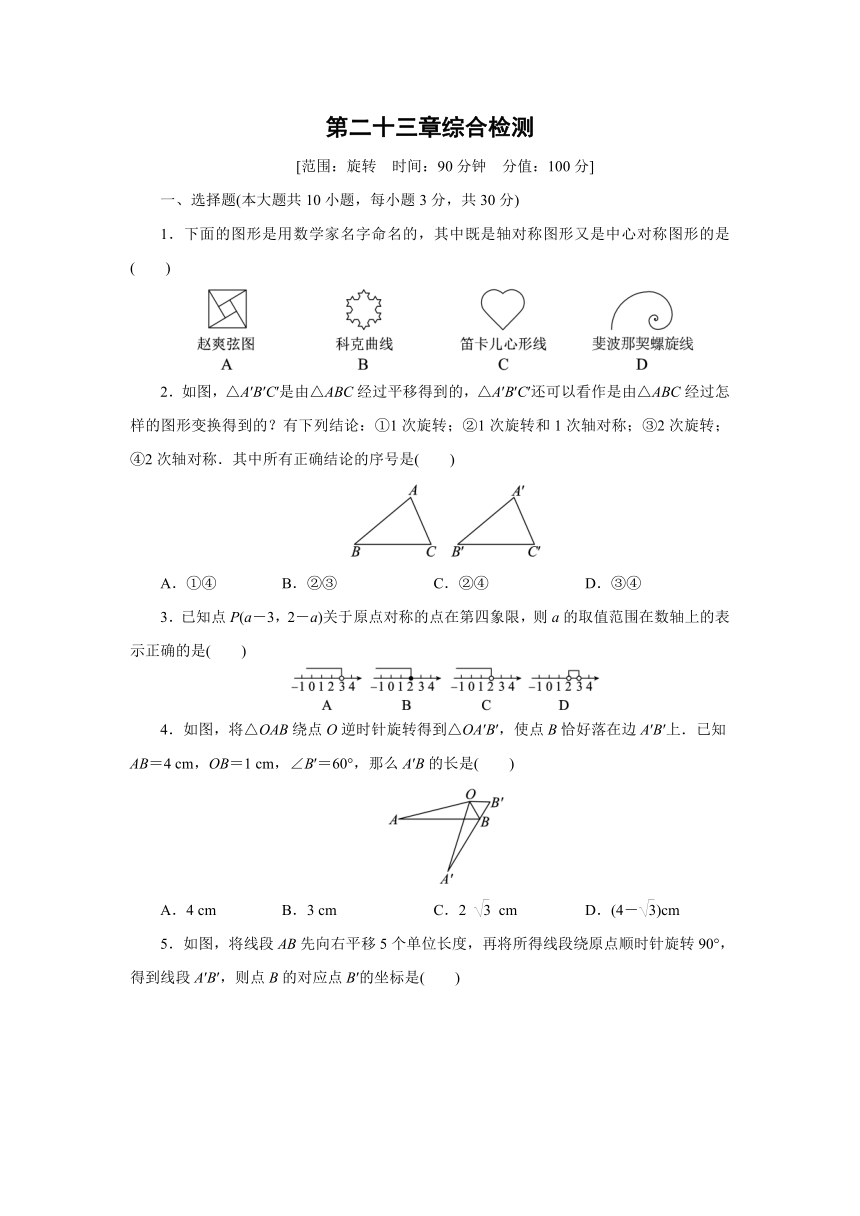 | |
| 格式 | docx | ||
| 文件大小 | 983.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 10:08:38 | ||
图片预览



文档简介
第二十三章综合检测
[范围:旋转 时间:90分钟 分值:100分]
一、选择题(本大题共10小题,每小题3分,共30分)
1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
2.如图,△A′B′C′是由△ABC经过平移得到的,△A′B′C′还可以看作是由△ABC经过怎样的图形变换得到的?有下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )
A.①④ B.②③ C.②④ D.③④
3.已知点P(a-3,2-a)关于原点对称的点在第四象限,则a的取值范围在数轴上的表示正确的是( )
4.如图,将△OAB绕点O逆时针旋转得到△OA′B′,使点B恰好落在边A′B′上.已知AB=4 cm,OB=1 cm,∠B′=60°,那么A′B的长是( )
A.4 cm B.3 cm C.2 cm D.(4-)cm
5.如图,将线段AB先向右平移5个单位长度,再将所得线段绕原点顺时针旋转90°,得到线段A′B′,则点B的对应点B′的坐标是( )
A.(-4,1) B.(-1,2) C.(4,-1) D.(1,-2)
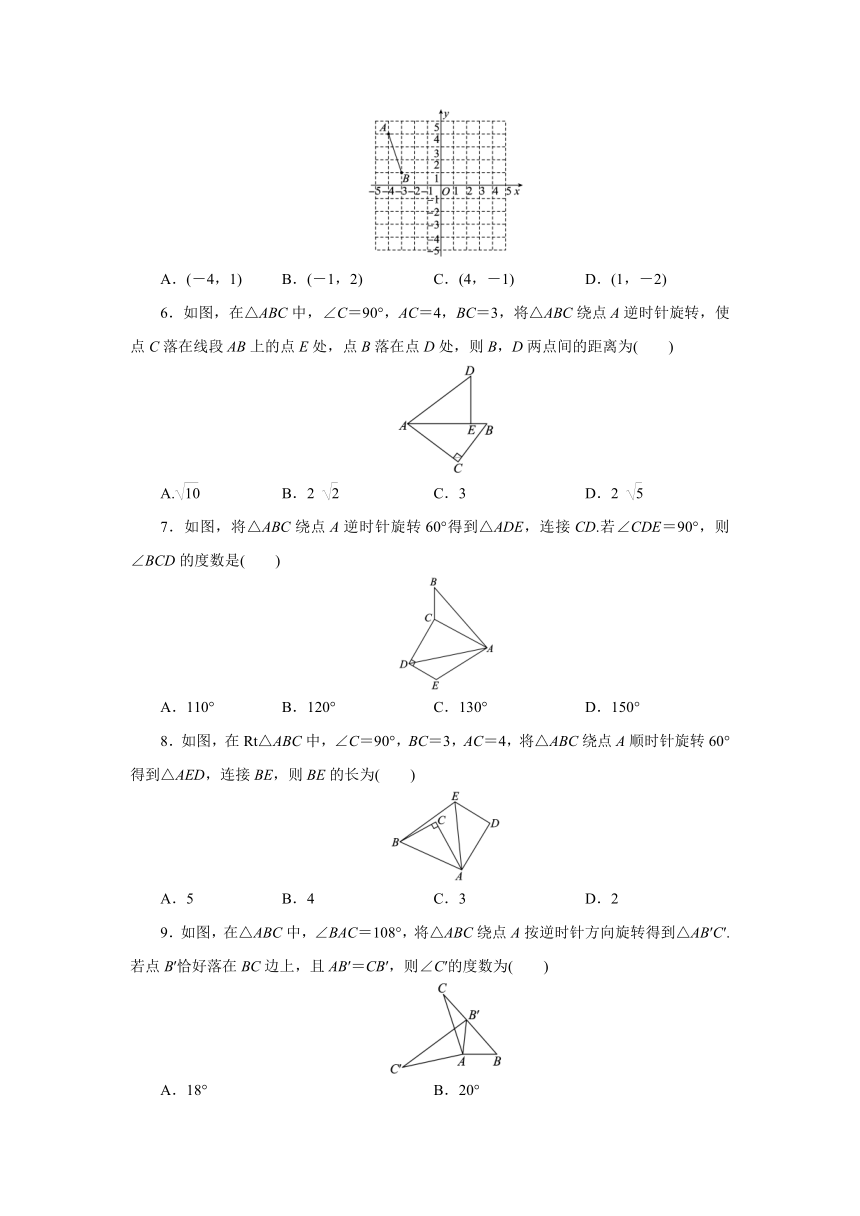
6.如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )
A. B.2 C.3 D.2
7.如图,将△ABC绕点A逆时针旋转60°得到△ADE,连接CD.若∠CDE=90°,则∠BCD的度数是( )
A.110° B.120° C.130° D.150°
8.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,将△ABC绕点A顺时针旋转60°得到△AED,连接BE,则BE的长为( )
A.5 B.4 C.3 D.2
9.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为( )
A.18° B.20°
C.24° D.28°
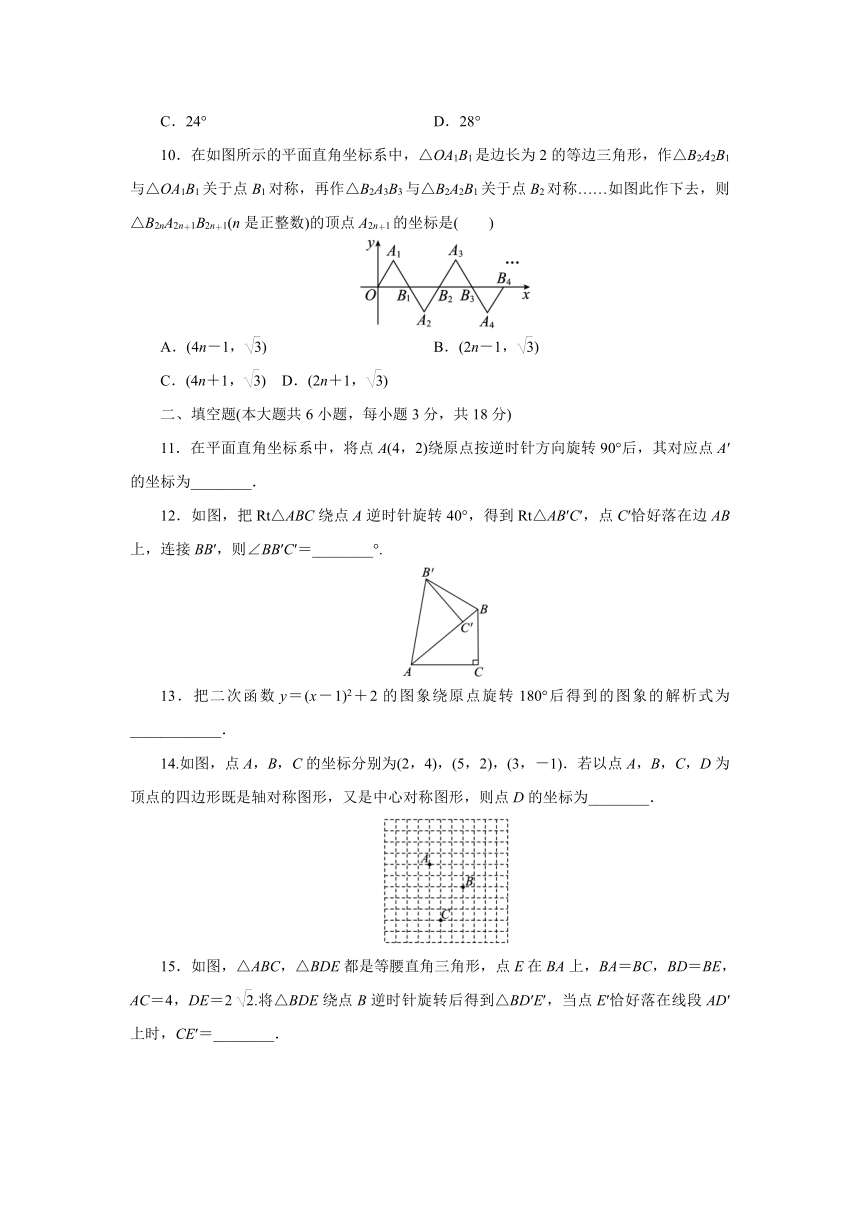
10.在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1对称,再作△B2A3B3与△B2A2B1关于点B2对称……如图此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A.(4n-1,) B.(2n-1,)
C.(4n+1,) D.(2n+1,)
二、填空题(本大题共6小题,每小题3分,共18分)
11.在平面直角坐标系中,将点A(4,2)绕原点按逆时针方向旋转90°后,其对应点A′的坐标为________.
12.如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=________°.
13.把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的解析式为____________.
14.如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为________.
15.如图,△ABC,△BDE都是等腰直角三角形,点E在BA上,BA=BC,BD=BE,AC=4,DE=2 .将△BDE绕点B逆时针旋转后得到△BD′E′,当点E′恰好落在线段AD′上时,CE′=________.
16.如图,两块完全相同的含30°角的三角尺ABC和A′B′C′重合在一起,将三角尺A′B′C′绕其顶点C′逆时针旋转角α(0°<α≤90°),有以下三个结论:①当α=30°时,A′C与AB的交点恰好为AB的中点;②当α=60°时,A′B′恰好经过点B;③在旋转过程中,始终存在AA′⊥BB′.其中正确结论的序号是__________.
三、解答题(本大题共7小题,共52分)
17.(6分)如图,将一个钝角三角形ABC(其中∠ABC=120°)绕点B顺时针旋转得到△A1BC1,使得点C落在AB的延长线上的点C1处,连接AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
18.(6分)如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出点P的坐标.
19.(7分)如图,将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转角α(0°<α<120°)得到线段AD,连接CD,BD.
(1)若α=80°,求∠BDC的度数;
(2)请探究∠BDC的大小是否与角α的大小有关,并说明理由.
20.(8分)如图,在△ABC中,∠BAC=90°,AB=AC,D,E是BC边上的点,将△ABD绕点A逆时针旋转得到△ACD′,连接D′E.
(1)求∠DAD′的度数;
(2)当∠DAE=45°时,求证:DE=D′E.
21.(8分)如图,在△ABC中,∠ACB=135°,BC=1,AC=2,将△ABC绕点A顺时针旋转90°,得到△AED,连接CD,CE.
(1)求CD的长;
(2)求四边形ACED的面积.
22.(8分)如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,交AC于点E.
(1)∠ACM=________;
(2)求BM的长度及∠MBC的度数.
23.(9分)【问题发现】在某次数学兴趣小组活动中,小明同学遇到了如图下问题:
(1)如图①,在等边三角形ABC中,点P在其内部,且PA=3,PC=4,∠APC=150°,求PB的长.经过观察、分析、思考,小明对上述问题形成了如图下想法:将△APC绕点A按顺时针方向旋转60°,得到△ADB,连接PD,寻找PA,PB,PC三者之间的数量关系……
请你根据上述分析过程,完成该问题的解答过程;
【学以致用】参考小明思考问题的方法,解决下面的问题:
(2)如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积;
(3)如图③,在Rt△ABC中,∠ACB=90°,AC=BC,点P在△ABC内,且PA=1,PB=,PC=2 ,求AB的长.
答案
1.B
2.D 连接B′C.先将△ABC绕着B′C的中点旋转180°,再将所得的三角形绕着B′C′的中点旋转180°,即可得到△A′B′C′;先将△ABC沿着B′C的垂直平分线翻折,再将所得的三角形沿着B′C′的垂直平分线翻折,即可得到△A′B′C′.故选D.
3.C
4.B ∵旋转前、后的两个图形是全等图形,AB=4 cm,OB=1 cm,∴A′B′=AB=4 cm,OB′=OB=1 cm.
在△OB′B中,∵∠B′=60°,OB′=OB,
∴△OB′B是等边三角形,∴BB′=OB=1 cm,
∴A′B=A′B′-BB′=4-1=3(cm).
5.D
6.A ∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB=5.
∵将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,
∴∠AED=∠C=90°,AE=AC=4,DE=BC=3,
∴BE=1.
连接BD.在Rt△BED中,BD==.故选A.
7.D
8.A ∵∠C=90°,BC=3,AC=4,
∴AB===5.
∵将△ABC绕点A顺时针旋转60°得到△AED,
∴AE=AB=5,∠BAE=60°,
∴△ABE是等边三角形,
∴BE=AB=5.
9.C ∵AB′=CB′,
∴∠C=∠CAB′,
∴∠AB′B=∠C+∠CAB′=2∠C.
∵将△ABC绕点A按逆时针方向旋转得到△AB′C′,
∴∠C=∠C′,AB=AB′,
∴∠B=∠AB′B=2∠C.
∵∠B+∠C+∠BAC=180°,
∴3∠C=180°-108°,
∴∠C=24°,
∴∠C′=∠C=24°.
10.C 由题意易知A1(1,),A2(3,-),A3(5,),A4(7,-),…,
∴点An的坐标为
∵2n+1是奇数,∴点A2n+1的坐标是(4n+1,).故选C.
11.(-2,4)
12.20 由旋转的性质可知AB=AB′,∠BAB′=40°,∠AC′B′=∠ACB=90°,
∴∠ABB′=70°,∴∠BB′C′=20°.
13.y=-x2-2x-3 旋转前二次项的系数a=1,抛物线的顶点坐标是(1,2),旋转后二次项的系数a=-1,抛物线的顶点坐标是(-1,-2),∴新抛物线的解析式为y=-(x+1)2-2,即y=-x2-2x-3.
14.(0,1)
15.+ 如图,连接CE′.
∵△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2 ,
∴∠EDB=45°,AB=BC=2 ,BD=BE=2.
∵将△BDE绕点B逆时针旋转后得到△BD′E′,
∴D′B=BE′=BD=2,∠D′BE′=90°=∠ABC,
∠D′=∠EDB=45°,
∴∠ABD′=∠CBE′,
∴△ABD′≌△CBE′(SAS),
∴∠D′=∠CE′B=45°.
过点B作BH⊥CE′于点H,
在Rt△BHE′中,BH=E′H=BE′=,
在Rt△BCH中,CH==,
∴CE′=+.故答案为+.
16.①②③
17.解:(1)旋转角的度数为60°.
(2)证明:由旋转的性质知∠ABC=∠A1BC1=120°,∠C=∠C1,AB=A1B.
∵点A,B,C1在同一直线上,
∴∠ABC1=180°,
∴∠ABA1=∠CBC1=60°,∴∠A1BC=60°.
∵AB=A1B,∠ABA1=60°,
∴△ABA1是等边三角形,
∴∠AA1B=60°=∠A1BC,
∴AA1∥BC,∴∠A1AC=∠C.
又∵∠C=∠C1,∴∠A1AC=∠C1.
18.解:(1)△A1B1C1如图所示.
(2)△A2B2C2如图所示.
(3)△PAB如图所示,点P的坐标是(2,0).
19.解:(1)由旋转的性质可知AC=AD,
∠CAD=80°,
∴∠ADC=∠ACD=×(180°-80°)=50°.
∵∠BAD=∠BAC+∠CAD=60°+80°=140°,又AB=AD,
∴∠B=∠ADB=×(180°-140°)=20°,
∴∠BDC=∠ADC-∠ADB=50°-20°=30°.
(2)结论:∠BDC的大小与角α的大小无关.
理由:由旋转的性质可知AB=AC=AD,∠BAC=∠CAD=α,∴∠ADC=∠ACD=(180°-α),∠BAD=∠BAC+∠CAD=60°+α,
∴∠B=∠ADB=(180°-60°-α)=(120°-α),
∴∠BDC=∠ADC-∠ADB=(180°-α)-(120°-α)=30°,
∴∠BDC的大小与角α的大小无关.
20.解:(1)∵将△ABD绕点A逆时针旋转得到△ACD′,
∴∠DAD′=∠BAC.
∵∠BAC=90°,
∴∠DAD′=90°.
(2)证明:∵△ABD绕点A逆时针旋转得到△ACD′,
∴AD=AD′,∠DAD′=∠BAC=90°.
∵∠DAE=45°,
∴∠D′AE=∠DAD′-∠DAE=90°-45°=45°,∴∠D′AE=∠DAE.
在△AED与△AED′中,
∴△AED≌△AED′(SAS),
∴DE=D′E.
21.解:(1)根据旋转的性质,得AD=AC=2,∠CAD=90°,
∴△ACD是等腰直角三角形,
根据勾股定理,得
CD===2 .
(2)根据旋转的性质,得∠ADE=∠ACB=135°,DE=BC=1.
由(1)知,CD=2 ,∠ADC=45°,
∴∠CDE=∠ADE-∠ADC=90°,
∴S四边形ACED=S△ACD+S△CDE=AC·AD+CD·DE=×2×2+×2 ×1=2+.
22.解:(1)60°
(2)连接AM,如图.
∵△ABC绕点C逆时针旋转60°,得到△MNC,
∴∠ACM=60°,AC=MC,
∴△ACM为等边三角形,∴MA=MC.
又∵AB=BC,
∴BM垂直平分AC,即AC⊥BM,AE=CE.
∵∠ABC=90°,AB=BC=2,
∴AC=2 ,BM平分∠ABC,
∴∠MBC=45°,CE=AE=BE=AC=,MC=AC=2 .
在Rt△CME中,ME===,
∴BM=BE+ME=+.
故BM的长度为+,∠MBC的度数为45°.
23.解:(1)将△APC绕点A按顺时针方向旋转60°,得到△ADB,连接PD,
则AD=PA=3,BD=PC=4,∠ADB=∠APC=150°,∠PAD=60°,
∴△APD是等边三角形,
∴∠ADP=60°,DP=PA=3,
∴∠PDB=90°,
∴PB===5.
(2)将△APB绕点A按逆时针方向旋转60°,得到△AP′C,连接PP′,如图①所示,
则AP=AP′,∠PAP′=60°,∠AP′C=∠APB=360°-90°-120°=150°,
∴△APP′是等边三角形,
∴PP′=AP,∠AP′P=∠APP′=60°.
∵∠APC=90°,∠AP′C=150°,
∴∠PP′C=90°,∠P′PC=30°,
∴PP′=PC,即AP=PC.
∵∠APC=90°,
∴AP2+PC2=AC2,即(PC)2+PC2=72,
∴PC=2 ,∴AP=,
∴S△APC=AP·PC=××2 =7 .
(3)如图②,把△ACP绕点C逆时针旋转90°得到△BCD,连接PD.
由旋转的性质可知:BD=PA=1,CD=PC=2 ,∠CDB=∠CPA,∠PCD=90°,
∴△PCD是等腰直角三角形,
∴PD==4,∠CDP=∠CPD=45°.
∵PD2+BD2=42+12=17,PB2=()2=17,
∴PD2+BD2=PB2,
∴∠PDB=90°,
∴∠CDB=135°,
∴∠CPA=∠CDB=135°.
又∵∠CPD=45°,
∴∠CPA+∠CPD=180°,
∴A,P,D三点共线,
∴AD=AP+PD=5,
在Rt△ADB中,AB===.
[范围:旋转 时间:90分钟 分值:100分]
一、选择题(本大题共10小题,每小题3分,共30分)
1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
2.如图,△A′B′C′是由△ABC经过平移得到的,△A′B′C′还可以看作是由△ABC经过怎样的图形变换得到的?有下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )
A.①④ B.②③ C.②④ D.③④
3.已知点P(a-3,2-a)关于原点对称的点在第四象限,则a的取值范围在数轴上的表示正确的是( )
4.如图,将△OAB绕点O逆时针旋转得到△OA′B′,使点B恰好落在边A′B′上.已知AB=4 cm,OB=1 cm,∠B′=60°,那么A′B的长是( )
A.4 cm B.3 cm C.2 cm D.(4-)cm
5.如图,将线段AB先向右平移5个单位长度,再将所得线段绕原点顺时针旋转90°,得到线段A′B′,则点B的对应点B′的坐标是( )
A.(-4,1) B.(-1,2) C.(4,-1) D.(1,-2)
6.如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )
A. B.2 C.3 D.2
7.如图,将△ABC绕点A逆时针旋转60°得到△ADE,连接CD.若∠CDE=90°,则∠BCD的度数是( )
A.110° B.120° C.130° D.150°
8.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,将△ABC绕点A顺时针旋转60°得到△AED,连接BE,则BE的长为( )
A.5 B.4 C.3 D.2
9.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为( )
A.18° B.20°
C.24° D.28°
10.在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1对称,再作△B2A3B3与△B2A2B1关于点B2对称……如图此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A.(4n-1,) B.(2n-1,)
C.(4n+1,) D.(2n+1,)
二、填空题(本大题共6小题,每小题3分,共18分)
11.在平面直角坐标系中,将点A(4,2)绕原点按逆时针方向旋转90°后,其对应点A′的坐标为________.
12.如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=________°.
13.把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的解析式为____________.
14.如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为________.
15.如图,△ABC,△BDE都是等腰直角三角形,点E在BA上,BA=BC,BD=BE,AC=4,DE=2 .将△BDE绕点B逆时针旋转后得到△BD′E′,当点E′恰好落在线段AD′上时,CE′=________.
16.如图,两块完全相同的含30°角的三角尺ABC和A′B′C′重合在一起,将三角尺A′B′C′绕其顶点C′逆时针旋转角α(0°<α≤90°),有以下三个结论:①当α=30°时,A′C与AB的交点恰好为AB的中点;②当α=60°时,A′B′恰好经过点B;③在旋转过程中,始终存在AA′⊥BB′.其中正确结论的序号是__________.
三、解答题(本大题共7小题,共52分)
17.(6分)如图,将一个钝角三角形ABC(其中∠ABC=120°)绕点B顺时针旋转得到△A1BC1,使得点C落在AB的延长线上的点C1处,连接AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
18.(6分)如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出点P的坐标.
19.(7分)如图,将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转角α(0°<α<120°)得到线段AD,连接CD,BD.
(1)若α=80°,求∠BDC的度数;
(2)请探究∠BDC的大小是否与角α的大小有关,并说明理由.
20.(8分)如图,在△ABC中,∠BAC=90°,AB=AC,D,E是BC边上的点,将△ABD绕点A逆时针旋转得到△ACD′,连接D′E.
(1)求∠DAD′的度数;
(2)当∠DAE=45°时,求证:DE=D′E.
21.(8分)如图,在△ABC中,∠ACB=135°,BC=1,AC=2,将△ABC绕点A顺时针旋转90°,得到△AED,连接CD,CE.
(1)求CD的长;
(2)求四边形ACED的面积.
22.(8分)如图,在Rt△ABC中,∠ABC=90°,AB=BC=2,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,交AC于点E.
(1)∠ACM=________;
(2)求BM的长度及∠MBC的度数.
23.(9分)【问题发现】在某次数学兴趣小组活动中,小明同学遇到了如图下问题:
(1)如图①,在等边三角形ABC中,点P在其内部,且PA=3,PC=4,∠APC=150°,求PB的长.经过观察、分析、思考,小明对上述问题形成了如图下想法:将△APC绕点A按顺时针方向旋转60°,得到△ADB,连接PD,寻找PA,PB,PC三者之间的数量关系……
请你根据上述分析过程,完成该问题的解答过程;
【学以致用】参考小明思考问题的方法,解决下面的问题:
(2)如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积;
(3)如图③,在Rt△ABC中,∠ACB=90°,AC=BC,点P在△ABC内,且PA=1,PB=,PC=2 ,求AB的长.
答案
1.B
2.D 连接B′C.先将△ABC绕着B′C的中点旋转180°,再将所得的三角形绕着B′C′的中点旋转180°,即可得到△A′B′C′;先将△ABC沿着B′C的垂直平分线翻折,再将所得的三角形沿着B′C′的垂直平分线翻折,即可得到△A′B′C′.故选D.
3.C
4.B ∵旋转前、后的两个图形是全等图形,AB=4 cm,OB=1 cm,∴A′B′=AB=4 cm,OB′=OB=1 cm.
在△OB′B中,∵∠B′=60°,OB′=OB,
∴△OB′B是等边三角形,∴BB′=OB=1 cm,
∴A′B=A′B′-BB′=4-1=3(cm).
5.D
6.A ∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB=5.
∵将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,
∴∠AED=∠C=90°,AE=AC=4,DE=BC=3,
∴BE=1.
连接BD.在Rt△BED中,BD==.故选A.
7.D
8.A ∵∠C=90°,BC=3,AC=4,
∴AB===5.
∵将△ABC绕点A顺时针旋转60°得到△AED,
∴AE=AB=5,∠BAE=60°,
∴△ABE是等边三角形,
∴BE=AB=5.
9.C ∵AB′=CB′,
∴∠C=∠CAB′,
∴∠AB′B=∠C+∠CAB′=2∠C.
∵将△ABC绕点A按逆时针方向旋转得到△AB′C′,
∴∠C=∠C′,AB=AB′,
∴∠B=∠AB′B=2∠C.
∵∠B+∠C+∠BAC=180°,
∴3∠C=180°-108°,
∴∠C=24°,
∴∠C′=∠C=24°.
10.C 由题意易知A1(1,),A2(3,-),A3(5,),A4(7,-),…,
∴点An的坐标为
∵2n+1是奇数,∴点A2n+1的坐标是(4n+1,).故选C.
11.(-2,4)
12.20 由旋转的性质可知AB=AB′,∠BAB′=40°,∠AC′B′=∠ACB=90°,
∴∠ABB′=70°,∴∠BB′C′=20°.
13.y=-x2-2x-3 旋转前二次项的系数a=1,抛物线的顶点坐标是(1,2),旋转后二次项的系数a=-1,抛物线的顶点坐标是(-1,-2),∴新抛物线的解析式为y=-(x+1)2-2,即y=-x2-2x-3.
14.(0,1)
15.+ 如图,连接CE′.
∵△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2 ,
∴∠EDB=45°,AB=BC=2 ,BD=BE=2.
∵将△BDE绕点B逆时针旋转后得到△BD′E′,
∴D′B=BE′=BD=2,∠D′BE′=90°=∠ABC,
∠D′=∠EDB=45°,
∴∠ABD′=∠CBE′,
∴△ABD′≌△CBE′(SAS),
∴∠D′=∠CE′B=45°.
过点B作BH⊥CE′于点H,
在Rt△BHE′中,BH=E′H=BE′=,
在Rt△BCH中,CH==,
∴CE′=+.故答案为+.
16.①②③
17.解:(1)旋转角的度数为60°.
(2)证明:由旋转的性质知∠ABC=∠A1BC1=120°,∠C=∠C1,AB=A1B.
∵点A,B,C1在同一直线上,
∴∠ABC1=180°,
∴∠ABA1=∠CBC1=60°,∴∠A1BC=60°.
∵AB=A1B,∠ABA1=60°,
∴△ABA1是等边三角形,
∴∠AA1B=60°=∠A1BC,
∴AA1∥BC,∴∠A1AC=∠C.
又∵∠C=∠C1,∴∠A1AC=∠C1.
18.解:(1)△A1B1C1如图所示.
(2)△A2B2C2如图所示.
(3)△PAB如图所示,点P的坐标是(2,0).
19.解:(1)由旋转的性质可知AC=AD,
∠CAD=80°,
∴∠ADC=∠ACD=×(180°-80°)=50°.
∵∠BAD=∠BAC+∠CAD=60°+80°=140°,又AB=AD,
∴∠B=∠ADB=×(180°-140°)=20°,
∴∠BDC=∠ADC-∠ADB=50°-20°=30°.
(2)结论:∠BDC的大小与角α的大小无关.
理由:由旋转的性质可知AB=AC=AD,∠BAC=∠CAD=α,∴∠ADC=∠ACD=(180°-α),∠BAD=∠BAC+∠CAD=60°+α,
∴∠B=∠ADB=(180°-60°-α)=(120°-α),
∴∠BDC=∠ADC-∠ADB=(180°-α)-(120°-α)=30°,
∴∠BDC的大小与角α的大小无关.
20.解:(1)∵将△ABD绕点A逆时针旋转得到△ACD′,
∴∠DAD′=∠BAC.
∵∠BAC=90°,
∴∠DAD′=90°.
(2)证明:∵△ABD绕点A逆时针旋转得到△ACD′,
∴AD=AD′,∠DAD′=∠BAC=90°.
∵∠DAE=45°,
∴∠D′AE=∠DAD′-∠DAE=90°-45°=45°,∴∠D′AE=∠DAE.
在△AED与△AED′中,
∴△AED≌△AED′(SAS),
∴DE=D′E.
21.解:(1)根据旋转的性质,得AD=AC=2,∠CAD=90°,
∴△ACD是等腰直角三角形,
根据勾股定理,得
CD===2 .
(2)根据旋转的性质,得∠ADE=∠ACB=135°,DE=BC=1.
由(1)知,CD=2 ,∠ADC=45°,
∴∠CDE=∠ADE-∠ADC=90°,
∴S四边形ACED=S△ACD+S△CDE=AC·AD+CD·DE=×2×2+×2 ×1=2+.
22.解:(1)60°
(2)连接AM,如图.
∵△ABC绕点C逆时针旋转60°,得到△MNC,
∴∠ACM=60°,AC=MC,
∴△ACM为等边三角形,∴MA=MC.
又∵AB=BC,
∴BM垂直平分AC,即AC⊥BM,AE=CE.
∵∠ABC=90°,AB=BC=2,
∴AC=2 ,BM平分∠ABC,
∴∠MBC=45°,CE=AE=BE=AC=,MC=AC=2 .
在Rt△CME中,ME===,
∴BM=BE+ME=+.
故BM的长度为+,∠MBC的度数为45°.
23.解:(1)将△APC绕点A按顺时针方向旋转60°,得到△ADB,连接PD,
则AD=PA=3,BD=PC=4,∠ADB=∠APC=150°,∠PAD=60°,
∴△APD是等边三角形,
∴∠ADP=60°,DP=PA=3,
∴∠PDB=90°,
∴PB===5.
(2)将△APB绕点A按逆时针方向旋转60°,得到△AP′C,连接PP′,如图①所示,
则AP=AP′,∠PAP′=60°,∠AP′C=∠APB=360°-90°-120°=150°,
∴△APP′是等边三角形,
∴PP′=AP,∠AP′P=∠APP′=60°.
∵∠APC=90°,∠AP′C=150°,
∴∠PP′C=90°,∠P′PC=30°,
∴PP′=PC,即AP=PC.
∵∠APC=90°,
∴AP2+PC2=AC2,即(PC)2+PC2=72,
∴PC=2 ,∴AP=,
∴S△APC=AP·PC=××2 =7 .
(3)如图②,把△ACP绕点C逆时针旋转90°得到△BCD,连接PD.
由旋转的性质可知:BD=PA=1,CD=PC=2 ,∠CDB=∠CPA,∠PCD=90°,
∴△PCD是等腰直角三角形,
∴PD==4,∠CDP=∠CPD=45°.
∵PD2+BD2=42+12=17,PB2=()2=17,
∴PD2+BD2=PB2,
∴∠PDB=90°,
∴∠CDB=135°,
∴∠CPA=∠CDB=135°.
又∵∠CPD=45°,
∴∠CPA+∠CPD=180°,
∴A,P,D三点共线,
∴AD=AP+PD=5,
在Rt△ADB中,AB===.
同课章节目录
