直线和圆(复习)-圆的方程复习[上学期]
文档属性
| 名称 | 直线和圆(复习)-圆的方程复习[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 154.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-01-03 06:05:00 | ||
图片预览






文档简介
课件21张PPT。直线与圆、圆与圆的位置关系---复习则圆C与l相离?Δ<0,
圆C与l 相切?Δ=0,
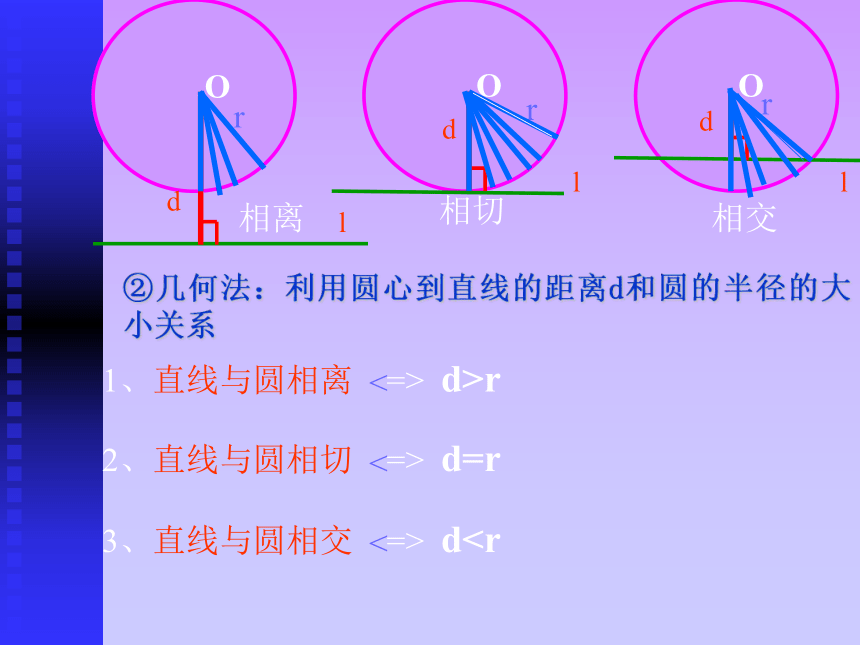
圆C与l 相交??Δ>0.(1)直线与圆的位置关系有三种:相离,相切,相交。判断直线与圆的位置关系的方法常见的有两种方法:1.直线与圆的位置关系①代数法: 由圆C方程及直线L的方程,消去一个未知数,得一元二次方程,设一元二次方程的根的判别式为Δddd.O.O.Orrr相离相切相交1、直线与圆相离 => d>r2、直线与圆相切 => d=r3、直线与圆相交 => d<
<
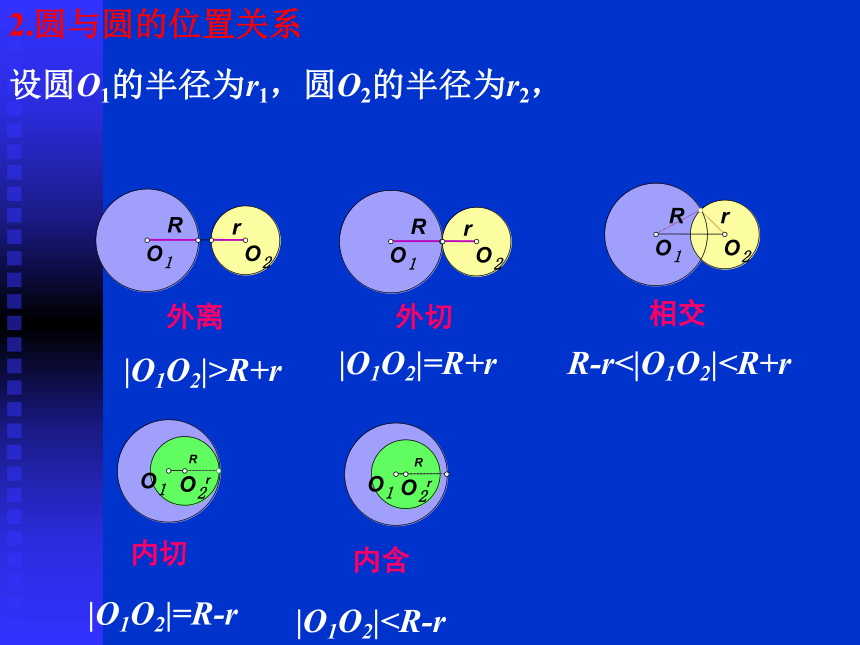
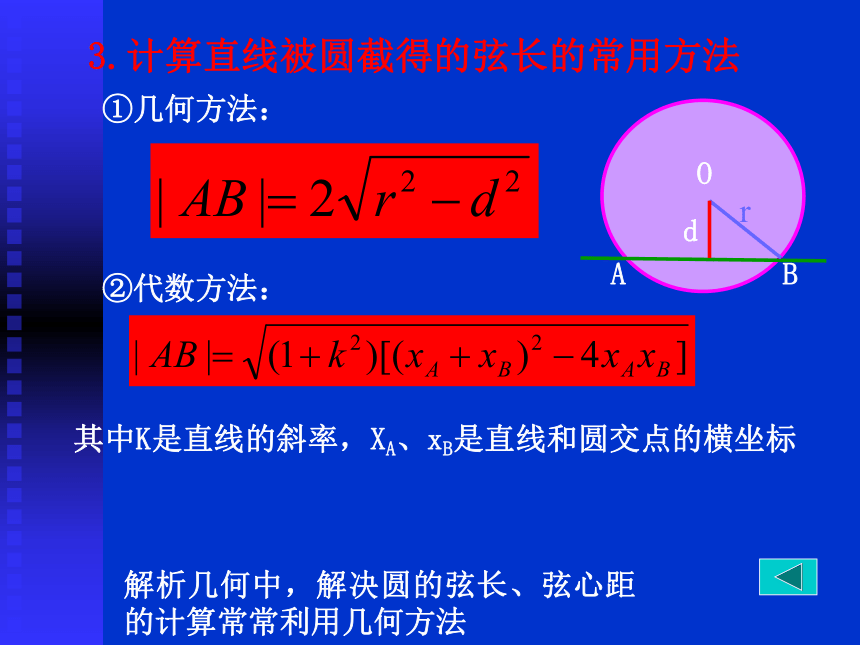
lll②几何法:利用圆心到直线的距离d和圆的半径的大小关系外离|O1O2|>R+r|O1O2|=R+rR-r<|O1O2|设圆O1的半径为r1,圆O2的半径为r2,3.计算直线被圆截得的弦长的常用方法①几何方法:②代数方法:解析几何中,解决圆的弦长、弦心距的计算常常利用几何方法其中K是直线的斜率,XA、xB是直线和圆交点的横坐标①圆x2+y2=r2,圆上一点为(x0,y0),则此点的切线方程为x0x+y0y=r2.②圆(x-a)2+(y-b)2=r2,圆上一点为(x0,y0),则过此点的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.4.过圆上一点的切线方程:
返回5. 相交弦方程
⊙O1:x2+y2+D1x+E1y+F1=0和
⊙O2:x2+y2+D2x+E2y+F2=0相交时,
公共弦方程为(D1-D2)x+(E1-E2)y+(F1-F2)=0. 6.圆系方程:
①设圆C1∶x2+y2+D1x+E1y+F1=0和圆C2∶x2+y2+D2x+E2y+F2=0.若两圆相交,则过交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0 (λ为参数,圆系中不包括圆C2,λ=-1为两圆的公共弦所在直线方程).
②设圆C∶x2+y2+Dx+Ey+F=0与直线l:Ax+By+C=0,若直线与圆相交,则过交点的圆系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0(λ为参数).
返回例1.已知圆C:(x-1)2+(y-2)2=25,
直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R)
(1)证明不论m取何值,直线l与圆恒交于两点
(2)求直线被圆C截得的弦长最小时l的方程(1)解法1:解法2:∴直线l与圆恒交于两点分析:对于直线和圆的位置关系的判断,除了用代数法或几何法。由于本题直线与圆恒交于两点,则可以考虑直线恒过圆内定点。解法3:(1)直线l的方程可化为(x+y-4)+m(2x+y-7)=0所以点A在圆C的内部,从而直线l与圆恒交于两点(2)若直线L交圆与B、D两点,则弦长得直线l的方程是2x-y-5=0当弦长|BD|最小时,d最大,则l⊥AC例2.如图自点A(-3,3)发出的光线L射到x轴上,被X轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求射线L的直线方程解法1:由已知圆的标准方程是(x-2)2+(y-2)2=1设光线L所在直线的方程是y-3=k(x+3),则k≠0整理得kx+y+3k+3=0这条直线与已知圆相切,所以圆心到直线的距离等于半径1即:3x+4y-3=0或4x+3y+3=0解法2:由已知圆的标准方程是(x-2)2+(y-2)2=1所以圆C关于x轴的对称圆C’:(x-2)2+(y+2)2=1令l的方程:y-3=k(x+3),即kx-y+3+3k=0所以直线l与圆C’相切所求直线的方程是3x+4y-3=0或4x+3y+3=0解法3:点A(-3,3)关于x轴的对称点A’(-3,-3)在反射光线的反向延长线上,所以设反射光线所在直线的方程为y+3=k(x+3)即kx-y+3k-3=0所以L的斜率所求直线的方程是3x+4y-3=0或4x+3y+3=0返回例3. 求以圆C1∶x2+y2-12x-2y-13=0和圆C2:x2+y2+12x+16y-25=0的公共弦为直径的圆的方程.
解法一: 相减得公共弦所在直线方程为4x+3y-2=0. ∵所求圆以AB为直径, 于是圆的方程为(x-2)2+(y+2)2=25 .返回解法二:
设所求圆的方程为:
x2+y2-12x-2y-13+λ(x2+y2+12x+16y-25)=0(λ为参数) ∵圆心C应在公共弦AB所在直线上, ∴ 所求圆的方程为x2+y2-4x+4y-17=0. 1?在圆x2+y2=4上,与直线4x+3y-12=0的距离最小的点的坐标是( )?
(A)8/5,6/5 (B)8/5,-6/5?
(C)-8/5,6/5 (D)-8/5,-6/5A? 2?已知⊙O1:x2+y2=2 ⊙O2:(x-2)2+(y-3)2=1,则以M(1,1)为切点的⊙O1的切线方程为 ,过点M作⊙O2的切线,其方程为 ,此时M点到切点的距离为 .? ? 2?已知⊙O1:x2+y2=2 ⊙O2:(x-2)2+(y-3)2=1,则以M(1,1)为切点的⊙O1的切线方程为x+y= 2,过点M作⊙O2的切线,其方程为3x-4y+1=0和x=1,此时M点到切点的距离为2.? 练习3.两圆x2+y2-6x+4y+12=0和x2+y2-14x-12y+14=0的位置关系是( )
(A)相离 (B)外切 (C)相交 (D)内切CC返回5.直线3x+4y+m=0与圆x2+y2-5y=0交于两点A、B,且OA⊥OB
(O为原点),求m的值.返回返回6.过点P(-2,-3)作圆C:(x-4)2+(y-2)2=9的两条切线,切点分别为A、B.求:
(1)经过圆心C,切点A、B这三点的圆的方程;
(2)直线AB的方程;
(3)线段AB的长.
圆C与l 相切?Δ=0,
圆C与l 相交??Δ>0.(1)直线与圆的位置关系有三种:相离,相切,相交。判断直线与圆的位置关系的方法常见的有两种方法:1.直线与圆的位置关系①代数法: 由圆C方程及直线L的方程,消去一个未知数,得一元二次方程,设一元二次方程的根的判别式为Δddd.O.O.Orrr相离相切相交1、直线与圆相离 => d>r2、直线与圆相切 => d=r3、直线与圆相交 => d
<
lll②几何法:利用圆心到直线的距离d和圆的半径的大小关系外离|O1O2|>R+r|O1O2|=R+rR-r<|O1O2|
返回5. 相交弦方程
⊙O1:x2+y2+D1x+E1y+F1=0和
⊙O2:x2+y2+D2x+E2y+F2=0相交时,
公共弦方程为(D1-D2)x+(E1-E2)y+(F1-F2)=0. 6.圆系方程:
①设圆C1∶x2+y2+D1x+E1y+F1=0和圆C2∶x2+y2+D2x+E2y+F2=0.若两圆相交,则过交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0 (λ为参数,圆系中不包括圆C2,λ=-1为两圆的公共弦所在直线方程).
②设圆C∶x2+y2+Dx+Ey+F=0与直线l:Ax+By+C=0,若直线与圆相交,则过交点的圆系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0(λ为参数).
返回例1.已知圆C:(x-1)2+(y-2)2=25,
直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R)
(1)证明不论m取何值,直线l与圆恒交于两点
(2)求直线被圆C截得的弦长最小时l的方程(1)解法1:解法2:∴直线l与圆恒交于两点分析:对于直线和圆的位置关系的判断,除了用代数法或几何法。由于本题直线与圆恒交于两点,则可以考虑直线恒过圆内定点。解法3:(1)直线l的方程可化为(x+y-4)+m(2x+y-7)=0所以点A在圆C的内部,从而直线l与圆恒交于两点(2)若直线L交圆与B、D两点,则弦长得直线l的方程是2x-y-5=0当弦长|BD|最小时,d最大,则l⊥AC例2.如图自点A(-3,3)发出的光线L射到x轴上,被X轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求射线L的直线方程解法1:由已知圆的标准方程是(x-2)2+(y-2)2=1设光线L所在直线的方程是y-3=k(x+3),则k≠0整理得kx+y+3k+3=0这条直线与已知圆相切,所以圆心到直线的距离等于半径1即:3x+4y-3=0或4x+3y+3=0解法2:由已知圆的标准方程是(x-2)2+(y-2)2=1所以圆C关于x轴的对称圆C’:(x-2)2+(y+2)2=1令l的方程:y-3=k(x+3),即kx-y+3+3k=0所以直线l与圆C’相切所求直线的方程是3x+4y-3=0或4x+3y+3=0解法3:点A(-3,3)关于x轴的对称点A’(-3,-3)在反射光线的反向延长线上,所以设反射光线所在直线的方程为y+3=k(x+3)即kx-y+3k-3=0所以L的斜率所求直线的方程是3x+4y-3=0或4x+3y+3=0返回例3. 求以圆C1∶x2+y2-12x-2y-13=0和圆C2:x2+y2+12x+16y-25=0的公共弦为直径的圆的方程.
解法一: 相减得公共弦所在直线方程为4x+3y-2=0. ∵所求圆以AB为直径, 于是圆的方程为(x-2)2+(y+2)2=25 .返回解法二:
设所求圆的方程为:
x2+y2-12x-2y-13+λ(x2+y2+12x+16y-25)=0(λ为参数) ∵圆心C应在公共弦AB所在直线上, ∴ 所求圆的方程为x2+y2-4x+4y-17=0. 1?在圆x2+y2=4上,与直线4x+3y-12=0的距离最小的点的坐标是( )?
(A)8/5,6/5 (B)8/5,-6/5?
(C)-8/5,6/5 (D)-8/5,-6/5A? 2?已知⊙O1:x2+y2=2 ⊙O2:(x-2)2+(y-3)2=1,则以M(1,1)为切点的⊙O1的切线方程为 ,过点M作⊙O2的切线,其方程为 ,此时M点到切点的距离为 .? ? 2?已知⊙O1:x2+y2=2 ⊙O2:(x-2)2+(y-3)2=1,则以M(1,1)为切点的⊙O1的切线方程为x+y= 2,过点M作⊙O2的切线,其方程为3x-4y+1=0和x=1,此时M点到切点的距离为2.? 练习3.两圆x2+y2-6x+4y+12=0和x2+y2-14x-12y+14=0的位置关系是( )
(A)相离 (B)外切 (C)相交 (D)内切CC返回5.直线3x+4y+m=0与圆x2+y2-5y=0交于两点A、B,且OA⊥OB
(O为原点),求m的值.返回返回6.过点P(-2,-3)作圆C:(x-4)2+(y-2)2=9的两条切线,切点分别为A、B.求:
(1)经过圆心C,切点A、B这三点的圆的方程;
(2)直线AB的方程;
(3)线段AB的长.
