苏教版(2019)选择性必修第一册1.2.2 直线的两点式方程 同步练习(Word版含解析)
文档属性
| 名称 | 苏教版(2019)选择性必修第一册1.2.2 直线的两点式方程 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 81.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 00:00:00 | ||
图片预览


文档简介
1.2.2 直线的两点式方程
基础过关练
题组一 直线的两点式方程
1.(2020江苏南京雨花台中学月考)过点M(-4,3)和N(-2,1)的直线的方程是( )
A.x-y+3=0 B.x+y+1=0
C.x-y-1=0 D.x+y-3=0
2.(2020江苏苏州第六中学阶段测试)已知直线l的两点式方程为,则l的斜率为( )
A.-
3.(2020江苏张家港高级中学月考)已知三角形的三个顶点分别是A(4,0),B(6,7),C(0,3),求三边所在直线的方程.
4.一束光线从点A(3,2)发出,经x轴反射后通过点B(-1,6),分别求入射光线和反射光线所在直线的方程.
题组二 直线的截距式方程
5.(2020江苏苏州黄桥中学期中)在x轴和y轴上的截距分别为-4和5的直线的方程是 ( )
A.=1
C.=1
6.(2020吉林长春东北师大附中阶段测试)直线-=-1在x轴、y轴上的截距分别为( )
A.2,3 B.-2,3
C.-2,-3 D.2,-3
7.(2020江苏常州奔牛高级中学阶段测试)若直线=1过第一、三、四象限,则( )
A.a>0,b>0 B.a>0,b<0
C.a<0,b>0 D.a<0,b<0
8.根据下列条件求直线的方程:
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2;
(3)过点(4,1),且在两坐标轴上的截距相等.
能力提升练
题组一 直线的两点式方程和截距式方程
1.(2020江苏苏州震泽中学期末)直线=0在两个坐标轴上的截距之和为( )
A.1 B.5 C.-1 D.0
2.(2020山西怀仁重点中学期末)经过点A(-1,2),并且在两个坐标轴上的截距的绝对值相等的直线的条数是( )
A.1 B.2 C.3 D.4
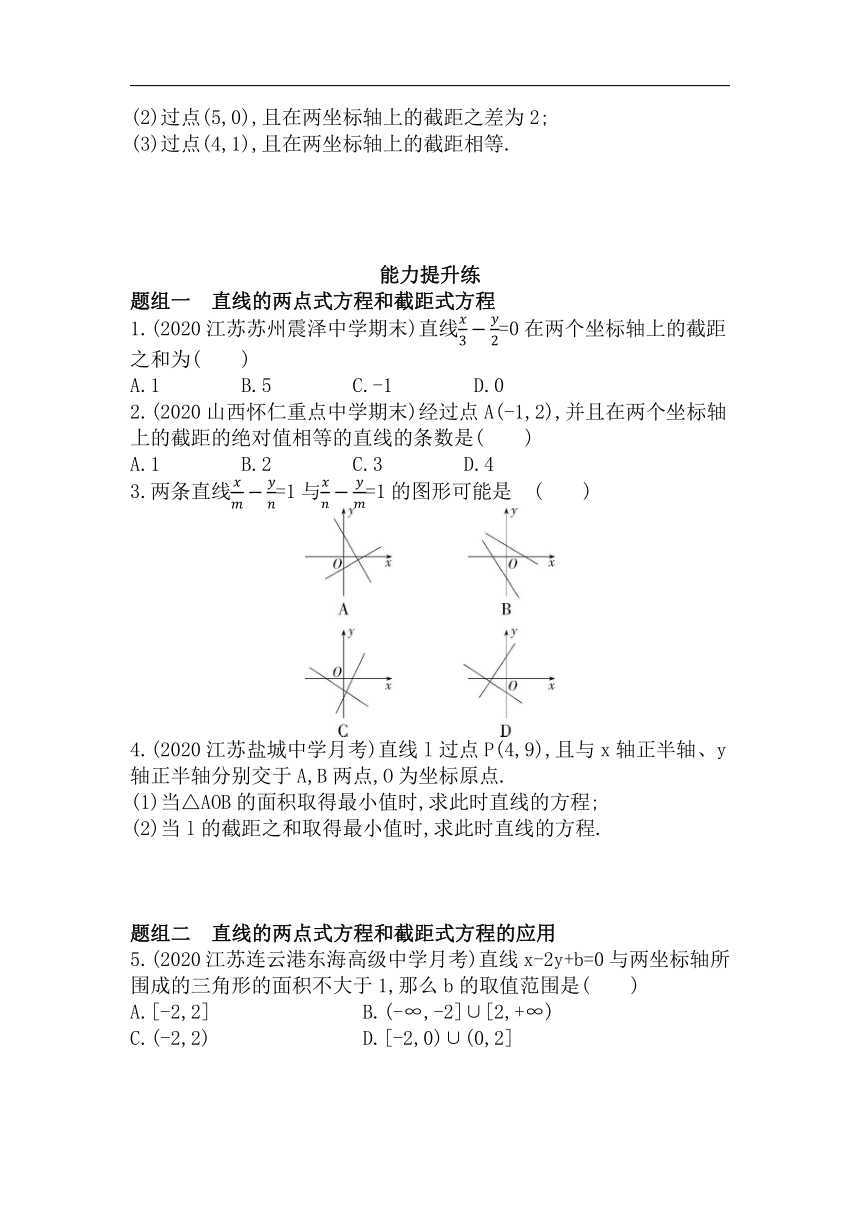
3.两条直线=1与=1的图形可能是 ( )
4.(2020江苏盐城中学月考)直线l过点P(4,9),且与x轴正半轴、y轴正半轴分别交于A,B两点,O为坐标原点.
(1)当△AOB的面积取得最小值时,求此时直线的方程;
(2)当l的截距之和取得最小值时,求此时直线的方程.
题组二 直线的两点式方程和截距式方程的应用
5.(2020江苏连云港东海高级中学月考)直线x-2y+b=0与两坐标轴所围成的三角形的面积不大于1,那么b的取值范围是( )
A.[-2,2] B.(-∞,-2]∪[2,+∞)
C.(-2,2) D.[-2,0)∪(0,2]
6.(2020江苏南京溧水高级中学期中)已知A(4,0),B(0,2),若点C(a,b)在线段AB上(不含端点),则-b的最小值为( )
A.
C.
7.(2020江苏如皋第一中学期中)已知直线l:kx+y-2k-1=0与两坐标轴分别交于A,B两点,如果△AOB的面积为4,那么满足要求的直线l的条数是( )
A.1 B.2 C.3 D.4
8.为了绿化城市,政府准备在如图所示的区域ABCDE内修建一个矩形的草坪PQRD,其中∠AED=∠EDC=∠DCB=90°,点Q在AB上,且PQ∥CD,QR⊥CD.经测量,BC=70 m,CD=80 m,DE=100 m,AE=60 m,则应如何设计才能使草坪的占地面积最大 并求出最大面积.(结果精确到1 m2)
答案全解全析
基础过关练
1.B 由直线的两点式方程,得,整理,得x+y+1=0.故选B.
2.A 由题意知直线l过点(-5,0),(3,-3),
所以l的斜率为.故选A.
3.解析 直线AB过A(4,0),B(6,7)两点,由直线的两点式方程,得,整理得7x-2y-28=0,
∴直线AB的方程为7x-2y-28=0.
直线AC过A(4,0),C(0,3)两点,由直线的两点式方程,得,整理得3x+4y-12=0,
∴直线AC的方程为3x+4y-12=0.
直线BC过B(6,7),C(0,3)两点,由直线的两点式方程,得,整理得2x-3y+9=0,
∴直线BC的方程为2x-3y+9=0.
易错警示
在应用直线的两点式方程时,要注意公式中字母或数字的顺序.
4.解析 设点A(3,2)关于x轴的对称点为A',则A'(3,-2).由已知可得反射光线所在直线为直线A'B,其方程为,即2x+y-4=0.
设点B(-1,6)关于x轴的对称点为B',则B'(-1,-6).由已知可得入射光线所在直线为直线AB',其方程为,即2x-y-4=0.
综上,入射光线所在直线的方程为2x-y-4=0,反射光线所在直线的方程为2x+y-4=0.
5.C 设直线方程为=1.由题意知a=-4,b=5,代入得=1.故选C.
6.D 直线方程可化为=1,因此,直线在x轴、y轴上的截距分别为2,-3,故选D.
7.B 因为直线过第一、三、四象限,所以它在x轴上的截距为正,在y轴上的截距为负,所以a>0,b<0.故选B.
8.解析 (1)由题易知直线在y轴上的截距为5,又直线在两坐标轴上的截距之和为2,所以直线在x轴上的截距为-3.
由直线的截距式方程,得=1,即5x-3y+15=0.
(2)由题易知直线在x轴上的截距为5,又直线在两坐标轴上的截距之差为2,所以直线在y轴上的截距为3或7.
由直线的截距式方程,得=1或=1,即3x+5y-15=0或7x+5y-35=0.
(3)①若直线在两坐标轴上的截距均不为零(即直线不过原点),
则可设直线的方程为=1,将点A的坐标(4,1)代入,得=1,解得a=5,
所以所求直线的方程为=1,即x+y-5=0.
②若直线在两坐标轴上的截距均为零(即直线过原点),
当直线的斜率存在时,可设直线的方程为y=kx,将点A的坐标(4,1)代入,得k=,
所以所求直线的方程为y=x,即x-4y=0;
当直线的斜率不存在时不满足题意.
综上,所求直线l的方程为x+y-5=0或x-4y=0.
能力提升练
1.D 令x=0,得y=0,令y=0,得x=0,所以直线=0在x轴、y轴上的截距均为0,故直线=0在两个坐标轴上的截距之和为0.故选D.
易错警示
直线的截距式方程=1的特征是x项分母对应的是直线在x轴上的截距,y项分母对应的是直线在y轴上的截距,中间以“+”连接,等式的右边为1.但是本题中的方程=0不是直线的截距式方程,因此直线在x轴上的截距不是3,在y轴上的截距也不是2.
2.C 当直线经过原点时,符合题意,易知此时直线的斜率存在,故可设直线的方程为y=kx,则2=-k,所以直线方程为y=-2x.
当直线不经过原点时,设直线方程为=1,因为点A在直线上,所以=1①,
由题知|a|=|b|,
若a=b,代入①得a=b=1,所以直线方程为x+y-1=0;
若a=-b,代入①得a=-3,b=3,所以直线方程为x-y+3=0.
综上,符合题意的直线有3条,故选C.
易错警示
在解决与两截距有关的问题时,要注意思考过原点的直线是否适合题意,防止遗漏导致错误.
3.B 直线=1在x轴、y轴上的截距分别是m,-n,直线=1在x轴、y轴上的截距分别是n,-m,因此四个截距中两正两负,对照选项中图形知B正确,故选B.
4.解析 (1)设l:=1(a>0,b>0),
∵直线l过点P(4,9),∴=1,又≥2,∴ab≥144,
则S△AOB=ab≥×144=72,当且仅当即a=8,b=18时,等号成立,
∴所求直线的方程为9x+4y-72=0.
(2)由(1)得=1,∴a+b=(a+b)≥13+2×=25,
当且仅当,即b=15,a=10时,等号成立,
此时所求直线的方程为3x+2y-30=0.
5.D 令x=0,可得y=;令y=0,可得x=-b,
∴×|-b|≤1,解得-2≤b≤2,又由题意可知b≠0,∴b的取值范围为[-2,0)∪(0,2].故选D.
6.A 由A(4,0),B(0,2)可得直线AB的方程为=1,即x+2y=4.
因为点C(a,b)在线段AB上(不含端点),所以a+2b=4(a>0,b>0).
所以≥2,
当且仅当,即a=-1时等号成立.
故选A.
7.C 当k=0时,直线l:y-1=0,不合题意;
当k≠0时,
令x=0,则y=2k+1,令y=0,则x=2+,
所以S△AOB==4,
所以4k+4+=8或4k+4+=-8,
解得k=(二重根)或k=或k=.
所以满足要求的直线l的条数是3.故选C.
8.
解析 如图,以BC边所在直线为x轴,以AE边所在直线为y轴,建立平面直角坐标系,则A(0,20),B(30,0).
所以直线AB的方程为=1,即y=20-x,
设Q(0≤x≤30),则矩形PQRD的面积S=(100-x),
即S=-x+6 000=-(x-5)2+6 000+(0≤x≤30),
易得当x=5,y=时,S取得最大值,最大值约为6 017 m2.
基础过关练
题组一 直线的两点式方程
1.(2020江苏南京雨花台中学月考)过点M(-4,3)和N(-2,1)的直线的方程是( )
A.x-y+3=0 B.x+y+1=0
C.x-y-1=0 D.x+y-3=0
2.(2020江苏苏州第六中学阶段测试)已知直线l的两点式方程为,则l的斜率为( )
A.-
3.(2020江苏张家港高级中学月考)已知三角形的三个顶点分别是A(4,0),B(6,7),C(0,3),求三边所在直线的方程.
4.一束光线从点A(3,2)发出,经x轴反射后通过点B(-1,6),分别求入射光线和反射光线所在直线的方程.
题组二 直线的截距式方程
5.(2020江苏苏州黄桥中学期中)在x轴和y轴上的截距分别为-4和5的直线的方程是 ( )
A.=1
C.=1
6.(2020吉林长春东北师大附中阶段测试)直线-=-1在x轴、y轴上的截距分别为( )
A.2,3 B.-2,3
C.-2,-3 D.2,-3
7.(2020江苏常州奔牛高级中学阶段测试)若直线=1过第一、三、四象限,则( )
A.a>0,b>0 B.a>0,b<0
C.a<0,b>0 D.a<0,b<0
8.根据下列条件求直线的方程:
(1)过点(0,5),且在两坐标轴上的截距之和为2;
(2)过点(5,0),且在两坐标轴上的截距之差为2;
(3)过点(4,1),且在两坐标轴上的截距相等.
能力提升练
题组一 直线的两点式方程和截距式方程
1.(2020江苏苏州震泽中学期末)直线=0在两个坐标轴上的截距之和为( )
A.1 B.5 C.-1 D.0
2.(2020山西怀仁重点中学期末)经过点A(-1,2),并且在两个坐标轴上的截距的绝对值相等的直线的条数是( )
A.1 B.2 C.3 D.4
3.两条直线=1与=1的图形可能是 ( )
4.(2020江苏盐城中学月考)直线l过点P(4,9),且与x轴正半轴、y轴正半轴分别交于A,B两点,O为坐标原点.
(1)当△AOB的面积取得最小值时,求此时直线的方程;
(2)当l的截距之和取得最小值时,求此时直线的方程.
题组二 直线的两点式方程和截距式方程的应用
5.(2020江苏连云港东海高级中学月考)直线x-2y+b=0与两坐标轴所围成的三角形的面积不大于1,那么b的取值范围是( )
A.[-2,2] B.(-∞,-2]∪[2,+∞)
C.(-2,2) D.[-2,0)∪(0,2]
6.(2020江苏南京溧水高级中学期中)已知A(4,0),B(0,2),若点C(a,b)在线段AB上(不含端点),则-b的最小值为( )
A.
C.
7.(2020江苏如皋第一中学期中)已知直线l:kx+y-2k-1=0与两坐标轴分别交于A,B两点,如果△AOB的面积为4,那么满足要求的直线l的条数是( )
A.1 B.2 C.3 D.4
8.为了绿化城市,政府准备在如图所示的区域ABCDE内修建一个矩形的草坪PQRD,其中∠AED=∠EDC=∠DCB=90°,点Q在AB上,且PQ∥CD,QR⊥CD.经测量,BC=70 m,CD=80 m,DE=100 m,AE=60 m,则应如何设计才能使草坪的占地面积最大 并求出最大面积.(结果精确到1 m2)
答案全解全析
基础过关练
1.B 由直线的两点式方程,得,整理,得x+y+1=0.故选B.
2.A 由题意知直线l过点(-5,0),(3,-3),
所以l的斜率为.故选A.
3.解析 直线AB过A(4,0),B(6,7)两点,由直线的两点式方程,得,整理得7x-2y-28=0,
∴直线AB的方程为7x-2y-28=0.
直线AC过A(4,0),C(0,3)两点,由直线的两点式方程,得,整理得3x+4y-12=0,
∴直线AC的方程为3x+4y-12=0.
直线BC过B(6,7),C(0,3)两点,由直线的两点式方程,得,整理得2x-3y+9=0,
∴直线BC的方程为2x-3y+9=0.
易错警示
在应用直线的两点式方程时,要注意公式中字母或数字的顺序.
4.解析 设点A(3,2)关于x轴的对称点为A',则A'(3,-2).由已知可得反射光线所在直线为直线A'B,其方程为,即2x+y-4=0.
设点B(-1,6)关于x轴的对称点为B',则B'(-1,-6).由已知可得入射光线所在直线为直线AB',其方程为,即2x-y-4=0.
综上,入射光线所在直线的方程为2x-y-4=0,反射光线所在直线的方程为2x+y-4=0.
5.C 设直线方程为=1.由题意知a=-4,b=5,代入得=1.故选C.
6.D 直线方程可化为=1,因此,直线在x轴、y轴上的截距分别为2,-3,故选D.
7.B 因为直线过第一、三、四象限,所以它在x轴上的截距为正,在y轴上的截距为负,所以a>0,b<0.故选B.
8.解析 (1)由题易知直线在y轴上的截距为5,又直线在两坐标轴上的截距之和为2,所以直线在x轴上的截距为-3.
由直线的截距式方程,得=1,即5x-3y+15=0.
(2)由题易知直线在x轴上的截距为5,又直线在两坐标轴上的截距之差为2,所以直线在y轴上的截距为3或7.
由直线的截距式方程,得=1或=1,即3x+5y-15=0或7x+5y-35=0.
(3)①若直线在两坐标轴上的截距均不为零(即直线不过原点),
则可设直线的方程为=1,将点A的坐标(4,1)代入,得=1,解得a=5,
所以所求直线的方程为=1,即x+y-5=0.
②若直线在两坐标轴上的截距均为零(即直线过原点),
当直线的斜率存在时,可设直线的方程为y=kx,将点A的坐标(4,1)代入,得k=,
所以所求直线的方程为y=x,即x-4y=0;
当直线的斜率不存在时不满足题意.
综上,所求直线l的方程为x+y-5=0或x-4y=0.
能力提升练
1.D 令x=0,得y=0,令y=0,得x=0,所以直线=0在x轴、y轴上的截距均为0,故直线=0在两个坐标轴上的截距之和为0.故选D.
易错警示
直线的截距式方程=1的特征是x项分母对应的是直线在x轴上的截距,y项分母对应的是直线在y轴上的截距,中间以“+”连接,等式的右边为1.但是本题中的方程=0不是直线的截距式方程,因此直线在x轴上的截距不是3,在y轴上的截距也不是2.
2.C 当直线经过原点时,符合题意,易知此时直线的斜率存在,故可设直线的方程为y=kx,则2=-k,所以直线方程为y=-2x.
当直线不经过原点时,设直线方程为=1,因为点A在直线上,所以=1①,
由题知|a|=|b|,
若a=b,代入①得a=b=1,所以直线方程为x+y-1=0;
若a=-b,代入①得a=-3,b=3,所以直线方程为x-y+3=0.
综上,符合题意的直线有3条,故选C.
易错警示
在解决与两截距有关的问题时,要注意思考过原点的直线是否适合题意,防止遗漏导致错误.
3.B 直线=1在x轴、y轴上的截距分别是m,-n,直线=1在x轴、y轴上的截距分别是n,-m,因此四个截距中两正两负,对照选项中图形知B正确,故选B.
4.解析 (1)设l:=1(a>0,b>0),
∵直线l过点P(4,9),∴=1,又≥2,∴ab≥144,
则S△AOB=ab≥×144=72,当且仅当即a=8,b=18时,等号成立,
∴所求直线的方程为9x+4y-72=0.
(2)由(1)得=1,∴a+b=(a+b)≥13+2×=25,
当且仅当,即b=15,a=10时,等号成立,
此时所求直线的方程为3x+2y-30=0.
5.D 令x=0,可得y=;令y=0,可得x=-b,
∴×|-b|≤1,解得-2≤b≤2,又由题意可知b≠0,∴b的取值范围为[-2,0)∪(0,2].故选D.
6.A 由A(4,0),B(0,2)可得直线AB的方程为=1,即x+2y=4.
因为点C(a,b)在线段AB上(不含端点),所以a+2b=4(a>0,b>0).
所以≥2,
当且仅当,即a=-1时等号成立.
故选A.
7.C 当k=0时,直线l:y-1=0,不合题意;
当k≠0时,
令x=0,则y=2k+1,令y=0,则x=2+,
所以S△AOB==4,
所以4k+4+=8或4k+4+=-8,
解得k=(二重根)或k=或k=.
所以满足要求的直线l的条数是3.故选C.
8.
解析 如图,以BC边所在直线为x轴,以AE边所在直线为y轴,建立平面直角坐标系,则A(0,20),B(30,0).
所以直线AB的方程为=1,即y=20-x,
设Q(0≤x≤30),则矩形PQRD的面积S=(100-x),
即S=-x+6 000=-(x-5)2+6 000+(0≤x≤30),
易得当x=5,y=时,S取得最大值,最大值约为6 017 m2.
