人教A版(2019)必修第二册《解三角形》专题9 涉角平分线 专题讲义(Word版含答案)
文档属性
| 名称 | 人教A版(2019)必修第二册《解三角形》专题9 涉角平分线 专题讲义(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 216.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 00:00:00 | ||
图片预览

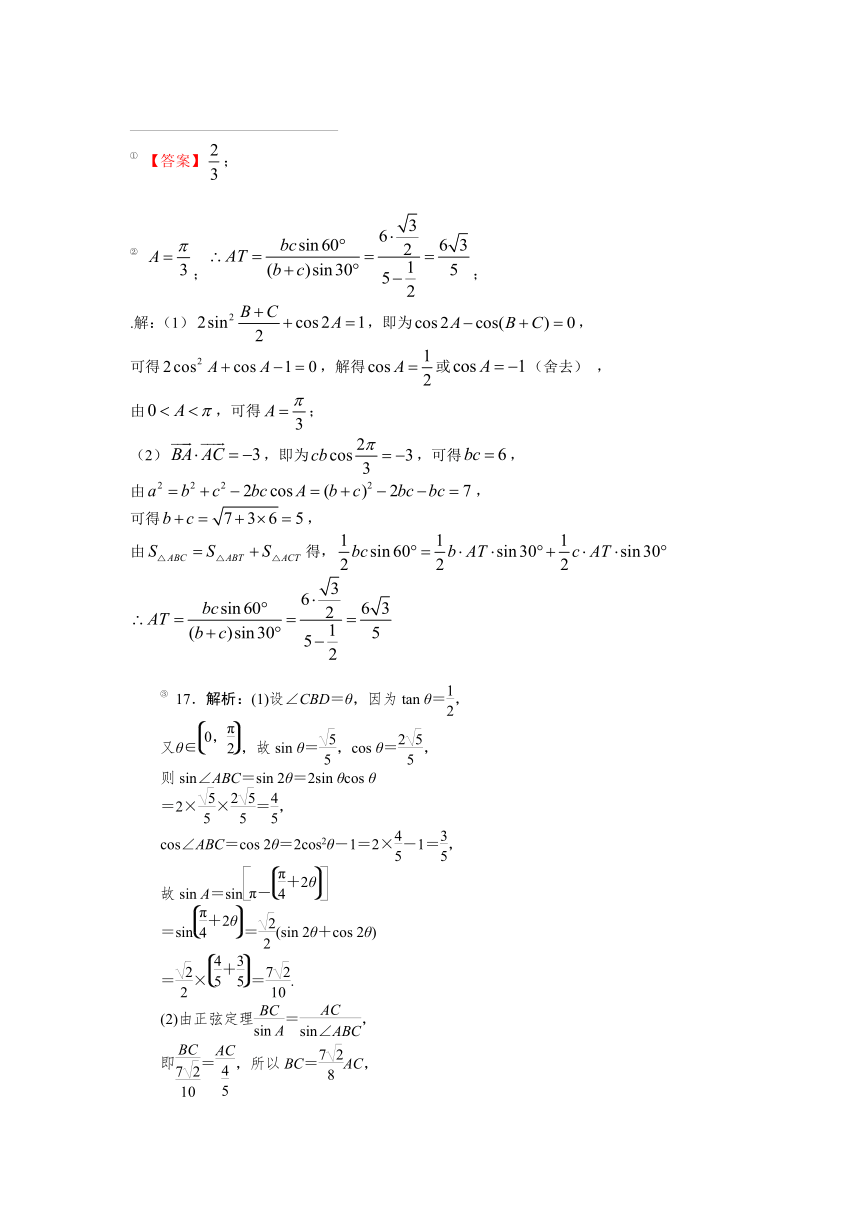
文档简介
《解三角形》专题9-1 涉角平分线
(3套2页,含答案)
知识点:
涉角平分线: 遇到三角形角平分线,一般用等面积法,即两个小三角形面积的和等于大三角形面积。
典型例题:
已知在 中, 的平分线 把三角形分成面积比为4:3的两部分,则[endnoteRef:0] .
(不用等面积法) [0: 【答案】;
]
在中,a,b,c分别为角A,B,C所对的边,且满足,
(1)求角A的大小;([endnoteRef:1])
(2)若,,的平分线交边于点T,求的长.(等面积法) [1: ;;
.解:(1),即为,
可得,解得或(舍去) ,
由,可得;
(2),即为,可得,
由,
可得,
由得,
]
随堂练习:
如图,在△ABC中,C=,∠ABC的平分线BD交AC于点D,且tan∠CBD=.
(1)求sin A;([endnoteRef:2])
(2)若·=28,求AB的长.(不用等面积法) [2: 17.解析:(1)设∠CBD=θ,因为tan θ=,
又θ∈,故sin θ=,cos θ=,
则sin∠ABC=sin 2θ=2sin θcos θ
=2××=,
cos∠ABC=cos 2θ=2cos2θ-1=2×-1=,
故sin A=sin
=sin=(sin 2θ+cos 2θ)
=×=.
(2)由正弦定理=,
即=,所以BC=AC,
又·=||||=28,
所以||||=28,所以AC=4,
又由=,得=,所以AB=5.]
在①2a-b=2ccosB,②S=(a2+b2-c2),③sin(A+B)=1+2
这三个条件中任选一个,补充在下面的横线处,然后解答问题。
在ΔABC中,角A,B,C的对边分别为a,b,c,设ΔABC的面积为S,已知 .
(1)求角C的值;([endnoteRef:3])
(2)(中档)若b=4,点D在边AB上,CD为LACB的平分线,ΔCDB的面积为,求a的值。
注:如果选择多个条件分别解答,按第一个解答计分。(等面积法) [3: 答案:(10分)
解:(1)若选①:,则由正弦定理得
,即,
∵,∴,则. …………………(4分)
若选②:,则,
化简得,∴. …………………(4分)
若选③:,则有,
化简得,所以,故. …………………(4分)
(2)在中,,
所以,
. ①
又. ②
由①②,或(舍).
. …………………(10分)
]
《解三角形》专题9-2 涉角平分线
已知△ABC的内角A, B, C的对边分别为a, b, c,且.
(Ⅰ)求角C的大小;
(Ⅱ)设角A的平分线交BC于D,且AD=,若b=,求△ABC的面积. [endnoteRef:4](不用等面积法)
[4: 答案:解: (Ⅰ)法一:由已知及余弦定理得,整理得. …2分
, ………………3分
又在△ABC中,0<C<, ………………4分
∴,即角C的大小为. .………………5分
法二:由已知及正弦定理得,
又在△ABC中,sinA=sin(B+C)=sinBcosC+cosBsinC, . ......……2分
∴2sinCcosB – sinB=2sinBcosC+2cosBsinC,
即2sinBcosC= – sinB,又sinB≠0, ………………3分
∴,又0<C<, ………………4分
∴,即角C的大小为. .………………5分
(Ⅱ)由(Ⅰ),依题意得如图,在△ADC中,AC=b=,AD=,
由正弦定理得, .………………7分
∵在△ADC中,0<<,C为钝角, ........………....………8分
∴,故. .………………9分
∵在△ABC中,AD是角A的平分线,∴, .……….……10分
∴△ABC是等腰三角形,. .………………11分
故△ABC的面积. .…………….…12分]
已知的内角所对的边分别为,.
(1);
(2)若的平分线交于点,且的面积为,求的长.[endnoteRef:5]
[5: 答案:解:(1)因为,所以.
于是,.
(2)由可得.
设的面积为,∴,
∴.则.
∵为的平分线,∴,∴.
又.∴.
在中,由余弦定理可得
,∴.
]
《解三角形》专题9-3 涉角平分线
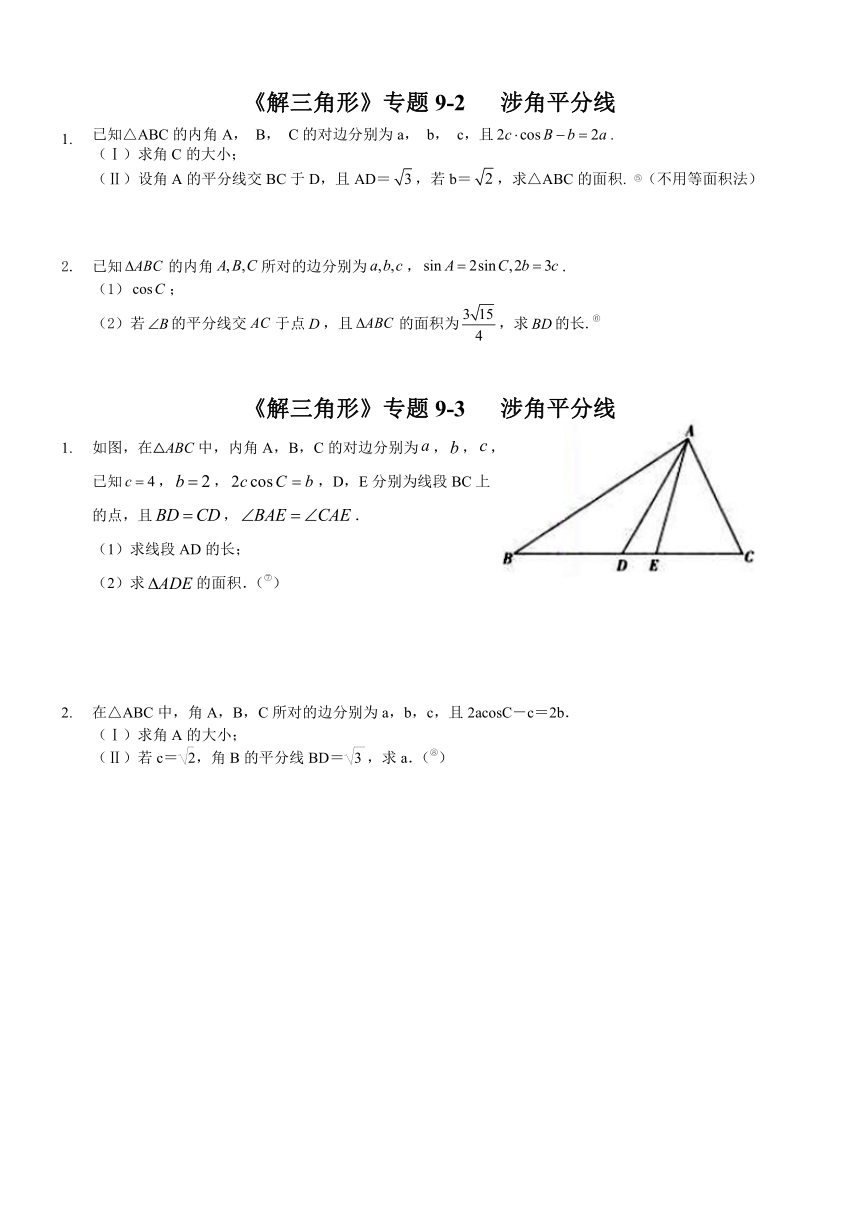
如图,在△ABC中,内角A,B,C的对边分别为,,,
已知,,,D,E分别为线段BC上
的点,且,.
(1)求线段AD的长;
(2)求的面积.([endnoteRef:6]) [6: 【解析】(1)因为,,所以.
由余弦定理得,
所以,即,
在中,,,
所以,所以.
(2)因为是的平分线,
所以,
又,所以,
所以,,
又因为,所以,
所以.
]
在△ABC中,角A,B,C所对的边分别为a,b,c,且2acosC-c=2b.
(Ⅰ)求角A的大小;
(Ⅱ)若c=,角B的平分线BD=,求a.([endnoteRef:7])
[7: 答案:(本小题满分12分)
解:(Ⅰ)2acosC-c=2b,
由正弦定理得 2sinAcosC-sinC=2sinB, …2分
2sinAcosC-sinC=2sin(A+C) =2sinAcosC+2cosAsinC,
∴-sinC=2cosAsinC,
∵sinC≠0,∴cosA=-,
而A∈(0, π),∴A=. …6分
(Ⅱ)在△ABD中,由正弦定理得,=
∴ sin∠ADB==,
∴ ∠ADB=, …9分
∴∠ABC=,∠ACB=,AC=AB=
由余弦定理, BC==. …12分]
(3套2页,含答案)
知识点:
涉角平分线: 遇到三角形角平分线,一般用等面积法,即两个小三角形面积的和等于大三角形面积。
典型例题:
已知在 中, 的平分线 把三角形分成面积比为4:3的两部分,则[endnoteRef:0] .
(不用等面积法) [0: 【答案】;
]
在中,a,b,c分别为角A,B,C所对的边,且满足,
(1)求角A的大小;([endnoteRef:1])
(2)若,,的平分线交边于点T,求的长.(等面积法) [1: ;;
.解:(1),即为,
可得,解得或(舍去) ,
由,可得;
(2),即为,可得,
由,
可得,
由得,
]
随堂练习:
如图,在△ABC中,C=,∠ABC的平分线BD交AC于点D,且tan∠CBD=.
(1)求sin A;([endnoteRef:2])
(2)若·=28,求AB的长.(不用等面积法) [2: 17.解析:(1)设∠CBD=θ,因为tan θ=,
又θ∈,故sin θ=,cos θ=,
则sin∠ABC=sin 2θ=2sin θcos θ
=2××=,
cos∠ABC=cos 2θ=2cos2θ-1=2×-1=,
故sin A=sin
=sin=(sin 2θ+cos 2θ)
=×=.
(2)由正弦定理=,
即=,所以BC=AC,
又·=||||=28,
所以||||=28,所以AC=4,
又由=,得=,所以AB=5.]
在①2a-b=2ccosB,②S=(a2+b2-c2),③sin(A+B)=1+2
这三个条件中任选一个,补充在下面的横线处,然后解答问题。
在ΔABC中,角A,B,C的对边分别为a,b,c,设ΔABC的面积为S,已知 .
(1)求角C的值;([endnoteRef:3])
(2)(中档)若b=4,点D在边AB上,CD为LACB的平分线,ΔCDB的面积为,求a的值。
注:如果选择多个条件分别解答,按第一个解答计分。(等面积法) [3: 答案:(10分)
解:(1)若选①:,则由正弦定理得
,即,
∵,∴,则. …………………(4分)
若选②:,则,
化简得,∴. …………………(4分)
若选③:,则有,
化简得,所以,故. …………………(4分)
(2)在中,,
所以,
. ①
又. ②
由①②,或(舍).
. …………………(10分)
]
《解三角形》专题9-2 涉角平分线
已知△ABC的内角A, B, C的对边分别为a, b, c,且.
(Ⅰ)求角C的大小;
(Ⅱ)设角A的平分线交BC于D,且AD=,若b=,求△ABC的面积. [endnoteRef:4](不用等面积法)
[4: 答案:解: (Ⅰ)法一:由已知及余弦定理得,整理得. …2分
, ………………3分
又在△ABC中,0<C<, ………………4分
∴,即角C的大小为. .………………5分
法二:由已知及正弦定理得,
又在△ABC中,sinA=sin(B+C)=sinBcosC+cosBsinC, . ......……2分
∴2sinCcosB – sinB=2sinBcosC+2cosBsinC,
即2sinBcosC= – sinB,又sinB≠0, ………………3分
∴,又0<C<, ………………4分
∴,即角C的大小为. .………………5分
(Ⅱ)由(Ⅰ),依题意得如图,在△ADC中,AC=b=,AD=,
由正弦定理得, .………………7分
∵在△ADC中,0<<,C为钝角, ........………....………8分
∴,故. .………………9分
∵在△ABC中,AD是角A的平分线,∴, .……….……10分
∴△ABC是等腰三角形,. .………………11分
故△ABC的面积. .…………….…12分]
已知的内角所对的边分别为,.
(1);
(2)若的平分线交于点,且的面积为,求的长.[endnoteRef:5]
[5: 答案:解:(1)因为,所以.
于是,.
(2)由可得.
设的面积为,∴,
∴.则.
∵为的平分线,∴,∴.
又.∴.
在中,由余弦定理可得
,∴.
]
《解三角形》专题9-3 涉角平分线
如图,在△ABC中,内角A,B,C的对边分别为,,,
已知,,,D,E分别为线段BC上
的点,且,.
(1)求线段AD的长;
(2)求的面积.([endnoteRef:6]) [6: 【解析】(1)因为,,所以.
由余弦定理得,
所以,即,
在中,,,
所以,所以.
(2)因为是的平分线,
所以,
又,所以,
所以,,
又因为,所以,
所以.
]
在△ABC中,角A,B,C所对的边分别为a,b,c,且2acosC-c=2b.
(Ⅰ)求角A的大小;
(Ⅱ)若c=,角B的平分线BD=,求a.([endnoteRef:7])
[7: 答案:(本小题满分12分)
解:(Ⅰ)2acosC-c=2b,
由正弦定理得 2sinAcosC-sinC=2sinB, …2分
2sinAcosC-sinC=2sin(A+C) =2sinAcosC+2cosAsinC,
∴-sinC=2cosAsinC,
∵sinC≠0,∴cosA=-,
而A∈(0, π),∴A=. …6分
(Ⅱ)在△ABD中,由正弦定理得,=
∴ sin∠ADB==,
∴ ∠ADB=, …9分
∴∠ABC=,∠ACB=,AC=AB=
由余弦定理, BC==. …12分]
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
