人教A版(2019)选择性必修第三册《随机变量》专题3 用排列组合算分布列 学案(Word版含答案)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册《随机变量》专题3 用排列组合算分布列 学案(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 465.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 00:00:00 | ||
图片预览




文档简介
《随机变量》专题3-1 用排列组合算分布列
(5套6页,含答案)
知识点:
随机变量——用排列组合来算分布列: (又称作:超几何分布) 一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品数,则事件{X=k}发生的概率为,k=0,1,2,…,m,其中m=min{M,n},且n≤N,M≤N,
n、M、N∈N*,称分布列为 超几何分布列. 如果随机变量X的分布列为超几何分布列,则称随机变量X 服从超几何分布 .
典型例题:
设一个口袋中装有10个球其中红球2个,绿球3个,白球5个,这三种球除颜色外完全相同.从中一次任意选取3个,取后不放回.
(1)求三种颜色球各取到1个的概率;
(2)设X表示取到的红球的个数,求X的分布列与数学期望.
(答案:[endnoteRef:0];;;) [0: (本小题满分12分)
解:(1)设表示事件“三种颜色的球各取到一个”……2分
则……6分
(2)X的所有可能值为0,1,2……7分
且
X的分布列为
……10分
(个) ……12分
]
随堂练习:
某大学志愿者协会有6名男同学,4名女同学.在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院.现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(Ⅰ)求选出的3名同学是来自互不相同学院的概率;
(Ⅱ)设X为选出的3名同学中女同学的人数,求随机变量X的分布列和数学期望.([endnoteRef:1])
答案:,
; [1: 解:(Ⅰ)设“选出的3名同学是来自互不相同的学院”为事件A,则
P(A)==.
所以,选出的3名同学是来自互不相同学院的概率为.……………4分
(Ⅱ)随机变量X的所有可能值为0,1,2,3.
P(X=k)=(k=0,1,2,3).
∴P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==. …………………8分
所以,随机变量X的分布列是
……………………10分
随机变量X的数学期望E(X)=0×+1×+2×+3×=. ……12分]
为了解甲、乙两个班级某次考试的数学成绩(单位:分) ,从甲、乙两个班级中分别随机抽取5名学生的成绩作样本,如图是样本的茎叶图.
规定:成绩不低于120分时为优秀成绩.
(1)从甲班的样本中随机抽取 2 个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名同学的成绩,记获优秀成绩的人数为 ,
求的分布列和数学期望E.([endnoteRef:2]) [2: 解:(1) ……3分
(2)的所有可能取值为0,1,2,3 ……4分
,
……8分
的分布列为
……10分
的数学期望为 ……12分
]
每年5月到7月,是芒果的成熟季节,某大学校内也种植了很多食用芒果。据该校后勤处负责人介绍,他们校内的芒果种植过程中没有使用过农药,也没有路边那种绿化芒的污染,可以放心食用。2018年该校的芒果也迎来了大丰收。6月25日,该校南北校区集中采摘芒果,并将采摘到的芒果免费派送给学校师生。现随机从一些芒果树上摘下100个芒果,其质量分别在[100,150), [150,200), [200,250),(单位:克)中,
经统计得频率分布直方图如图所示.
(Ⅰ)现按分层抽样从质量为的芒果中随机抽取9个,再从这9个中随机抽取3个,记随机变量X表示质量在内的芒果个数,求X的分布列及数学期望.
(Ⅱ)以各组数据的中间数代表这组数据的平均值,将频率视为概率,假如你是经销商去收购芒果,该校当时还未摘下的芒果大约还有10000个,现提供如下两种收购方案:
A:所有芒果以10元/千克收购;
B:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购.
通过计算确定你会选择哪种方案?([endnoteRef:3]) [3: 19.(Ⅰ)9个芒果中,质量在内的分别有6个和3个.
则的可能取值为0,1,2,3.
………………………4分
所以的分布列为
X的数学期望
. ………………………6分
(Ⅱ)方案A:
………………………9分
方案B:
低于克:(0.002+0.002+0.003)×50×10000×2=7000(元)
高于或等于250克(0.008+0.004+0.001)×50×10000×3=19500(元)
总计7000+19500=26500元
由25750<26500,故B方案支出更多,应选A方案. ………………………12分
]
《随机变量》专题3-2 用排列组合算分布列(基础)
在含有3件次品的100件产品中,任取2件,求:
(Ⅰ)取到的次品数X的分布列(分布列中的概率值用分数表示,不能含组合符号);
(Ⅱ)至少取到1件次品的概率.([endnoteRef:4])
答案:
,;
[4: 答案:(Ⅰ)因为从100件产品中任取2件的结果数为,从100件产品中任取2件其中恰有k件次品的结果数为,所以从100件产品中任取2件,其中恰有k件次品的概率为---------------------------------------4分
---------------------------------------------------------------8分
(Ⅱ)根据随机变量X的分布列,可得至少取到1件次品的概率为
---------------------------------------12分]
如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为,据此解答如下问题.
(Ⅰ)求全班人数及分数在之间的频率;
(Ⅱ)现从分数在之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在的份数为 ,求的分布列和数学期望.([endnoteRef:5] )
答案:频率为,
;
[5: 答案:(Ⅰ)由茎叶图知分数在的人数为4人;的人数为8人;的人数为10人.
总人数为………………………………….3分
分数在人数为人频率为…….5分
(Ⅱ)的人数为6人;分数在的人数为4人
的取值可能为0,1,2,3
…………………10分
分布列为
………………………………….12分]
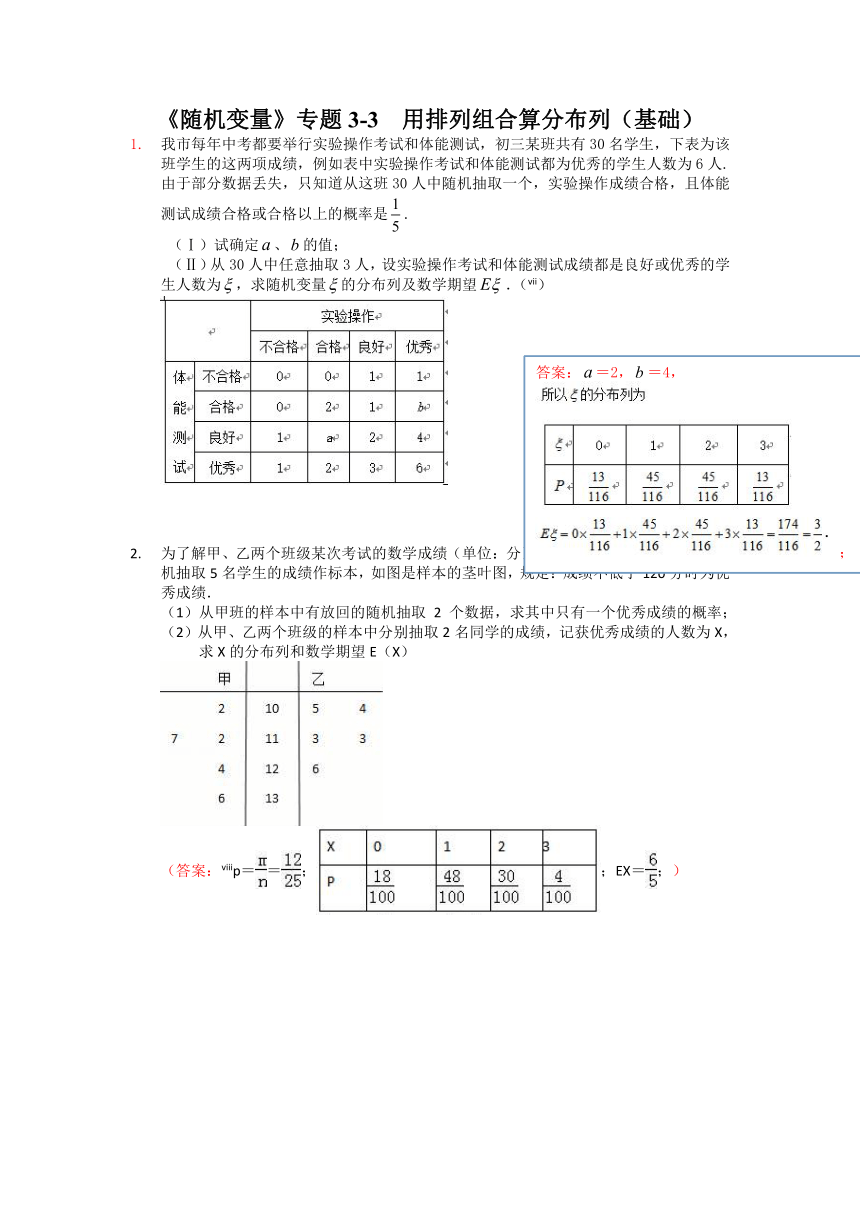
《随机变量》专题3-3 用排列组合算分布列(基础)
我市每年中考都要举行实验操作考试和体能测试,初三某班共有30名学生,下表为该班学生的这两项成绩,例如表中实验操作考试和体能测试都为优秀的学生人数为6人.由于部分数据丢失,只知道从这班30人中随机抽取一个,实验操作成绩合格,且体能测试成绩合格或合格以上的概率是.
(Ⅰ)试确定、的值;
(Ⅱ)从30人中任意抽取3人,设实验操作考试和体能测试成绩都是良好或优秀的学生人数为,求随机变量的分布列及数学期望.([endnoteRef:6])
[6: 答案:(Ⅰ)由表格数据可知,实验操作成绩合格、且体能测试成绩合格或合格以上的学生共有人,记“实验操作成绩合格、且体能测试成绩合格或合格以上”为事件,则,解得,所以.
答:的值为2,的值为4. ………………………4分
(Ⅱ)由于从30位学生中任意抽取3位的结果数为,其中实验操作考试和体能测试成绩都是良好或优秀的学生人数为15人,从30人中任意抽取3人,其中恰有个实验操作考试和体能测试成绩都是良好或优秀的结果数为,所以从30人中任意抽取3人,其中恰有人实验操作考试和体能测试成绩都是良好或优秀的的概率
为,,的可能取值为,
则,,
,, …………………………8分
所以的分布列为
. …………………12分]
为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作标本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩.
(1)从甲班的样本中有放回的随机抽取 2 个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名同学的成绩,记获优秀成绩的人数为X,
求X的分布列和数学期望E(X)
(答案:[endnoteRef:7]p==;;EX=;) [7: 【考点】离散型随机变量的期望与方差;茎叶图.
【专题】概率与统计.
【分析】(1)甲班抽取的5名学生的成绩为102,112,117,124,136,从中有放回地抽取两个数据,基本事件总数n=52=25,其中只有一个优秀成绩,包含的基本事件个数m=2×3+3×2=12,由此利用等可能事件概率计算公式能求出其中只有一个优秀成绩的概率.
(2)由茎叶图知甲班抽取的5名学生中有2名学生成绩优秀,乙班抽取的5名学生中有1名学生成绩优秀,由此得X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望E(X).
【解答】解:(1)甲班抽取的5名学生的成绩为102,112,117,124,136,
从中有放回地抽取两个数据,基本事件总数n=52=25,
其中只有一个优秀成绩,包含的基本事件个数m=2×3+3×2=12,
∴其中只有一个优秀成绩的概率p==.
(2)由茎叶图知甲班抽取的5名学生中有2名学生成绩优秀,
乙班抽取的5名学生中有1名学生成绩优秀,
由此得X的可能取值为0,1,2,3,
P(X=0)==,
P(X=1)=+=,
P(X=2)=+=,
P(X=3)==,
∴X的分布列为:
EX==.
【点评】本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合知识的合理运用.
]
《随机变量》专题3-4 用排列组合算分布列(中下)
一个袋中有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球,得到黑球的概率是;从袋中任意摸出2个球,至少得到1个白球的概率是.
(Ⅰ)若袋中共有10个球,
(i)求白球的个数;
(ii)从袋中任意摸出3个球,记得到白球的个数为,求随机变量的数学期望.
(Ⅱ)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于.并指出袋中哪种颜色的球个数最少.
(答案:[endnoteRef:8]5个;;期望;;红球最少;) [8:
9、解:(Ⅰ)(i)记“从袋中任意摸出两个球,至少得到一个白球”为事件A,
设袋中白球的个数为,则,………………………2分
得到.故白球有5个.………………………3分
(ii)随机变量的取值为0,1,2,3,分布列是………………………4分
………………………6分
注解:(每算对2各给1分)
的数学期望
.………………………8分
(Ⅱ)证明:设袋中有个球,其中个黑球,由题意得,
所以,,故.………9分
记“从袋中任意摸出两个球,至少有1个黑球”为事件B,则
.………11分
所以白球的个数比黑球多,白球个数多于,红球的个数少于.
故袋中红球个数最少.………12分
]
调查表明:甲种农作物的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为x,y,z,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标ω=x+y+z的值评定这种农作物的长势等级,若ω≥4,则长势为一级;若2≤ω≤3,则长势为二级;若0≤ω≤1,则长势为三级,为了了解目前这种农作物长势情况,研究人员随机抽取10块种植地,得到如下表中结果:
(Ⅰ)在这10块该农作物的种植地中任取两块地,求这两块地的空气湿度的指标z相同的概率;
(Ⅱ)从长势等级是一级的种植地中任取一块地,其综合指标为A,从长势等级不是一级的种植地中任取一块地,其综合指标为B,记随机变量X=A-B,求X的分布列及其数学期望. ([endnoteRef:9])
答案:概率
;
[9: (Ⅰ)由表可知:空气湿度指标为1的有A2, A4,A5,A7, A9,A10 ………1分
空气湿度指标为2的有A1,A3,A6,A8, …………………………………………2分
在这10块种植地中任取两块地,基本事件总数n= ………………3分
这两块地的空气温度的指标z相同包含的基本事件个数 ……………………………………………………5分
∴这两地的空气温度的指标z相同的概率 ………………………6分
(Ⅱ)由题意得10块种植地的综合指标如下表:
其中长势等级是一级(ω≥4)有A1 , A2,A3,A5, A6,A8, A9,共7个,
长势等级不是一级(ω<4)的有A4, A7, A10,共3个, ………………………………7分
随机变量X=A-B的所有可能取值为1, 2,3,4, 5, ………………………………8分
w=4的有A1 , A2,A5, A6,A9共5块地,w=3的有A7, A10共2块地,这时有X=4﹣3=1
所以, …………………………………………………………9分
同理 ,
, ……………………………10分
∴X的分布列为:
…………………………………………………………………………………………… 11分 ]
《随机变量》专题3-5 用排列组合算分布列(中下)
某学校为了解该校高三年级学生数学科学习情况,对广一模考试数学成绩进行分析,从中抽取了n 名学生的成绩作为样本进行统计(该校全体学生的成绩均在[60,140) ,按照[60,70),[70,80),[80,90),[90,100),[100,110),[110,120),[120,130),[130,140)的分组作出频率分布直方图如图(a)所示,样本中分数在[70,90)内的所有数据的茎叶图如图(b)所示.
根据上级统计划出预录分数线,有下列分数与可能被录取院校层次对照表为表( c ).
(Ⅰ)求n和频率分布直方图中的x, y的值;
(Ⅱ)根据样本估计总体的思想,以事件发生的频率作为概率,若在该校高三年级学生中任取3 人,求至少有一人是可能录取为重本层次院校的概率;
(Ⅲ)在选取的样本中,从可能录取为重本和专科两个层次的学生中随机抽取3 名学生进行调研,用表示所抽取的3 名学生中为重本的人数,求随机变量的分布列和数学期望.([endnoteRef:10])
答案:x=0.01,y=0.014,,
;
[10: 答案:解:(1)由题意可知,样本容量 …………1分
…………2分
…………3分
(2)成绩能被重点大学录取的人数为人, 抽取的人中成绩能被重点大学录取的频率是,故从该校高三年级学生中任取人的概率为 …………4分
记该校高三年级学生中任取人,至少有一人能被重点大学录取的事件为;
则 …………5分
(3)成绩能被重点大学录取的人数为人,成绩能被专科学校录取的人数为人, …………6分
故随机变量的所有可能取值为 …………7分
所以,,,, …………9分
故随机变量的分布列为
…………11分
随机变量的数学期望 …………12分]
(5套6页,含答案)
知识点:
随机变量——用排列组合来算分布列: (又称作:超几何分布) 一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品数,则事件{X=k}发生的概率为,k=0,1,2,…,m,其中m=min{M,n},且n≤N,M≤N,
n、M、N∈N*,称分布列为 超几何分布列. 如果随机变量X的分布列为超几何分布列,则称随机变量X 服从超几何分布 .
典型例题:
设一个口袋中装有10个球其中红球2个,绿球3个,白球5个,这三种球除颜色外完全相同.从中一次任意选取3个,取后不放回.
(1)求三种颜色球各取到1个的概率;
(2)设X表示取到的红球的个数,求X的分布列与数学期望.
(答案:[endnoteRef:0];;;) [0: (本小题满分12分)
解:(1)设表示事件“三种颜色的球各取到一个”……2分
则……6分
(2)X的所有可能值为0,1,2……7分
且
X的分布列为
……10分
(个) ……12分
]
随堂练习:
某大学志愿者协会有6名男同学,4名女同学.在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院.现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(Ⅰ)求选出的3名同学是来自互不相同学院的概率;
(Ⅱ)设X为选出的3名同学中女同学的人数,求随机变量X的分布列和数学期望.([endnoteRef:1])
答案:,
; [1: 解:(Ⅰ)设“选出的3名同学是来自互不相同的学院”为事件A,则
P(A)==.
所以,选出的3名同学是来自互不相同学院的概率为.……………4分
(Ⅱ)随机变量X的所有可能值为0,1,2,3.
P(X=k)=(k=0,1,2,3).
∴P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==. …………………8分
所以,随机变量X的分布列是
……………………10分
随机变量X的数学期望E(X)=0×+1×+2×+3×=. ……12分]
为了解甲、乙两个班级某次考试的数学成绩(单位:分) ,从甲、乙两个班级中分别随机抽取5名学生的成绩作样本,如图是样本的茎叶图.
规定:成绩不低于120分时为优秀成绩.
(1)从甲班的样本中随机抽取 2 个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名同学的成绩,记获优秀成绩的人数为 ,
求的分布列和数学期望E.([endnoteRef:2]) [2: 解:(1) ……3分
(2)的所有可能取值为0,1,2,3 ……4分
,
……8分
的分布列为
……10分
的数学期望为 ……12分
]
每年5月到7月,是芒果的成熟季节,某大学校内也种植了很多食用芒果。据该校后勤处负责人介绍,他们校内的芒果种植过程中没有使用过农药,也没有路边那种绿化芒的污染,可以放心食用。2018年该校的芒果也迎来了大丰收。6月25日,该校南北校区集中采摘芒果,并将采摘到的芒果免费派送给学校师生。现随机从一些芒果树上摘下100个芒果,其质量分别在[100,150), [150,200), [200,250),(单位:克)中,
经统计得频率分布直方图如图所示.
(Ⅰ)现按分层抽样从质量为的芒果中随机抽取9个,再从这9个中随机抽取3个,记随机变量X表示质量在内的芒果个数,求X的分布列及数学期望.
(Ⅱ)以各组数据的中间数代表这组数据的平均值,将频率视为概率,假如你是经销商去收购芒果,该校当时还未摘下的芒果大约还有10000个,现提供如下两种收购方案:
A:所有芒果以10元/千克收购;
B:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购.
通过计算确定你会选择哪种方案?([endnoteRef:3]) [3: 19.(Ⅰ)9个芒果中,质量在内的分别有6个和3个.
则的可能取值为0,1,2,3.
………………………4分
所以的分布列为
X的数学期望
. ………………………6分
(Ⅱ)方案A:
………………………9分
方案B:
低于克:(0.002+0.002+0.003)×50×10000×2=7000(元)
高于或等于250克(0.008+0.004+0.001)×50×10000×3=19500(元)
总计7000+19500=26500元
由25750<26500,故B方案支出更多,应选A方案. ………………………12分
]
《随机变量》专题3-2 用排列组合算分布列(基础)
在含有3件次品的100件产品中,任取2件,求:
(Ⅰ)取到的次品数X的分布列(分布列中的概率值用分数表示,不能含组合符号);
(Ⅱ)至少取到1件次品的概率.([endnoteRef:4])
答案:
,;
[4: 答案:(Ⅰ)因为从100件产品中任取2件的结果数为,从100件产品中任取2件其中恰有k件次品的结果数为,所以从100件产品中任取2件,其中恰有k件次品的概率为---------------------------------------4分
---------------------------------------------------------------8分
(Ⅱ)根据随机变量X的分布列,可得至少取到1件次品的概率为
---------------------------------------12分]
如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为,据此解答如下问题.
(Ⅰ)求全班人数及分数在之间的频率;
(Ⅱ)现从分数在之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在的份数为 ,求的分布列和数学期望.([endnoteRef:5] )
答案:频率为,
;
[5: 答案:(Ⅰ)由茎叶图知分数在的人数为4人;的人数为8人;的人数为10人.
总人数为………………………………….3分
分数在人数为人频率为…….5分
(Ⅱ)的人数为6人;分数在的人数为4人
的取值可能为0,1,2,3
…………………10分
分布列为
………………………………….12分]
《随机变量》专题3-3 用排列组合算分布列(基础)
我市每年中考都要举行实验操作考试和体能测试,初三某班共有30名学生,下表为该班学生的这两项成绩,例如表中实验操作考试和体能测试都为优秀的学生人数为6人.由于部分数据丢失,只知道从这班30人中随机抽取一个,实验操作成绩合格,且体能测试成绩合格或合格以上的概率是.
(Ⅰ)试确定、的值;
(Ⅱ)从30人中任意抽取3人,设实验操作考试和体能测试成绩都是良好或优秀的学生人数为,求随机变量的分布列及数学期望.([endnoteRef:6])
[6: 答案:(Ⅰ)由表格数据可知,实验操作成绩合格、且体能测试成绩合格或合格以上的学生共有人,记“实验操作成绩合格、且体能测试成绩合格或合格以上”为事件,则,解得,所以.
答:的值为2,的值为4. ………………………4分
(Ⅱ)由于从30位学生中任意抽取3位的结果数为,其中实验操作考试和体能测试成绩都是良好或优秀的学生人数为15人,从30人中任意抽取3人,其中恰有个实验操作考试和体能测试成绩都是良好或优秀的结果数为,所以从30人中任意抽取3人,其中恰有人实验操作考试和体能测试成绩都是良好或优秀的的概率
为,,的可能取值为,
则,,
,, …………………………8分
所以的分布列为
. …………………12分]
为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作标本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩.
(1)从甲班的样本中有放回的随机抽取 2 个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名同学的成绩,记获优秀成绩的人数为X,
求X的分布列和数学期望E(X)
(答案:[endnoteRef:7]p==;;EX=;) [7: 【考点】离散型随机变量的期望与方差;茎叶图.
【专题】概率与统计.
【分析】(1)甲班抽取的5名学生的成绩为102,112,117,124,136,从中有放回地抽取两个数据,基本事件总数n=52=25,其中只有一个优秀成绩,包含的基本事件个数m=2×3+3×2=12,由此利用等可能事件概率计算公式能求出其中只有一个优秀成绩的概率.
(2)由茎叶图知甲班抽取的5名学生中有2名学生成绩优秀,乙班抽取的5名学生中有1名学生成绩优秀,由此得X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望E(X).
【解答】解:(1)甲班抽取的5名学生的成绩为102,112,117,124,136,
从中有放回地抽取两个数据,基本事件总数n=52=25,
其中只有一个优秀成绩,包含的基本事件个数m=2×3+3×2=12,
∴其中只有一个优秀成绩的概率p==.
(2)由茎叶图知甲班抽取的5名学生中有2名学生成绩优秀,
乙班抽取的5名学生中有1名学生成绩优秀,
由此得X的可能取值为0,1,2,3,
P(X=0)==,
P(X=1)=+=,
P(X=2)=+=,
P(X=3)==,
∴X的分布列为:
EX==.
【点评】本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合知识的合理运用.
]
《随机变量》专题3-4 用排列组合算分布列(中下)
一个袋中有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球,得到黑球的概率是;从袋中任意摸出2个球,至少得到1个白球的概率是.
(Ⅰ)若袋中共有10个球,
(i)求白球的个数;
(ii)从袋中任意摸出3个球,记得到白球的个数为,求随机变量的数学期望.
(Ⅱ)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于.并指出袋中哪种颜色的球个数最少.
(答案:[endnoteRef:8]5个;;期望;;红球最少;) [8:
9、解:(Ⅰ)(i)记“从袋中任意摸出两个球,至少得到一个白球”为事件A,
设袋中白球的个数为,则,………………………2分
得到.故白球有5个.………………………3分
(ii)随机变量的取值为0,1,2,3,分布列是………………………4分
………………………6分
注解:(每算对2各给1分)
的数学期望
.………………………8分
(Ⅱ)证明:设袋中有个球,其中个黑球,由题意得,
所以,,故.………9分
记“从袋中任意摸出两个球,至少有1个黑球”为事件B,则
.………11分
所以白球的个数比黑球多,白球个数多于,红球的个数少于.
故袋中红球个数最少.………12分
]
调查表明:甲种农作物的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为x,y,z,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标ω=x+y+z的值评定这种农作物的长势等级,若ω≥4,则长势为一级;若2≤ω≤3,则长势为二级;若0≤ω≤1,则长势为三级,为了了解目前这种农作物长势情况,研究人员随机抽取10块种植地,得到如下表中结果:
(Ⅰ)在这10块该农作物的种植地中任取两块地,求这两块地的空气湿度的指标z相同的概率;
(Ⅱ)从长势等级是一级的种植地中任取一块地,其综合指标为A,从长势等级不是一级的种植地中任取一块地,其综合指标为B,记随机变量X=A-B,求X的分布列及其数学期望. ([endnoteRef:9])
答案:概率
;
[9: (Ⅰ)由表可知:空气湿度指标为1的有A2, A4,A5,A7, A9,A10 ………1分
空气湿度指标为2的有A1,A3,A6,A8, …………………………………………2分
在这10块种植地中任取两块地,基本事件总数n= ………………3分
这两块地的空气温度的指标z相同包含的基本事件个数 ……………………………………………………5分
∴这两地的空气温度的指标z相同的概率 ………………………6分
(Ⅱ)由题意得10块种植地的综合指标如下表:
其中长势等级是一级(ω≥4)有A1 , A2,A3,A5, A6,A8, A9,共7个,
长势等级不是一级(ω<4)的有A4, A7, A10,共3个, ………………………………7分
随机变量X=A-B的所有可能取值为1, 2,3,4, 5, ………………………………8分
w=4的有A1 , A2,A5, A6,A9共5块地,w=3的有A7, A10共2块地,这时有X=4﹣3=1
所以, …………………………………………………………9分
同理 ,
, ……………………………10分
∴X的分布列为:
…………………………………………………………………………………………… 11分 ]
《随机变量》专题3-5 用排列组合算分布列(中下)
某学校为了解该校高三年级学生数学科学习情况,对广一模考试数学成绩进行分析,从中抽取了n 名学生的成绩作为样本进行统计(该校全体学生的成绩均在[60,140) ,按照[60,70),[70,80),[80,90),[90,100),[100,110),[110,120),[120,130),[130,140)的分组作出频率分布直方图如图(a)所示,样本中分数在[70,90)内的所有数据的茎叶图如图(b)所示.
根据上级统计划出预录分数线,有下列分数与可能被录取院校层次对照表为表( c ).
(Ⅰ)求n和频率分布直方图中的x, y的值;
(Ⅱ)根据样本估计总体的思想,以事件发生的频率作为概率,若在该校高三年级学生中任取3 人,求至少有一人是可能录取为重本层次院校的概率;
(Ⅲ)在选取的样本中,从可能录取为重本和专科两个层次的学生中随机抽取3 名学生进行调研,用表示所抽取的3 名学生中为重本的人数,求随机变量的分布列和数学期望.([endnoteRef:10])
答案:x=0.01,y=0.014,,
;
[10: 答案:解:(1)由题意可知,样本容量 …………1分
…………2分
…………3分
(2)成绩能被重点大学录取的人数为人, 抽取的人中成绩能被重点大学录取的频率是,故从该校高三年级学生中任取人的概率为 …………4分
记该校高三年级学生中任取人,至少有一人能被重点大学录取的事件为;
则 …………5分
(3)成绩能被重点大学录取的人数为人,成绩能被专科学校录取的人数为人, …………6分
故随机变量的所有可能取值为 …………7分
所以,,,, …………9分
故随机变量的分布列为
…………11分
随机变量的数学期望 …………12分]
