人教版数学七年级下册5.1~5.2 滚动训练课课练(word版含答案)
文档属性
| 名称 | 人教版数学七年级下册5.1~5.2 滚动训练课课练(word版含答案) | 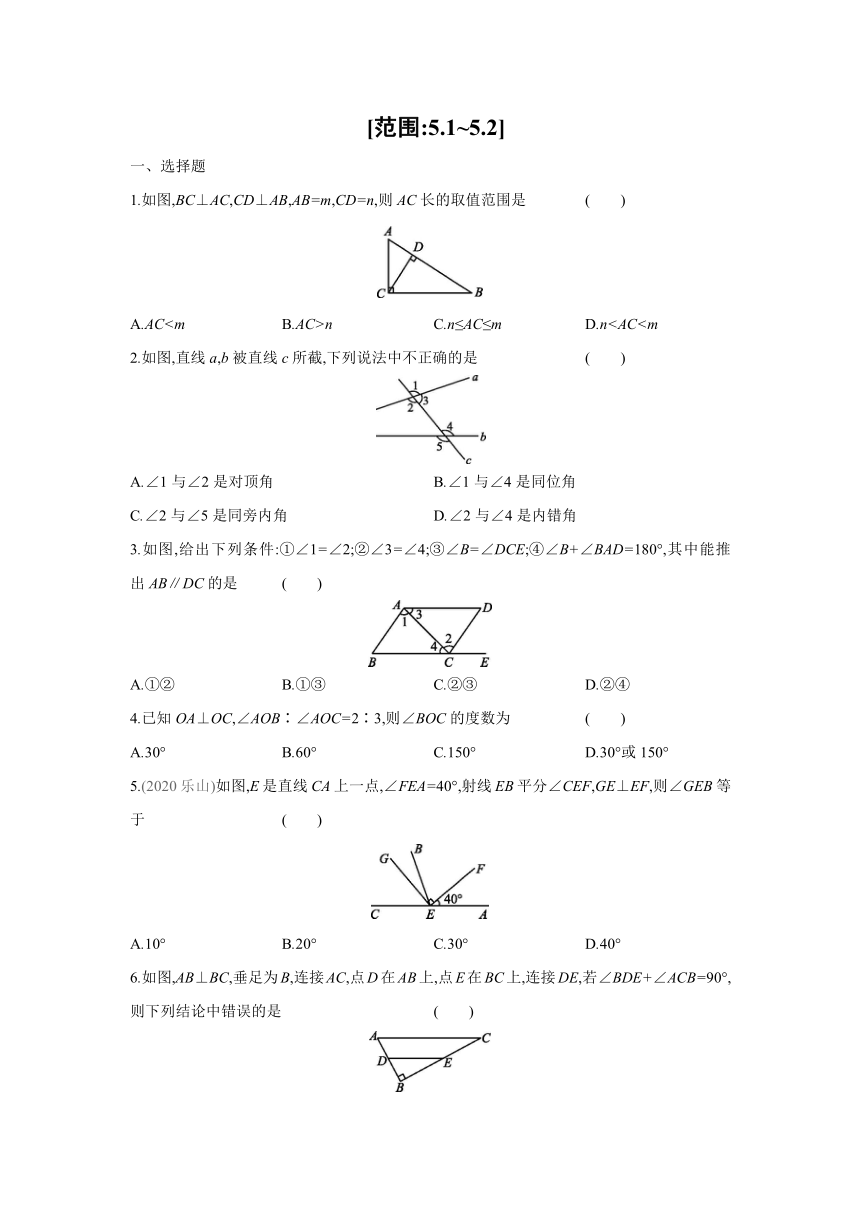 | |
| 格式 | docx | ||
| 文件大小 | 192.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 15:20:38 | ||
图片预览

文档简介
[范围:5.1~5.2]
一、选择题
1.如图,BC⊥AC,CD⊥AB,AB=m,CD=n,则AC长的取值范围是 ( )
A.ACn C.n≤AC≤m D.n2.如图,直线a,b被直线c所截,下列说法中不正确的是 ( )
A.∠1与∠2是对顶角 B.∠1与∠4是同位角
C.∠2与∠5是同旁内角 D.∠2与∠4是内错角
3.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出AB∥DC的是 ( )
A.①② B.①③ C.②③ D.②④
4.已知OA⊥OC,∠AOB∶∠AOC=2∶3,则∠BOC的度数为 ( )
A.30° B.60° C.150° D.30°或150°
5.(2020乐山)如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF,则∠GEB等于 ( )
A.10° B.20° C.30° D.40°
6.如图,AB⊥BC,垂足为B,连接AC,点D在AB上,点E在BC上,连接DE,若∠BDE+∠ACB=90°,则下列结论中错误的是 ( )
A.AC∥DE B.∠BDE=∠BAC
C.∠BAC+∠BED=90° D.∠BDE+∠BAC=∠BED+∠BCA
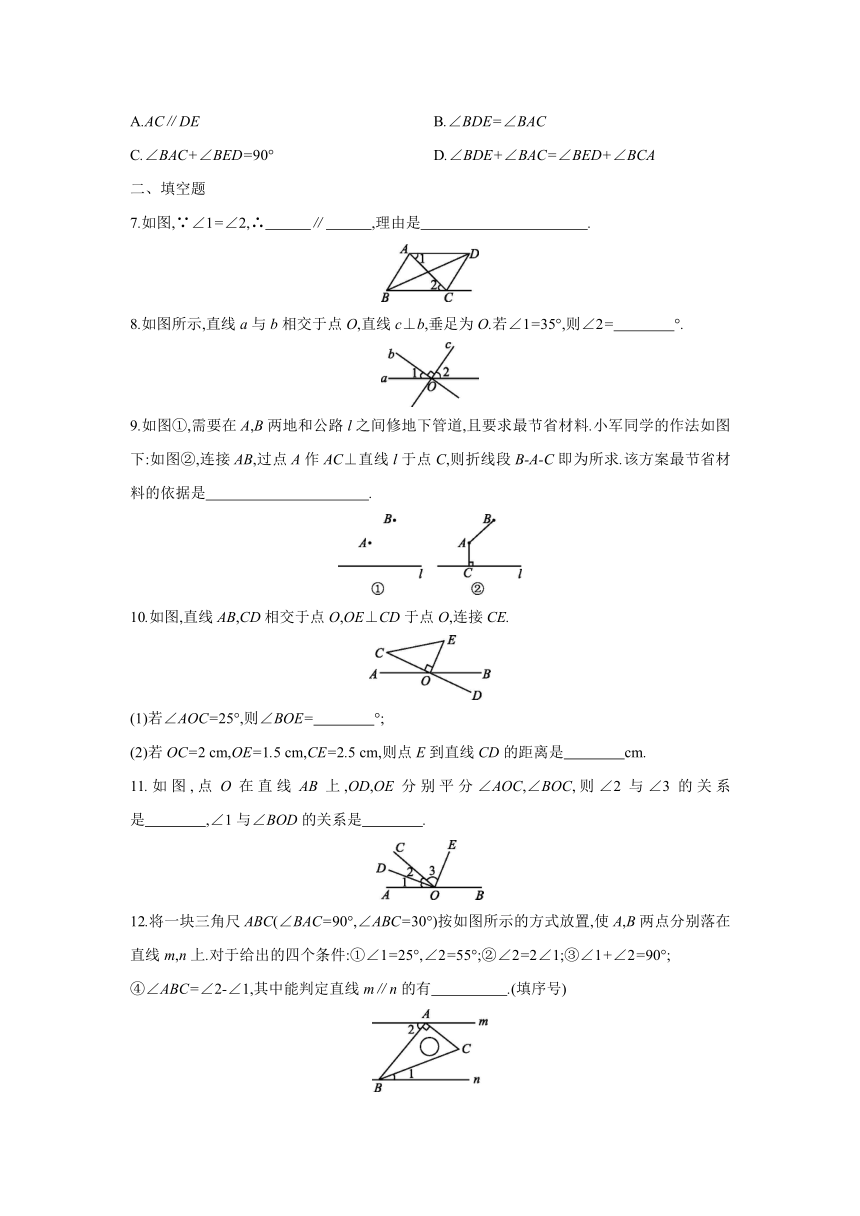
二、填空题
7.如图,∵∠1=∠2,∴ ∥ ,理由是 .
8.如图所示,直线a与b相交于点O,直线c⊥b,垂足为O.若∠1=35°,则∠2= °.
9.如图①,需要在A,B两地和公路l之间修地下管道,且要求最节省材料.小军同学的作法如图下:如图②,连接AB,过点A作AC⊥直线l于点C,则折线段B-A-C即为所求.该方案最节省材料的依据是 .
10.如图,直线AB,CD相交于点O,OE⊥CD于点O,连接CE.
(1)若∠AOC=25°,则∠BOE= °;
(2)若OC=2 cm,OE=1.5 cm,CE=2.5 cm,则点E到直线CD的距离是 cm.
11.如图,点O在直线AB上,OD,OE分别平分∠AOC,∠BOC,则∠2与∠3的关系是 ,∠1与∠BOD的关系是 .
12.将一块三角尺ABC(∠BAC=90°,∠ABC=30°)按如图所示的方式放置,使A,B两点分别落在直线m,n上.对于给出的四个条件:①∠1=25°,∠2=55°;②∠2=2∠1;③∠1+∠2=90°;
④∠ABC=∠2-∠1,其中能判定直线m∥n的有 .(填序号)
三、解答题
13.如图,已知点F在AB上,∠1和∠D互余,CF⊥DF,则AB与CD平行吗 为什么
14.如图,AB⊥BC,BC⊥CD,且∠1=∠2.试说明:BE∥CF.
15.如图,已知点E在BD上,AE⊥CE,EC平分∠DEF.
(1)试说明:EA平分∠BEF;
(2)若∠1=∠A,∠2=∠C,试说明:AB∥CD.
答案
1.D 2.C 3.B
4.D
因为OA⊥OC,所以∠AOC=90°.因为∠AOB∶∠AOC=2∶3,所以∠AOB=60°.∠AOB的位置有两种情况:一种是在∠AOC内,一种是在∠AOC外.如图,①当∠AOB在∠AOC内时,∠BOC=90°-60°=30°;②当∠AOB在∠AOC外时,∠BOC=90°+60°=150°.故选D.
5.B ∵∠FEA=40°,∴∠CEF=180°-40°=140°.
∵射线EB平分∠CEF,∴∠BEF=×140°=70°.
∵GE⊥EF,∴∠GEF=90°,∴∠GEB=90°-70°=20°.故选B.
6.D
7.AD BC 内错角相等,两直线平行
8.55 ∵直线a与b相交于点O,直线c⊥b,垂足为O,∠1=35°,∴∠2=180°-90°-35°=55°.
9.两点之间,线段最短;垂线段最短
10.(1)65 (2)1.5 (1)∵OE⊥CD,
∴∠COE=90°.
又∵∠AOC=25°,
∴∠BOE=180°-90°-25°=65°.
(2)∵OE⊥CD于点O,OE=1.5 cm,
∴点E到直线CD的距离是1.5 cm.
11.互余 互补 12.①④
13.解:AB∥CD.理由如图下:
∵CF⊥DF,
∴∠CFD=90°.
∵∠1+∠CFD+∠BFD=180°,
∴∠1+∠BFD=90°.
∵∠1和∠D互余,
∴∠1+∠D=90°,
∴∠BFD=∠D,
∴AB∥CD.
14.解:∵AB⊥BC,BC⊥CD(已知),
∴∠ABC=∠BCD=90°(垂直的定义).
又∵∠1=∠2(已知),
∴∠ABC-∠1=∠BCD-∠2(等式的性质),
即∠EBC=∠FCB,
∴BE∥CF(内错角相等,两直线平行).
15.解:(1)如图,∵AE⊥CE,∴∠AEC=90°,
∴∠3+∠4=90°,∠1+∠2=90°.
∵EC平分∠DEF,∴∠2=∠4,
∴∠1=∠3,∴EA平分∠BEF.
(2)如图,由(1)知∠1=∠3,∠2=∠4.
∵∠2=∠C,
∴∠4=∠C,∴EF∥CD.
∵∠1=∠A,∴∠3=∠A,
∴EF∥AB,∴AB∥CD.
一、选择题
1.如图,BC⊥AC,CD⊥AB,AB=m,CD=n,则AC长的取值范围是 ( )
A.AC
A.∠1与∠2是对顶角 B.∠1与∠4是同位角
C.∠2与∠5是同旁内角 D.∠2与∠4是内错角
3.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出AB∥DC的是 ( )
A.①② B.①③ C.②③ D.②④
4.已知OA⊥OC,∠AOB∶∠AOC=2∶3,则∠BOC的度数为 ( )
A.30° B.60° C.150° D.30°或150°
5.(2020乐山)如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF,则∠GEB等于 ( )
A.10° B.20° C.30° D.40°
6.如图,AB⊥BC,垂足为B,连接AC,点D在AB上,点E在BC上,连接DE,若∠BDE+∠ACB=90°,则下列结论中错误的是 ( )
A.AC∥DE B.∠BDE=∠BAC
C.∠BAC+∠BED=90° D.∠BDE+∠BAC=∠BED+∠BCA
二、填空题
7.如图,∵∠1=∠2,∴ ∥ ,理由是 .
8.如图所示,直线a与b相交于点O,直线c⊥b,垂足为O.若∠1=35°,则∠2= °.
9.如图①,需要在A,B两地和公路l之间修地下管道,且要求最节省材料.小军同学的作法如图下:如图②,连接AB,过点A作AC⊥直线l于点C,则折线段B-A-C即为所求.该方案最节省材料的依据是 .
10.如图,直线AB,CD相交于点O,OE⊥CD于点O,连接CE.
(1)若∠AOC=25°,则∠BOE= °;
(2)若OC=2 cm,OE=1.5 cm,CE=2.5 cm,则点E到直线CD的距离是 cm.
11.如图,点O在直线AB上,OD,OE分别平分∠AOC,∠BOC,则∠2与∠3的关系是 ,∠1与∠BOD的关系是 .
12.将一块三角尺ABC(∠BAC=90°,∠ABC=30°)按如图所示的方式放置,使A,B两点分别落在直线m,n上.对于给出的四个条件:①∠1=25°,∠2=55°;②∠2=2∠1;③∠1+∠2=90°;
④∠ABC=∠2-∠1,其中能判定直线m∥n的有 .(填序号)
三、解答题
13.如图,已知点F在AB上,∠1和∠D互余,CF⊥DF,则AB与CD平行吗 为什么
14.如图,AB⊥BC,BC⊥CD,且∠1=∠2.试说明:BE∥CF.
15.如图,已知点E在BD上,AE⊥CE,EC平分∠DEF.
(1)试说明:EA平分∠BEF;
(2)若∠1=∠A,∠2=∠C,试说明:AB∥CD.
答案
1.D 2.C 3.B
4.D
因为OA⊥OC,所以∠AOC=90°.因为∠AOB∶∠AOC=2∶3,所以∠AOB=60°.∠AOB的位置有两种情况:一种是在∠AOC内,一种是在∠AOC外.如图,①当∠AOB在∠AOC内时,∠BOC=90°-60°=30°;②当∠AOB在∠AOC外时,∠BOC=90°+60°=150°.故选D.
5.B ∵∠FEA=40°,∴∠CEF=180°-40°=140°.
∵射线EB平分∠CEF,∴∠BEF=×140°=70°.
∵GE⊥EF,∴∠GEF=90°,∴∠GEB=90°-70°=20°.故选B.
6.D
7.AD BC 内错角相等,两直线平行
8.55 ∵直线a与b相交于点O,直线c⊥b,垂足为O,∠1=35°,∴∠2=180°-90°-35°=55°.
9.两点之间,线段最短;垂线段最短
10.(1)65 (2)1.5 (1)∵OE⊥CD,
∴∠COE=90°.
又∵∠AOC=25°,
∴∠BOE=180°-90°-25°=65°.
(2)∵OE⊥CD于点O,OE=1.5 cm,
∴点E到直线CD的距离是1.5 cm.
11.互余 互补 12.①④
13.解:AB∥CD.理由如图下:
∵CF⊥DF,
∴∠CFD=90°.
∵∠1+∠CFD+∠BFD=180°,
∴∠1+∠BFD=90°.
∵∠1和∠D互余,
∴∠1+∠D=90°,
∴∠BFD=∠D,
∴AB∥CD.
14.解:∵AB⊥BC,BC⊥CD(已知),
∴∠ABC=∠BCD=90°(垂直的定义).
又∵∠1=∠2(已知),
∴∠ABC-∠1=∠BCD-∠2(等式的性质),
即∠EBC=∠FCB,
∴BE∥CF(内错角相等,两直线平行).
15.解:(1)如图,∵AE⊥CE,∴∠AEC=90°,
∴∠3+∠4=90°,∠1+∠2=90°.
∵EC平分∠DEF,∴∠2=∠4,
∴∠1=∠3,∴EA平分∠BEF.
(2)如图,由(1)知∠1=∠3,∠2=∠4.
∵∠2=∠C,
∴∠4=∠C,∴EF∥CD.
∵∠1=∠A,∴∠3=∠A,
∴EF∥AB,∴AB∥CD.
