人教版九年级上册21.2.1配方法课件 (共16张PPT)
文档属性
| 名称 | 人教版九年级上册21.2.1配方法课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 241.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 12:13:59 | ||
图片预览




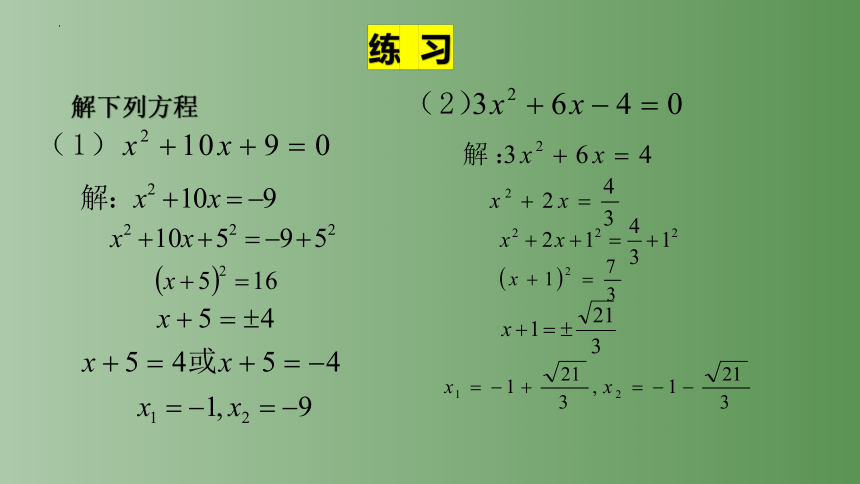

文档简介
(共16张PPT)
人教版 九年级上册
第21章 一元二次方程
21.2.2 一元二次方程的解法---配方法(2)
1.会用配方法解一元二次方程.
2.能说出用配方法解一元二次方程的基本步骤.
3.通过用配方法将一元二次方程变形的过程,让学生进
一步体会转化的思想方法,并增强他们的数学应用意识和能力.
学习目标
知识回顾
解方程:
用配方法解方程 2x2-3x+1=0
解:两边都除以2,得
移项,得
配方,得
开方,得
∴
二次项系数化为1
常数项右移变号
配方
开方
定解
变形
写成两个一元一次方程
新知探究
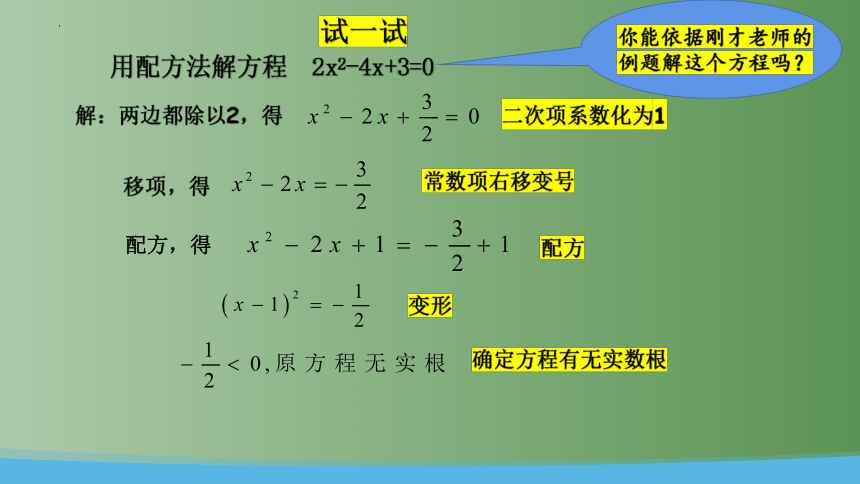
用配方法解方程 2x2-4x+3=0
解:两边都除以2,得
移项,得
配方,得
二次项系数化为1
常数项右移变号
配方
变形
试一试
确定方程有无实数根
你能依据刚才老师的例题解这个方程吗?
练 习
解下列方程
配方法解一元二次方程的基本思路:
1.二次项系数化为1
2.常数项右移变号
3.两边同时加上一次项系数一半的平方
4.将方程化为(x+m)2=n的形式
5.讨论:当n≥0时,方程有两个实数根.开方求解
当n<0时,方程无实数根.
归 纳
例:已知x2+y2-6x+2y+10=0,x、y为实数,
则x= ,y= .
配方法的应用
解:∵x2+y2-6x+2y+10=0
∴x2-6x+y2+2y+10=0
x2-6x+9+y2+2y+1=0
(x-3)2+(y+1)2=0
∴x=3,y=-1
练:已知m,n是等腰△ABC的腰和底,且满足m2+n2-6m-8n+25=0,则△ABC的周长为 .
配方法的应用
解:∵m2+n2-6m-8n+25=0
∴m2-6m+n2-8n+25=0
m2-6m+9+n2-8n+16=0
(m-3)2+(n-4)2=0
∴m=3,n=4
周长为3+3+4=10或4+4+3=11
小明认为代数式x2-6x+15的值不小于6.你认为他说的对吗?是说明理由
解:x2-6x+15
=x2-6x+9-9+15
=(x-3)2+6,
∵(x-3)2≥0
∴(x-3)2+6≥6.
所以代数式x2-6x+12的值不小于6.小明说的对
配方法的应用
1. 方程 可以化成 ,进行降次,
得 ,方程的根为 .
课堂检测
2.用配方法解一元二次方程ax2+bx+c=0时,首先把二次项系数化成 ,然后方程的两边同时加上 项系数 的 .
1
一次
一半
平方
课堂检测
4.用配方法解方程x2-2x-3=0时,配方后所得的方程为 ( )
A.(x+1)2=4 B.(x-1)2=2
C.(x+1)2=-2 D.(x-1)2=4
D
3.用配方法解一元二次方程,将x2-6x+2=0化成(x+a)2=b的形式,
则a,b的值分别是 ( )
A.-3, -11 B. 3, -11 C.3, 7 D.-3,7
D
5.用配方法解方程 ,则方程可变形为 ( )
D
课堂检测
6.用配方法解方程
(x-4)2=13
解:3x2-6x=-5
课堂检测
此方程无实数解
7.已知m2+n2-4m-8n+20=0,m+n= .
解:∵m2+n2-4m-8n+20=0
∴m2-4m+n2-8n+20=0
m2-4m+4+n2-8n+16=0
(m-2)2+(n-4)2=0
∴m=2,n=4
m+n=6
课堂检测
坚持就是胜利!
人教版 九年级上册
第21章 一元二次方程
21.2.2 一元二次方程的解法---配方法(2)
1.会用配方法解一元二次方程.
2.能说出用配方法解一元二次方程的基本步骤.
3.通过用配方法将一元二次方程变形的过程,让学生进
一步体会转化的思想方法,并增强他们的数学应用意识和能力.
学习目标
知识回顾
解方程:
用配方法解方程 2x2-3x+1=0
解:两边都除以2,得
移项,得
配方,得
开方,得
∴
二次项系数化为1
常数项右移变号
配方
开方
定解
变形
写成两个一元一次方程
新知探究
用配方法解方程 2x2-4x+3=0
解:两边都除以2,得
移项,得
配方,得
二次项系数化为1
常数项右移变号
配方
变形
试一试
确定方程有无实数根
你能依据刚才老师的例题解这个方程吗?
练 习
解下列方程
配方法解一元二次方程的基本思路:
1.二次项系数化为1
2.常数项右移变号
3.两边同时加上一次项系数一半的平方
4.将方程化为(x+m)2=n的形式
5.讨论:当n≥0时,方程有两个实数根.开方求解
当n<0时,方程无实数根.
归 纳
例:已知x2+y2-6x+2y+10=0,x、y为实数,
则x= ,y= .
配方法的应用
解:∵x2+y2-6x+2y+10=0
∴x2-6x+y2+2y+10=0
x2-6x+9+y2+2y+1=0
(x-3)2+(y+1)2=0
∴x=3,y=-1
练:已知m,n是等腰△ABC的腰和底,且满足m2+n2-6m-8n+25=0,则△ABC的周长为 .
配方法的应用
解:∵m2+n2-6m-8n+25=0
∴m2-6m+n2-8n+25=0
m2-6m+9+n2-8n+16=0
(m-3)2+(n-4)2=0
∴m=3,n=4
周长为3+3+4=10或4+4+3=11
小明认为代数式x2-6x+15的值不小于6.你认为他说的对吗?是说明理由
解:x2-6x+15
=x2-6x+9-9+15
=(x-3)2+6,
∵(x-3)2≥0
∴(x-3)2+6≥6.
所以代数式x2-6x+12的值不小于6.小明说的对
配方法的应用
1. 方程 可以化成 ,进行降次,
得 ,方程的根为 .
课堂检测
2.用配方法解一元二次方程ax2+bx+c=0时,首先把二次项系数化成 ,然后方程的两边同时加上 项系数 的 .
1
一次
一半
平方
课堂检测
4.用配方法解方程x2-2x-3=0时,配方后所得的方程为 ( )
A.(x+1)2=4 B.(x-1)2=2
C.(x+1)2=-2 D.(x-1)2=4
D
3.用配方法解一元二次方程,将x2-6x+2=0化成(x+a)2=b的形式,
则a,b的值分别是 ( )
A.-3, -11 B. 3, -11 C.3, 7 D.-3,7
D
5.用配方法解方程 ,则方程可变形为 ( )
D
课堂检测
6.用配方法解方程
(x-4)2=13
解:3x2-6x=-5
课堂检测
此方程无实数解
7.已知m2+n2-4m-8n+20=0,m+n= .
解:∵m2+n2-4m-8n+20=0
∴m2-4m+n2-8n+20=0
m2-4m+4+n2-8n+16=0
(m-2)2+(n-4)2=0
∴m=2,n=4
m+n=6
课堂检测
坚持就是胜利!
同课章节目录
